Quadratic forms, reduction of
The isolation of "reduced" forms in each class of quadratic forms over a given ring 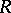 , i.e. of (one or several) "standard" forms in the class. The main aim of the reduction of quadratic forms is the solution of the problem of equivalence of quadratic forms: To establish whether or not two given quadratic forms
, i.e. of (one or several) "standard" forms in the class. The main aim of the reduction of quadratic forms is the solution of the problem of equivalence of quadratic forms: To establish whether or not two given quadratic forms 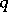 and
and  are equivalent over
are equivalent over 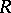 , and in the case of their equivalence to find (or describe) all the invertible matrices
, and in the case of their equivalence to find (or describe) all the invertible matrices 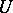 over
over 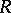 taking
taking 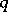 to
to  (see Quadratic form). For the solution of the latter problem it suffices to know just one such matrix
(see Quadratic form). For the solution of the latter problem it suffices to know just one such matrix 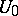 and all the automorphisms
and all the automorphisms 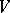 of the form
of the form 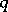 , since then
, since then 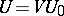 . One usually has in mind equivalence of quadratic forms over
. One usually has in mind equivalence of quadratic forms over 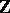 , where one is often considering the entire collection of quadratic forms over
, where one is often considering the entire collection of quadratic forms over 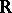 and their classes over
and their classes over 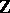 . There are fundamental differences in the reduction theory of positive-definite and indefinite quadratic forms.
. There are fundamental differences in the reduction theory of positive-definite and indefinite quadratic forms.
The reduction of positive-definite quadratic forms.
There are different methods for the reduction over 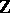 of real positive-definite quadratic forms. Of these the most extensive and widely studied is the Minkowski (or Hermite–Minkowski) reduction method. The most general method is Venkov's method. Other prevalent reductions are those of E. Selling
of real positive-definite quadratic forms. Of these the most extensive and widely studied is the Minkowski (or Hermite–Minkowski) reduction method. The most general method is Venkov's method. Other prevalent reductions are those of E. Selling 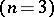 and H.F. Charve
and H.F. Charve 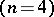 .
.
To determine a reduced quadratic form
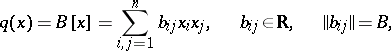 |
means to define in the positivity cone 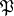 of the coefficient space
of the coefficient space 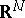 ,
, 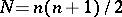 , a domain of reduction
, a domain of reduction 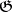 such that
such that 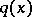 is reduced if and only if
is reduced if and only if 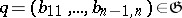 . It is desirable that
. It is desirable that 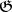 possesses good geometric properties (such as simple connectedness, convexity, etc.) and is a fundamental domain of the group
possesses good geometric properties (such as simple connectedness, convexity, etc.) and is a fundamental domain of the group 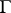 of integer transformations of determinant
of integer transformations of determinant 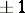 . A domain
. A domain 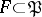 is called a fundamental domain of reduction of positive-definite quadratic forms if
is called a fundamental domain of reduction of positive-definite quadratic forms if 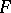 is an open domain in
is an open domain in 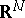 and if: 1) for each
and if: 1) for each 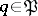 there is an equivalent quadratic form
there is an equivalent quadratic form 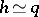 (
(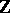 ) for which
) for which 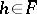 ; and 2) if
; and 2) if 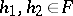 and
and 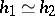 (
(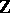 ), then
), then 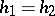 .
.
a) Minkowski reduction of a quadratic form. A positive-definite quadratic form 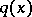 is Minkowski reduced if for any
is Minkowski reduced if for any 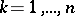 and any integers
and any integers 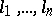 with greatest common divisor
with greatest common divisor 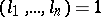 ,
,
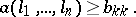 | (1) |
From the infinite number of inequalities (1) for the coefficients 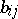 one can extract a finite number such that the remaining inequalities follow from them. In the coefficient space
one can extract a finite number such that the remaining inequalities follow from them. In the coefficient space 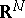 the set of Minkowski-reduced forms is an infinite complex pyramid (a gonohedron) with a finite number of faces, called the domain of Minkowski reduction (or Hermite–Minkowski gonohedron)
the set of Minkowski-reduced forms is an infinite complex pyramid (a gonohedron) with a finite number of faces, called the domain of Minkowski reduction (or Hermite–Minkowski gonohedron) 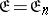 ;
; 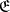 is a closed set,
is a closed set, 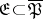 . For
. For 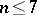 the faces of
the faces of 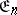 have been calculated (see ).
have been calculated (see ).
There exists a constant 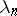 such that if the quadratic form
such that if the quadratic form 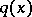 is Minkowski reduced, then
is Minkowski reduced, then
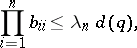 |
where 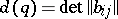 is the determinant of
is the determinant of 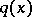 .
.
Each real positive-definite quadratic form is equivalent over 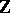 to a Minkowski-reduced quadratic form. There is an algorithm for the reduction (for finding a reduced form that is equivalent to a given one) (see [8], [15]).
to a Minkowski-reduced quadratic form. There is an algorithm for the reduction (for finding a reduced form that is equivalent to a given one) (see [8], [15]).
For 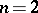 ,
, 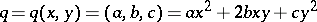 ,
, 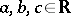 ,
, 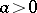 ,
, 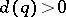 , the conditions of being reduced have the form
, the conditions of being reduced have the form
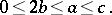 |
If one restricts oneself to proper equivalence (when only integer-valued transformations with determinant 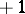 are admitted), then the domain of reduction has the form
are admitted), then the domain of reduction has the form 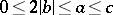 (the Lagrange–Gauss reduction conditions). The set of all inequivalent (properly-) reduced quadratic forms can be written as the union
(the Lagrange–Gauss reduction conditions). The set of all inequivalent (properly-) reduced quadratic forms can be written as the union 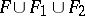 , where
, where
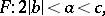 |
 |
For 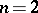 there is an algorithm for Gauss reduction, according to which one has to go over from a form not satisfying the Lagrange–Gauss conditions to its "neighbour" ,
there is an algorithm for Gauss reduction, according to which one has to go over from a form not satisfying the Lagrange–Gauss conditions to its "neighbour" ,
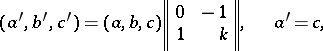 |
where the integer 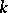 is chosen such that
is chosen such that 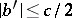 . For any real quadratic form
. For any real quadratic form 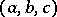 the algorithm is broken up into a finite number of steps.
the algorithm is broken up into a finite number of steps.
If 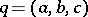 ,
, 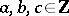 , with greatest common divisor
, with greatest common divisor 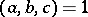 , then for
, then for 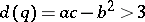 there are only two automorphisms (of determinant 1); for
there are only two automorphisms (of determinant 1); for 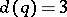 , six automorphisms; and for
, six automorphisms; and for 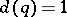 , four automorphisms.
, four automorphisms.
b) Venkov reduction of a quadratic form. This is a reduction method 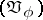 , depending on a parameter
, depending on a parameter 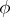 , for an arbitrary real positive-definite
, for an arbitrary real positive-definite  -ary quadratic form
-ary quadratic form 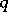 (see [3]). A quadratic form
(see [3]). A quadratic form 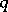 is said to be
is said to be 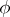 -reducible if
-reducible if
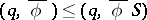 |
for all integer-valued 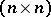 -matrices
-matrices 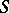 of determinant 1; here
of determinant 1; here 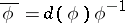 is the form reciprocal to
is the form reciprocal to 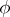 ,
, 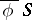 is the quadratic form obtained from
is the quadratic form obtained from 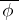 by the transformation
by the transformation 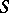 , and
, and 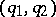 is the Voronoi semi-invariant, defined as follows: if
is the Voronoi semi-invariant, defined as follows: if 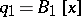 ,
, 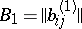 ,
, 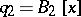 ,
, 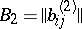 , then
, then
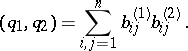 |
The set of 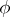 -reducible quadratic forms in the coefficient space
-reducible quadratic forms in the coefficient space 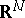 is a convex gonohedron
is a convex gonohedron 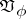 with a finite number of faces lying in
with a finite number of faces lying in 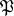 . If
. If 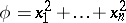 and
and 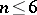 , then
, then 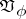 is the same as the domain of Minkowski reduction.
is the same as the domain of Minkowski reduction.
c) Selling and Charve reduction of a quadratic form. If in the Venkov reduction one puts 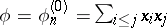 , where
, where 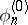 is the Voronoi first perfect form, then for
is the Voronoi first perfect form, then for 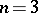 one obtains the Selling reduction, and for
one obtains the Selling reduction, and for 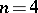 the Charve reduction (see , [6]).
the Charve reduction (see , [6]).
The reduction of indefinite quadratic forms.
This is in principle more complicated than that of positive quadratic forms. There are no fundamental domains for them. Only for 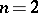 is there a definitive reduction theory of quadratic forms over
is there a definitive reduction theory of quadratic forms over 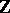 .
.
a) Reduction of indefinite binary quadratic forms. Let
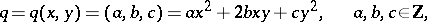 |
be a quadratic form with determinant 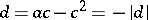 , where
, where 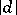 is not a perfect square. Associated with
is not a perfect square. Associated with 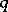 is the quadratic equation
is the quadratic equation 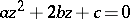 and its distinct irrational roots
and its distinct irrational roots
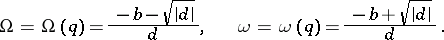 |
The form 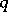 is said to be reduced if
is said to be reduced if 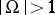 ,
, 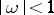 ,
, 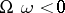 . These conditions are equivalent to the conditions
. These conditions are equivalent to the conditions
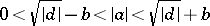 |
(and also to the conditions 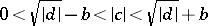 ). The number of reduced integer-valued quadratic forms of given determinant is finite. Every quadratic form is equivalent to a reduced one. There is an algorithm for reduction, using continued fractions (see [1]).
). The number of reduced integer-valued quadratic forms of given determinant is finite. Every quadratic form is equivalent to a reduced one. There is an algorithm for reduction, using continued fractions (see [1]).
For a reduced quadratic form there exists precisely one "right neighbouring" and precisely one "left neighbouring" reduced quadratic form (see [1]). By going over from a reduced quadratic form to its "neighbouring" , one obtains a doubly-infinite chain of reduced forms. This chain is periodic. A finite segment of inequivalent forms of this chain is called a period. Two reduced forms are properly equivalent if and only if one of them is in the period of the other.
The foregoing theory is valid also for forms with real coefficients 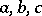 if
if 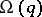 and
and 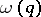 are distinct irrational roots; however, in this case a chain of reduced forms need not be periodic.
are distinct irrational roots; however, in this case a chain of reduced forms need not be periodic.
All proper automorphisms (of determinant 1) of a quadratic form with greatest common divisor 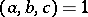 , greatest common divisor
, greatest common divisor 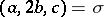 ,
, 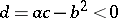 , have the form
, have the form
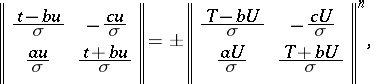 |
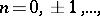 |
where 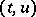 runs through all the solutions of the Pell equation
runs through all the solutions of the Pell equation 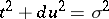 and
and 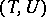 is the fundamental solution of this equation, that is, the smallest positive solution. Improper automorphisms (of determinant
is the fundamental solution of this equation, that is, the smallest positive solution. Improper automorphisms (of determinant 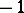 ) exist only for two-sided (or ambiguous) forms, that is, forms whose class coincides with that of its inverse (see [1]). The subgroup of proper automorphisms of a two-sided form has index 2 in the group of all automorphisms.
) exist only for two-sided (or ambiguous) forms, that is, forms whose class coincides with that of its inverse (see [1]). The subgroup of proper automorphisms of a two-sided form has index 2 in the group of all automorphisms.
Indefinite integer-valued quadratic forms of determinant 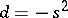 ,
, 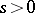 ,
, 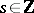 , reduce to the form
, reduce to the form 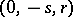 , where
, where 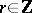 ,
, 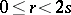 . Two quadratic forms
. Two quadratic forms 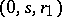 and
and 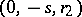 ,
, 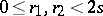 , are properly equivalent if and only if
, are properly equivalent if and only if  . All the automorphisms of such forms are
. All the automorphisms of such forms are
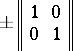 |
(see [1]).
b) Reduction of indefinite  -ary quadratic forms. Let
-ary quadratic forms. Let 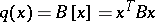 be such a form with real coefficients and
be such a form with real coefficients and 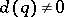 . Then there exists a change of variables (over
. Then there exists a change of variables (over 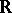 ),
), 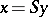 , such that
, such that
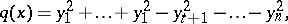 |
where 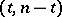 is the signature of
is the signature of 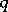 . Let
. Let
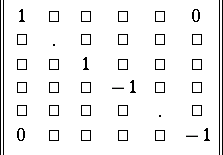 |
(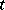 rows 1;
rows 1; 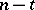 rows
rows 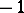 ) and
) and 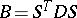 . The quadratic form
. The quadratic form 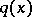 is associated with the positive-definite quadratic form
is associated with the positive-definite quadratic form
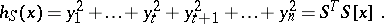 |
The form 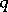 is called (Hermite) reducible if there is a transformation
is called (Hermite) reducible if there is a transformation 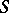 of the form
of the form 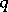 into a sum of squares such that
into a sum of squares such that 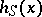 is (for example, Minkowski) reduced.
is (for example, Minkowski) reduced.
Equivalent to this definition of a reduced quadratic form is the following [13], [14]. Let 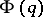 be the set of matrices
be the set of matrices 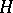 over
over 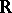 of positive
of positive  -ary quadratic forms satisfying the equation
-ary quadratic forms satisfying the equation 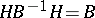 . This is a connected
. This is a connected 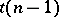 -dimensional manifold of the positivity cone
-dimensional manifold of the positivity cone 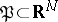 (which can be written out in explicit form). Let
(which can be written out in explicit form). Let 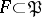 be the domain of reduction of positive-definite quadratic forms. The form
be the domain of reduction of positive-definite quadratic forms. The form 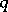 is called reducible if
is called reducible if 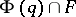 is non-empty.
is non-empty.
The number of classes of integral indefinite quadratic forms in  variables with a given determinant
variables with a given determinant 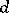 is finite (this is true also for positive-definite quadratic forms). The number of reduced forms in a given class is also finite. If two integral quadratic forms
is finite (this is true also for positive-definite quadratic forms). The number of reduced forms in a given class is also finite. If two integral quadratic forms 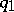 and
and 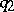 are equivalent, then there exists an integral transformation
are equivalent, then there exists an integral transformation 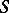 , the absolute values of the elements of which are bounded by a constant depending only on
, the absolute values of the elements of which are bounded by a constant depending only on  and
and 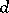 , that takes
, that takes  to
to 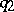 . Thus the problem of determining whether or not two indefinite integral quadratic forms are equivalent is solved in a finite number of steps.
. Thus the problem of determining whether or not two indefinite integral quadratic forms are equivalent is solved in a finite number of steps.
c) Automorphisms of indefinite quadratic forms. The problem of the description of all automorphisms of an indefinite integral quadratic form has two aspects: 1) to construct a fundamental domain of the group of automorphisms; 2) to describe the general form of the automorphisms (similar to the description of automorphisms by means of the Pell equation).
The general form of the automorphisms of a quadratic form was described by Ch. Hermite for 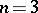 and by A. Cayley for arbitrary
and by A. Cayley for arbitrary  (see [10]).
(see [10]).
A fundamental domain has been constructed of the group of automorphisms of an indefinite integral quadratic form  in a manifold
in a manifold 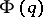 bounded by a finite number of algebraic surfaces, and its volume has been calculated [13]. For the case
bounded by a finite number of algebraic surfaces, and its volume has been calculated [13]. For the case 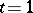 in the
in the  -dimensional space a fundamental domain has been constructed of the group of automorphisms of a quadratic form
-dimensional space a fundamental domain has been constructed of the group of automorphisms of a quadratic form 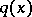 in the form of an infinite pyramid with a finite number of plane faces (see [2], [4]).
in the form of an infinite pyramid with a finite number of plane faces (see [2], [4]).
There is a reduction theory of quadratic forms in algebraic number fields (see [11]).
References
| [1] | B.A. Venkov, "Elementary number theory" , Wolters-Noordhoff (1970) (Translated from Russian) |
| [2] | B.A. Venkov, Izv. Akad. Nauk SSSR. Ser. Mat. , 1 (1937) pp. 139–170 |
| [3] | B.A. Venkov, "The reduction of positive-definite quadratic forms" Izv. Akad. Nauk SSSR. Ser. Mat. , 4 (1940) pp. 37–52 (In Russian) |
| [4] | B.A. Venkov, "On indeterminate quadratic forms with integral coefficients" Trudy Mat. Inst. Steklov. , 38 (1951) pp. 30–41 (In Russian) |
| [5a] | B.N. Delone, "The geometry of positive definite quadratic forms" Uspekhi Mat. Nauk : 3 (1937) pp. 16–62 (In Russian) |
| [5b] | B.N. Delone, "The geometry of positive definite quadratic forms" Uspekhi Mat. Nauk : 4 (1938) pp. 104–164 (In Russian) |
| [6] | B.N. Delone, R.V. Galiulin, M.I. Shtorgin, "The types of Bravais lattices" , Current problems in mathematics , 2 , Moscow (1973) pp. 119–254 (In Russian) |
| [7] | P.G. Lejeune-Dirichlet, "Vorlesungen über Zahlentheorie" , Vieweg (1894) |
| [8] | S.S. Ryshkov, "The theory of Hermite–Minkowski reduction of positive definite quadratic forms" J. Soviet Math. , 6 : 6 (1976) pp. 651–671 Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. , 33 (1973) pp. 37–64 |
| [9a] | P.P. Tammela, "Reduction theory of positive quadratic forms" J. Soviet Math. , 11 : 2 (1979) pp. 197–277 Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. , 50 (1975) pp. 6–96 |
| [9b] | P.P. Tammela, "Minkowski reduction region for positive quadratic forms in seven variables" J. Soviet Math. , 16 : 1 (1981) pp. 836–857 Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. , 67 (1977) pp. 108–143; 226 |
| [10] | P. Bachmann, "Zahlentheorie. Die Arithmetik der quadratischen Formen" , 1–2 , Teubner (1923–1925) |
| [11] | P. Humbert, "Réduction de formes quadratiques dans un corps algébrique fini" Comm. Math. Helv. , 23 (1949) pp. 50–63 |
| [12] | H. Minkowski, "Diskontinuitätsbereich für arithmetische Äquivalenz" J. Reine Angew. Math. , 129 (1905) pp. 220–274 |
| [13] | C.L. Siegel, "Einheiten quadratischer Formen" Abh. Math. Sem. Univ. Hamburg , 13 (1939) pp. 209–239 |
| [14] | C.L. Siegel, "Zur Theorie der quadratischen Formen" Nachr. Akad. Wiss. Göttingen Math.-Phys. Kl. (1972) pp. 21–46 |
| [15] | B.L. van der Waerden, "Die Reduktionstheorie der positiven quadratischen Formen" Acta Math. , 96 (1956) pp. 265–309 |
Quadratic forms, reduction of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quadratic_forms,_reduction_of&oldid=16798