Difference between revisions of "Pseudo-group structure"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | p0757101.png | ||
| + | $#A+1 = 141 n = 3 | ||
| + | $#C+1 = 141 : ~/encyclopedia/old_files/data/P075/P.0705710 Pseudo\AAhgroup structure | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | A maximal atlas | + | {{TEX|auto}} |
| + | {{TEX|done}} | ||
| + | |||
| + | ''on a manifold $ M $'' | ||
| + | |||
| + | A maximal atlas $ A $ | ||
| + | of smooth local diffeomorphisms (cf. [[Diffeomorphism|Diffeomorphism]]) from $ M $ | ||
| + | onto a fixed manifold $ V $, | ||
| + | all transition functions between them belonging to a given pseudo-group $ \Gamma $ | ||
| + | of local transformations of $ V $. | ||
| + | The pseudo-group $ \Gamma $ | ||
| + | is called the defining pseudo-group, and $ V $ | ||
| + | is called the model space. The pseudo-group structure with defining group $ \Gamma $ | ||
| + | is also called a $ \Gamma $- | ||
| + | structure. More precisely, a set $ A $ | ||
| + | of $ V $- | ||
| + | valued charts of a manifold $ M $( | ||
| + | i.e. of diffeomorphisms $ \phi : U \rightarrow V $ | ||
| + | of open subsets $ U \subset M $ | ||
| + | onto open subsets $ \phi ( U) \subset V $) | ||
| + | is called a pseudo-group structure if a) any point $ x \in M $ | ||
| + | belongs to the domain of definition of a chart $ \phi $ | ||
| + | of $ A $; | ||
| + | b) for any charts $ \phi : U \rightarrow V $ | ||
| + | and $ \psi : W \rightarrow V $ | ||
| + | from $ A $ | ||
| + | the transition function $ \psi \circ \phi ^ {-} 1 : \phi ( U \cap W ) \rightarrow \psi ( U \cap W ) $ | ||
| + | is a local transformation from the given pseudo-group $ \Gamma $; | ||
| + | and c) $ A $ | ||
| + | is a maximal set of charts satisfying condition b). | ||
===Examples of pseudo-group structures.=== | ===Examples of pseudo-group structures.=== | ||
| + | 1) A [[Pseudo-group|pseudo-group]] $ \Gamma $ | ||
| + | of transformations of a manifold $ V $ | ||
| + | gives a pseudo-group structure $ ( V , \Gamma ) $ | ||
| + | on $ V $ | ||
| + | whose charts are the local transformations of $ \Gamma $. | ||
| + | It is called the standard flat $ \Gamma $- | ||
| + | structure. | ||
| − | + | 2) Let $ V = K ^ {n} $ | |
| + | be an $ n $- | ||
| + | dimensional vector space over $ K = \mathbf R , \mathbf C $ | ||
| + | or a left module over the skew-field of quaternions $ K = \mathbf H $, | ||
| + | and let $ \Gamma $ | ||
| + | be the pseudo-group of local transformations of $ V $ | ||
| + | whose principal linear parts belong to the group $ \mathop{\rm GL} ( n , K ) $. | ||
| + | The corresponding $ \Gamma $- | ||
| + | structure on a manifold $ M $ | ||
| + | is the structure of a smooth manifold if $ K = \mathbf R $, | ||
| + | of a complex-analytic manifold if $ K = \mathbf C $ | ||
| + | and of a special quaternionic manifold if $ K = \mathbf H $. | ||
| − | + | 3) Let $ \Gamma $ | |
| + | be the pseudo-group of local transformations of a vector space $ V $ | ||
| + | preserving a given tensor $ S $. | ||
| + | Specifying a $ \Gamma $- | ||
| + | structure is equivalent to specifying an integrable (global) tensor field of type $ S $ | ||
| + | on a manifold $ M $. | ||
| + | E.g., if $ S $ | ||
| + | is a non-degenerate skew-symmetric $ 2 $- | ||
| + | form, then the $ \Gamma $- | ||
| + | structure is a [[Symplectic structure|symplectic structure]]. | ||
| − | + | 4) Let $ \Gamma $ | |
| + | be the pseudo-group of local transformations of $ \mathbf R ^ {2n+} 1 $ | ||
| + | that preserve, up to a functional multiplier, the differential $ 1 $- | ||
| + | form | ||
| − | + | $$ | |
| + | d x ^ {0} + | ||
| + | \sum _ { i= } 1 ^ { n } | ||
| + | x ^ {2i-} 1 d x ^ {2i} . | ||
| + | $$ | ||
| − | + | Then the $ \Gamma $- | |
| + | structure is a [[Contact structure|contact structure]]. | ||
| − | + | 5) Let $ V = G / H $ | |
| + | be a [[Homogeneous space|homogeneous space]] of a Lie group $ G $, | ||
| + | and let $ \Gamma $ | ||
| + | be the pseudo-group of local transformations of $ V $ | ||
| + | that can be lifted to transformations of $ G $. | ||
| + | Then the $ \Gamma $- | ||
| + | structure is called the pseudo-group structure determined by the homogeneous space $ V $. | ||
| + | Examples of such structures are the structure of a space of constant curvature (in particular, that of a locally Euclidean space), and conformally and projectively flat structures. | ||
| − | + | Let $ \Gamma $ | |
| + | be a transitive Lie pseudo-group of transformations of $ V = \mathbf R ^ {n} $ | ||
| + | of order $ l $, | ||
| + | see [[Pseudo-group|Pseudo-group]]. The $ \Gamma $- | ||
| + | structure $ A $ | ||
| + | on a manifold $ M $ | ||
| + | determines a principal subbundle $ \pi _ {k} : B ^ {k} \rightarrow M $ | ||
| + | of the co-frame bundle of arbitrary order $ k $ | ||
| + | on $ M $, | ||
| + | consisting of the $ k $- | ||
| + | jets of charts of $ A $: | ||
| − | + | $$ | |
| + | B ^ {k} = \ | ||
| + | \{ {j _ {x} ^ {k} \phi } : {\phi \in A , \phi ( x) = 0 } \} | ||
| + | ,\ \ | ||
| + | \pi _ {k} ( j _ {x} ^ {k} \phi ) = x . | ||
| + | $$ | ||
| − | + | The structure group of $ \pi _ {k} $ | |
| + | is the $ k $- | ||
| + | th order isotropy group $ G ^ {k} ( \Gamma ) $ | ||
| + | of $ \Gamma $, | ||
| + | which acts on $ B ^ {k} $ | ||
| + | by the formula | ||
| − | + | $$ | |
| + | j _ {0} ^ {k} ( a) j _ {x} ^ {k} \phi = \ | ||
| + | j _ {x} ^ {k} ( a \circ \phi ) . | ||
| + | $$ | ||
| − | + | The bundle $ \pi _ {k} $ | |
| + | is called the $ k $- | ||
| + | th structure bundle, or $ G ^ {k} ( \Gamma ) $- | ||
| + | structure, determined by the pseudo-group structure $ A $. | ||
| + | The bundle $ \pi _ {l} $, | ||
| + | with $ l $ | ||
| + | the order of $ \Gamma $, | ||
| + | in turn, uniquely determines the pseudo-group structure $ A $ | ||
| + | as the set of charts $ \phi : U \rightarrow V $ | ||
| + | for which | ||
| − | + | $$ | |
| + | j _ {x} ^ {l} ( a \circ \phi ) \in B ^ {l} \ \ | ||
| + | \textrm{ if } a \in \Gamma , a \circ \phi ( x) = 0 . | ||
| + | $$ | ||
| − | + | The geometry of $ \pi _ {k} $ | |
| + | is characterized by the presence of a canonical $ G ^ {k} ( \Gamma ) $- | ||
| + | equivariant $ 1 $- | ||
| + | form $ \theta ^ {k} : T B ^ {k} \rightarrow V + \mathfrak g ^ {k} ( V) $ | ||
| + | that is horizontal relative to the projection $ B ^ {k} \rightarrow B ^ {k-} 1 $. | ||
| + | Here $ \mathfrak g ^ {k} ( V) $ | ||
| + | is the Lie algebra of the isotropy group $ G ^ {k} ( \Gamma ) $. | ||
| + | The $ 1 $- | ||
| + | form $ \theta ^ {k} $ | ||
| + | is given by | ||
| − | + | $$ | |
| + | \left . | ||
| + | \theta _ {b ^ {k} } ^ {k} ( \dot{b} ^ {k} ) = \ | ||
| − | + | \frac{d}{dt} | |
| + | |||
| + | j _ {0} ^ {k-} 1 ( \phi _ {t} \circ \phi _ {0} ^ {-} 1 ) | ||
| + | \right | _ {t = 0 } , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | b ^ {k} = j _ {x _ {0} } ^ {k} ( \phi _ {0} ) ,\ \ | ||
| + | \dot{b} ^ {k} = | ||
| + | \frac{d}{dt} | ||
| + | j _ {x _ {t} } ^ {k} ( \phi _ {t} ) , | ||
| + | $$ | ||
| − | + | $$ | |
| + | \phi _ {t} \in A ,\ \phi _ {t} ( x _ {t} ) = 0 ,\ t \in [ 0 , \epsilon ] , | ||
| + | $$ | ||
| − | and satisfies a certain Maurer–Cartan structure equation (cf. also [[Maurer–Cartan form|Maurer–Cartan form]]). The Lie algebra of infinitesimal automorphisms of the | + | and satisfies a certain Maurer–Cartan structure equation (cf. also [[Maurer–Cartan form|Maurer–Cartan form]]). The Lie algebra of infinitesimal automorphisms of the $ \Gamma $- |
| + | structure can be characterized as the Lie algebra of projectable vector fields on $ B ^ {l} $ | ||
| + | that preserve the canonical $ 1 $- | ||
| + | form $ \theta ^ {l} $. | ||
| − | The basic problem in the theory of pseudo-group structures is the description of pseudo-group structures on manifolds with a defining pseudo-group | + | The basic problem in the theory of pseudo-group structures is the description of pseudo-group structures on manifolds with a defining pseudo-group $ \Gamma $, |
| + | up to equivalence. Two pseudo-group structures on a manifold are called equivalent if one of them can be reduced to the other by a diffeomorphism of the manifold. | ||
| − | Let | + | Let $ \Gamma $ |
| + | be a globalizing transitive pseudo-group of transformations of a simply-connected manifold $ V $. | ||
| + | Any simply-connected manifold with a $ \Gamma $- | ||
| + | structure $ A $ | ||
| + | admits a mapping $ \rho : M \rightarrow V $, | ||
| + | called a Cartan development, that locally is an isomorphism of $ \Gamma $- | ||
| + | structures. If $ A $ | ||
| + | has some completeness property, then $ \rho $ | ||
| + | is an isomorphism of $ \Gamma $- | ||
| + | structures and all $ \Gamma $- | ||
| + | structures of the type considered are forms of the standard $ \Gamma $- | ||
| + | structure $ V $, | ||
| + | i.e. are obtained from $ V $ | ||
| + | by factorization by a freely-acting discrete automorphism group $ ( V , \Gamma ) $. | ||
| + | This is the case, e.g. for (pseudo-)Riemannian structures of constant curvature and for conformally-flat structures on compact manifolds $ M ^ {n} $, | ||
| + | $ n > 2 $. | ||
| − | The theory of deformations, originally developed for complex structures, occupies an important place in the theory of pseudo-group structures. In it one studies problems of the description of non-trivial deformations of a | + | The theory of deformations, originally developed for complex structures, occupies an important place in the theory of pseudo-group structures. In it one studies problems of the description of non-trivial deformations of a $ \Gamma $- |
| + | structure $ A $, | ||
| + | i.e. a family $ A _ {t} $ | ||
| + | of $ \Gamma $- | ||
| + | structures containing the given $ \Gamma $- | ||
| + | structure and smoothly depending on a parameter $ t $, | ||
| + | modulo trivial deformations. The space of formal infinitesimal non-trivial deformations of a given $ \Gamma $- | ||
| + | structure is described by the one-dimensional cohomology space $ H ^ {1} ( M , \Theta ) $ | ||
| + | of $ M $ | ||
| + | with coefficients in the sheaf $ \Theta $ | ||
| + | of germs of infinitesimal automorphisms of $ A $. | ||
| + | The $ \Gamma $- | ||
| + | structure is rigid if this space is trivial. If the two-dimensional cohomology space is trivial, $ H ^ {2} ( H , \Theta ) = 0 $, | ||
| + | one can prove, under certain assumptions, that there exist non-trivial deformations of the $ \Gamma $- | ||
| + | structure, corresponding to given infinitesimal deformations from $ H ^ {1} ( M , \Theta ) $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Cartan, "La géométrie des éspaces Riemanniennes" , ''Mém. Sci. Math.'' , '''9''' , Gauthier-Villars (1925)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V. Guillemin, S. Sternberg, "Deformation theory of pseudogroup structures" , ''Mem. Amer. Math. Soc.'' , '''64''' , Amer. Math. Soc. (1966)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.S. Pollack, "The integrability of pseudogroup structures" ''J. Diff. Geom.'' , '''9''' : 3 (1974) pp. 355–390</TD></TR><TR><TD valign="top">[4a]</TD> <TD valign="top"> P.A. Griffiths, "Deformations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075710/p075710145.png" />-structures. Part A: General theory of deformations" ''Math. Ann.'' , '''155''' : 4 (1964) pp. 292–315</TD></TR><TR><TD valign="top">[4b]</TD> <TD valign="top"> P.A. Griffiths, "Deformations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075710/p075710146.png" />-structures. Part B: Deformations of geometric <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075710/p075710147.png" />-structures" ''Math. Ann.'' , '''158''' : 5 (1965) pp. 326–351</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.F. Pommaret, "Théorie des déformations des structures" ''Ann. Inst. H. Poincaré Nouvelle Sér.'' , '''18''' (1973) pp. 285–352 (English abstract)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> L. Berard Bergery, J.-P. Bourgignon, J. Lafontaine, "Déformations localement triviales des variétés Riemanniennes" , ''Differential geometry'' , ''Proc. Symp. Pure Math.'' , '''27''' , Amer. Math. Soc. (1975) pp. 3–32</TD></TR><TR><TD valign="top">[7a]</TD> <TD valign="top"> D.C. Spencer, "Deformation of structures on manifolds defined by transitive, continuous pseudogroups I. Infinitesimal deformations of structure" ''Ann. of Math.'' , '''76''' : 2 (1962) pp. 306–398</TD></TR><TR><TD valign="top">[7b]</TD> <TD valign="top"> D.C. Spencer, "Deformation of structures on manifolds defined by transitive, continuous pseudogroups II. Deformations of structure" ''Ann. of Math.'' , '''76''' : 3 (1962) pp. 399–445</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Cartan, "La géométrie des éspaces Riemanniennes" , ''Mém. Sci. Math.'' , '''9''' , Gauthier-Villars (1925)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V. Guillemin, S. Sternberg, "Deformation theory of pseudogroup structures" , ''Mem. Amer. Math. Soc.'' , '''64''' , Amer. Math. Soc. (1966)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.S. Pollack, "The integrability of pseudogroup structures" ''J. Diff. Geom.'' , '''9''' : 3 (1974) pp. 355–390</TD></TR><TR><TD valign="top">[4a]</TD> <TD valign="top"> P.A. Griffiths, "Deformations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075710/p075710145.png" />-structures. Part A: General theory of deformations" ''Math. Ann.'' , '''155''' : 4 (1964) pp. 292–315</TD></TR><TR><TD valign="top">[4b]</TD> <TD valign="top"> P.A. Griffiths, "Deformations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075710/p075710146.png" />-structures. Part B: Deformations of geometric <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p075/p075710/p075710147.png" />-structures" ''Math. Ann.'' , '''158''' : 5 (1965) pp. 326–351</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.F. Pommaret, "Théorie des déformations des structures" ''Ann. Inst. H. Poincaré Nouvelle Sér.'' , '''18''' (1973) pp. 285–352 (English abstract)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> L. Berard Bergery, J.-P. Bourgignon, J. Lafontaine, "Déformations localement triviales des variétés Riemanniennes" , ''Differential geometry'' , ''Proc. Symp. Pure Math.'' , '''27''' , Amer. Math. Soc. (1975) pp. 3–32</TD></TR><TR><TD valign="top">[7a]</TD> <TD valign="top"> D.C. Spencer, "Deformation of structures on manifolds defined by transitive, continuous pseudogroups I. Infinitesimal deformations of structure" ''Ann. of Math.'' , '''76''' : 2 (1962) pp. 306–398</TD></TR><TR><TD valign="top">[7b]</TD> <TD valign="top"> D.C. Spencer, "Deformation of structures on manifolds defined by transitive, continuous pseudogroups II. Deformations of structure" ''Ann. of Math.'' , '''76''' : 3 (1962) pp. 399–445</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | For the topic of classifying spaces for | + | For the topic of classifying spaces for $ \Gamma $- |
| + | structures cf. [[#References|[a2]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , '''1''' , Interscience (1963) pp. Chapt. 1</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Haefliger, "Homotopy and integrability" J.N. Mordeson (ed.) et al. (ed.) , ''Structure of arbitrary purely inseparable extension fields'' , ''Lect. notes in math.'' , '''173''' , Springer (1971) pp. 133–163</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.F. Pommaret, "Systems of partial differential equations and Lie pseudogroups" , Gordon & Breach (1978)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , ''Deformation theory of algebras and structures and applications'' , Kluwer (1988)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , '''1''' , Interscience (1963) pp. Chapt. 1</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Haefliger, "Homotopy and integrability" J.N. Mordeson (ed.) et al. (ed.) , ''Structure of arbitrary purely inseparable extension fields'' , ''Lect. notes in math.'' , '''173''' , Springer (1971) pp. 133–163</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.F. Pommaret, "Systems of partial differential equations and Lie pseudogroups" , Gordon & Breach (1978)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , ''Deformation theory of algebras and structures and applications'' , Kluwer (1988)</TD></TR></table> | ||
Revision as of 08:08, 6 June 2020
on a manifold $ M $
A maximal atlas $ A $ of smooth local diffeomorphisms (cf. Diffeomorphism) from $ M $ onto a fixed manifold $ V $, all transition functions between them belonging to a given pseudo-group $ \Gamma $ of local transformations of $ V $. The pseudo-group $ \Gamma $ is called the defining pseudo-group, and $ V $ is called the model space. The pseudo-group structure with defining group $ \Gamma $ is also called a $ \Gamma $- structure. More precisely, a set $ A $ of $ V $- valued charts of a manifold $ M $( i.e. of diffeomorphisms $ \phi : U \rightarrow V $ of open subsets $ U \subset M $ onto open subsets $ \phi ( U) \subset V $) is called a pseudo-group structure if a) any point $ x \in M $ belongs to the domain of definition of a chart $ \phi $ of $ A $; b) for any charts $ \phi : U \rightarrow V $ and $ \psi : W \rightarrow V $ from $ A $ the transition function $ \psi \circ \phi ^ {-} 1 : \phi ( U \cap W ) \rightarrow \psi ( U \cap W ) $ is a local transformation from the given pseudo-group $ \Gamma $; and c) $ A $ is a maximal set of charts satisfying condition b).
Examples of pseudo-group structures.
1) A pseudo-group $ \Gamma $ of transformations of a manifold $ V $ gives a pseudo-group structure $ ( V , \Gamma ) $ on $ V $ whose charts are the local transformations of $ \Gamma $. It is called the standard flat $ \Gamma $- structure.
2) Let $ V = K ^ {n} $ be an $ n $- dimensional vector space over $ K = \mathbf R , \mathbf C $ or a left module over the skew-field of quaternions $ K = \mathbf H $, and let $ \Gamma $ be the pseudo-group of local transformations of $ V $ whose principal linear parts belong to the group $ \mathop{\rm GL} ( n , K ) $. The corresponding $ \Gamma $- structure on a manifold $ M $ is the structure of a smooth manifold if $ K = \mathbf R $, of a complex-analytic manifold if $ K = \mathbf C $ and of a special quaternionic manifold if $ K = \mathbf H $.
3) Let $ \Gamma $ be the pseudo-group of local transformations of a vector space $ V $ preserving a given tensor $ S $. Specifying a $ \Gamma $- structure is equivalent to specifying an integrable (global) tensor field of type $ S $ on a manifold $ M $. E.g., if $ S $ is a non-degenerate skew-symmetric $ 2 $- form, then the $ \Gamma $- structure is a symplectic structure.
4) Let $ \Gamma $ be the pseudo-group of local transformations of $ \mathbf R ^ {2n+} 1 $ that preserve, up to a functional multiplier, the differential $ 1 $- form
$$ d x ^ {0} + \sum _ { i= } 1 ^ { n } x ^ {2i-} 1 d x ^ {2i} . $$
Then the $ \Gamma $- structure is a contact structure.
5) Let $ V = G / H $ be a homogeneous space of a Lie group $ G $, and let $ \Gamma $ be the pseudo-group of local transformations of $ V $ that can be lifted to transformations of $ G $. Then the $ \Gamma $- structure is called the pseudo-group structure determined by the homogeneous space $ V $. Examples of such structures are the structure of a space of constant curvature (in particular, that of a locally Euclidean space), and conformally and projectively flat structures.
Let $ \Gamma $ be a transitive Lie pseudo-group of transformations of $ V = \mathbf R ^ {n} $ of order $ l $, see Pseudo-group. The $ \Gamma $- structure $ A $ on a manifold $ M $ determines a principal subbundle $ \pi _ {k} : B ^ {k} \rightarrow M $ of the co-frame bundle of arbitrary order $ k $ on $ M $, consisting of the $ k $- jets of charts of $ A $:
$$ B ^ {k} = \ \{ {j _ {x} ^ {k} \phi } : {\phi \in A , \phi ( x) = 0 } \} ,\ \ \pi _ {k} ( j _ {x} ^ {k} \phi ) = x . $$
The structure group of $ \pi _ {k} $ is the $ k $- th order isotropy group $ G ^ {k} ( \Gamma ) $ of $ \Gamma $, which acts on $ B ^ {k} $ by the formula
$$ j _ {0} ^ {k} ( a) j _ {x} ^ {k} \phi = \ j _ {x} ^ {k} ( a \circ \phi ) . $$
The bundle $ \pi _ {k} $ is called the $ k $- th structure bundle, or $ G ^ {k} ( \Gamma ) $- structure, determined by the pseudo-group structure $ A $. The bundle $ \pi _ {l} $, with $ l $ the order of $ \Gamma $, in turn, uniquely determines the pseudo-group structure $ A $ as the set of charts $ \phi : U \rightarrow V $ for which
$$ j _ {x} ^ {l} ( a \circ \phi ) \in B ^ {l} \ \ \textrm{ if } a \in \Gamma , a \circ \phi ( x) = 0 . $$
The geometry of $ \pi _ {k} $ is characterized by the presence of a canonical $ G ^ {k} ( \Gamma ) $- equivariant $ 1 $- form $ \theta ^ {k} : T B ^ {k} \rightarrow V + \mathfrak g ^ {k} ( V) $ that is horizontal relative to the projection $ B ^ {k} \rightarrow B ^ {k-} 1 $. Here $ \mathfrak g ^ {k} ( V) $ is the Lie algebra of the isotropy group $ G ^ {k} ( \Gamma ) $. The $ 1 $- form $ \theta ^ {k} $ is given by
$$ \left . \theta _ {b ^ {k} } ^ {k} ( \dot{b} ^ {k} ) = \ \frac{d}{dt} j _ {0} ^ {k-} 1 ( \phi _ {t} \circ \phi _ {0} ^ {-} 1 ) \right | _ {t = 0 } , $$
where
$$ b ^ {k} = j _ {x _ {0} } ^ {k} ( \phi _ {0} ) ,\ \ \dot{b} ^ {k} = \frac{d}{dt} j _ {x _ {t} } ^ {k} ( \phi _ {t} ) , $$
$$ \phi _ {t} \in A ,\ \phi _ {t} ( x _ {t} ) = 0 ,\ t \in [ 0 , \epsilon ] , $$
and satisfies a certain Maurer–Cartan structure equation (cf. also Maurer–Cartan form). The Lie algebra of infinitesimal automorphisms of the $ \Gamma $- structure can be characterized as the Lie algebra of projectable vector fields on $ B ^ {l} $ that preserve the canonical $ 1 $- form $ \theta ^ {l} $.
The basic problem in the theory of pseudo-group structures is the description of pseudo-group structures on manifolds with a defining pseudo-group $ \Gamma $, up to equivalence. Two pseudo-group structures on a manifold are called equivalent if one of them can be reduced to the other by a diffeomorphism of the manifold.
Let $ \Gamma $ be a globalizing transitive pseudo-group of transformations of a simply-connected manifold $ V $. Any simply-connected manifold with a $ \Gamma $- structure $ A $ admits a mapping $ \rho : M \rightarrow V $, called a Cartan development, that locally is an isomorphism of $ \Gamma $- structures. If $ A $ has some completeness property, then $ \rho $ is an isomorphism of $ \Gamma $- structures and all $ \Gamma $- structures of the type considered are forms of the standard $ \Gamma $- structure $ V $, i.e. are obtained from $ V $ by factorization by a freely-acting discrete automorphism group $ ( V , \Gamma ) $. This is the case, e.g. for (pseudo-)Riemannian structures of constant curvature and for conformally-flat structures on compact manifolds $ M ^ {n} $, $ n > 2 $.
The theory of deformations, originally developed for complex structures, occupies an important place in the theory of pseudo-group structures. In it one studies problems of the description of non-trivial deformations of a $ \Gamma $- structure $ A $, i.e. a family $ A _ {t} $ of $ \Gamma $- structures containing the given $ \Gamma $- structure and smoothly depending on a parameter $ t $, modulo trivial deformations. The space of formal infinitesimal non-trivial deformations of a given $ \Gamma $- structure is described by the one-dimensional cohomology space $ H ^ {1} ( M , \Theta ) $ of $ M $ with coefficients in the sheaf $ \Theta $ of germs of infinitesimal automorphisms of $ A $. The $ \Gamma $- structure is rigid if this space is trivial. If the two-dimensional cohomology space is trivial, $ H ^ {2} ( H , \Theta ) = 0 $, one can prove, under certain assumptions, that there exist non-trivial deformations of the $ \Gamma $- structure, corresponding to given infinitesimal deformations from $ H ^ {1} ( M , \Theta ) $.
References
| [1] | E. Cartan, "La géométrie des éspaces Riemanniennes" , Mém. Sci. Math. , 9 , Gauthier-Villars (1925) |
| [2] | V. Guillemin, S. Sternberg, "Deformation theory of pseudogroup structures" , Mem. Amer. Math. Soc. , 64 , Amer. Math. Soc. (1966) |
| [3] | A.S. Pollack, "The integrability of pseudogroup structures" J. Diff. Geom. , 9 : 3 (1974) pp. 355–390 |
| [4a] | P.A. Griffiths, "Deformations of 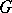 -structures. Part A: General theory of deformations" Math. Ann. , 155 : 4 (1964) pp. 292–315 -structures. Part A: General theory of deformations" Math. Ann. , 155 : 4 (1964) pp. 292–315 |
| [4b] | P.A. Griffiths, "Deformations of 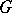 -structures. Part B: Deformations of geometric -structures. Part B: Deformations of geometric 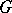 -structures" Math. Ann. , 158 : 5 (1965) pp. 326–351 -structures" Math. Ann. , 158 : 5 (1965) pp. 326–351 |
| [5] | J.F. Pommaret, "Théorie des déformations des structures" Ann. Inst. H. Poincaré Nouvelle Sér. , 18 (1973) pp. 285–352 (English abstract) |
| [6] | L. Berard Bergery, J.-P. Bourgignon, J. Lafontaine, "Déformations localement triviales des variétés Riemanniennes" , Differential geometry , Proc. Symp. Pure Math. , 27 , Amer. Math. Soc. (1975) pp. 3–32 |
| [7a] | D.C. Spencer, "Deformation of structures on manifolds defined by transitive, continuous pseudogroups I. Infinitesimal deformations of structure" Ann. of Math. , 76 : 2 (1962) pp. 306–398 |
| [7b] | D.C. Spencer, "Deformation of structures on manifolds defined by transitive, continuous pseudogroups II. Deformations of structure" Ann. of Math. , 76 : 3 (1962) pp. 399–445 |
Comments
For the topic of classifying spaces for $ \Gamma $- structures cf. [a2].
References
| [a1] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1 , Interscience (1963) pp. Chapt. 1 |
| [a2] | A. Haefliger, "Homotopy and integrability" J.N. Mordeson (ed.) et al. (ed.) , Structure of arbitrary purely inseparable extension fields , Lect. notes in math. , 173 , Springer (1971) pp. 133–163 |
| [a3] | J.F. Pommaret, "Systems of partial differential equations and Lie pseudogroups" , Gordon & Breach (1978) |
| [a4] | M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , Deformation theory of algebras and structures and applications , Kluwer (1988) |
Pseudo-group structure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pseudo-group_structure&oldid=48347