Primitive ideal
From Encyclopedia of Mathematics
right primitive ideal
A two-sided ideal  of an associative ring
of an associative ring  (cf. Associative rings and algebras) such that the quotient ring
(cf. Associative rings and algebras) such that the quotient ring  is a (right) primitive ring. Analogously, by using left primitive rings one can define left primitive ideals. The set
is a (right) primitive ring. Analogously, by using left primitive rings one can define left primitive ideals. The set  of all primitive ideals of a ring, endowed with some topology, is useful in the study of various classes of rings. Usually
of all primitive ideals of a ring, endowed with some topology, is useful in the study of various classes of rings. Usually  is topologized using the following closure relation:
is topologized using the following closure relation:
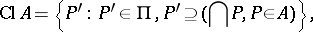 |
where  is a subset in
is a subset in  . The set of all primitive ideals of a ring endowed with this topology is called the structure space of this ring.
. The set of all primitive ideals of a ring endowed with this topology is called the structure space of this ring.
References
| [1] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) |
How to Cite This Entry:
Primitive ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Primitive_ideal&oldid=16446
Primitive ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Primitive_ideal&oldid=16446
This article was adapted from an original article by K.A. Zhevlakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article