Difference between revisions of "Power series"
Ulf Rehmann (talk | contribs) m (tex done) |
|||
| Line 1: | Line 1: | ||
| − | {{TEX| | + | {{TEX|done}} |
| − | Power series in one complex variable | + | Power series in one complex variable $ z $. |
A series (representing a function) of the form | A series (representing a function) of the form | ||
| − | + | $$ \tag{1 } | |
| + | s(z) \ = \ \sum _ { k=0 } ^ \infty b _ {k} (z-a) ^ {k} , | ||
| + | $$ | ||
| − | where | + | where $ a $ |
| + | is the centre, $ b _ {k} $ | ||
| + | are the coefficients and $ b _ {k} (z-a) ^ {k} $ | ||
| + | are the terms of the series. There exists a number $ r $, | ||
| + | $ 0 \leq r \leq \infty $, | ||
| + | called the radius of convergence of the power series (1) and determined by the Cauchy–Hadamard formula | ||
| − | + | $$ \tag{2 } | |
| + | r \ = \ | ||
| + | \frac{1}{\lim\limits _ {k \rightarrow \infty } \ \sup \ | b _ {k} | ^ {1/k} } | ||
| + | , | ||
| + | $$ | ||
| − | such that if < | + | such that if $ | z-a | < r $ |
| + | the series (1) converges absolutely, while if $ | z-a | > r $, | ||
| + | it diverges (the Cauchy–Hadamard theorem). Accordingly, the disc $ D = \{ {z \in \mathbf C } : {| z-a | < r } \} $ | ||
| + | in the complex $ z $- | ||
| + | plane $ \mathbf C $ | ||
| + | is called the disc of convergence of the power series (Fig. a). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p074240a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p074240a.gif" /> | ||
| Line 17: | Line 33: | ||
Figure: p074240a | Figure: p074240a | ||
| − | When | + | When $ r=0 $, |
| + | the disc of convergence degenerates to the single point $ z=a $, | ||
| + | for example for the power series $ \sum _ {k=0} ^ \infty k!(z-a) ^ {k} $( | ||
| + | this case is not of interest, and it is assumed from now on that $ r> 0 $). | ||
| + | When $ r = \infty $, | ||
| + | the disc of convergence coincides with the entire plane $ \mathbf C $, | ||
| + | for example for the power series $ \sum _ {k=0} ^ \infty (z-a) ^ {k} /k! $. | ||
| + | The set of convergence, i.e. the set of all points of convergence of the series (1), when $ 0 < r < \infty $, | ||
| + | consists of the points of the disc of convergence $ D $ | ||
| + | plus all, some or none of the points of the circle of convergence $ S = \{ {z \in \mathbf C } : {| z-a | = r } \} $. | ||
| + | The disc of convergence in this case is the interior of the set of points of absolute convergence of the power series. | ||
| − | Within | + | Within $ D $, |
| + | i.e. on any compact set $ K \subset D $, | ||
| + | the power series (1) converges absolutely and uniformly. Thus, the sum of the series, $ s(z) $, | ||
| + | is defined, and is a regular [[Analytic function|analytic function]] at least inside $ D $. | ||
| + | It has at least one singular point on $ S $ | ||
| + | to which the sum $ s(z) $ | ||
| + | cannot be analytically continued. There exist power series with exactly one singular point on $ S $; | ||
| + | there also exist power series for which the entire circle $ S $ | ||
| + | consists of singular points. | ||
| − | When | + | When $ r = \infty $, |
| + | the series (1) either terminates, i.e. it is a polynomial, | ||
| − | + | $$ | |
| + | s(z) \ = \ \sum _ { k=0 } ^ { m } b _ {k} (z-a) ^ {k} , | ||
| + | $$ | ||
| − | or its sum is an entire transcendental function, which is regular in the entire place | + | or its sum is an entire transcendental function, which is regular in the entire place $ \mathbf C $ |
| + | and which possesses an [[Essential singular point|essential singular point]] at infinity. | ||
| − | Conversely, the very concept of analyticity of a function | + | Conversely, the very concept of analyticity of a function $ f(z) $ |
| + | at a point $ a $ | ||
| + | is based on the fact that in a neighbourhood of $ a $, | ||
| + | $ f(z) $ | ||
| + | can be expanded into a power series | ||
| − | + | $$ | |
| + | f(z) \ = \ \sum _ { k=0 } ^ \infty b _ {k} (z-a) ^ {k} , | ||
| + | $$ | ||
| − | which is the [[Taylor series|Taylor series]] for | + | which is the [[Taylor series|Taylor series]] for $ f(z) $, |
| + | i.e. its coefficients are defined by the formulas | ||
| − | + | $$ | |
| + | b _ {k} \ = \ | ||
| + | \frac{f ^ {\ (k) } (a) }{k!} | ||
| + | . | ||
| + | $$ | ||
| − | Consequently, the uniqueness property of a power series is important: If the sum | + | Consequently, the uniqueness property of a power series is important: If the sum $ s(z) $ |
| + | of the series (1) vanishes on an infinite set $ E \subset D $ | ||
| + | with a limit point inside $ D $, | ||
| + | then $ s(z) \equiv 0 $, | ||
| + | and all $ b _ {k} = 0 $, | ||
| + | $ k = 0,\ 1 ,\dots $. | ||
| + | In particular, if $ s(z) = 0 $ | ||
| + | in a neighbourhood of a certain point $ z _ {0} \in D $, | ||
| + | then $ s(z) \equiv 0 $ | ||
| + | and all $ b _ {k} = 0 $. | ||
Thus, every power series is the Taylor series for its own sum. | Thus, every power series is the Taylor series for its own sum. | ||
| Line 41: | Line 99: | ||
Let there be another power series apart from (1): | Let there be another power series apart from (1): | ||
| − | + | $$ \tag{3 } | |
| + | \sigma (z) \ = \ \sum _ { k=0 } ^ \infty c _ {k} (z-a) ^ {k} | ||
| + | $$ | ||
| − | with the same centre | + | with the same centre $ a $ |
| + | and with radius of convergence $ r _ {1} > 0 $. | ||
| + | Then, at least inside the disc $ \Delta = \{ {z \in \mathbf C } : {| z-a | < \rho } \} $, | ||
| + | where $ \rho = \mathop{\rm min} \{ r,\ r _ {1} \} $, | ||
| + | the addition, subtraction and multiplication of the series (1) and (3) according to the following formulas hold: | ||
| − | + | $$ \tag{4 } | |
| + | \left . | ||
| + | \begin{array}{c} | ||
| − | + | s(z) \pm \sigma (z) \ = \ \sum _ { k=0 } ^ \infty (b _ {k} \pm c _ {k} )(z-a) ^ {k} , | |
| + | \\ | ||
| − | + | s(z) \sigma (z) \ = \ | |
| + | \sum _ { k=0 } ^ \infty \left ( \sum _ { n=0 } ^ { k } b _ {n} c _ {k-n} \right ) (z-a) ^ {k} | ||
| + | \end{array} | ||
| + | \right \} . | ||
| + | $$ | ||
| − | + | The laws of commutativity, associativity and distributivity hold, whereby subtraction is the inverse operation of addition. Thus, the set of power series with positive radii of convergence and a fixed centre is a [[Ring|ring]] over the field $ \mathbf C $. | |
| + | If $ c _ {0} \neq 0 $, | ||
| + | then division of power series is possible: | ||
| − | + | $$ \tag{5 } | |
| − | + | \frac{s(z)}{\sigma (z) } | |
| + | \ = \ | ||
| + | \sum _ { k=0 } ^ \infty d _ {k} (z-a) ^ {k} , | ||
| + | $$ | ||
| − | + | where the coefficients $ d _ {k} $ | |
| + | are uniquely defined from the infinite system of equations | ||
| − | + | $$ | |
| + | \sum _ { n=0 } ^ { k } c _ {n} d _ {k-n} \ = \ a _ {k} ,\ \ | ||
| + | k = 0,\ 1 ,\dots. | ||
| + | $$ | ||
| − | + | When $ c _ {0} \neq 0 $, | |
| + | $ r > 0 $ | ||
| + | and $ r _ {1} > 0 $, | ||
| + | the radius of convergence of (5) is also positive. | ||
| − | + | For the sake of simplicity, let $ a = \sigma (0) = c _ {0} = 0 $ | |
| + | in (1) and (3); the composite function $ s( \sigma (z)) $ | ||
| + | will then be regular in a neighbourhood of the coordinate origin, and the process of expanding it into a power series is called substitution of a series in a series: | ||
| + | |||
| + | $$ \tag{6 } | ||
| + | s( \sigma (z)) \ = \ | ||
| + | \sum _ { n=0 } ^ \infty b _ {n} \left ( \sum _ { k=0 } ^ \infty c _ {k} z ^ {k} \right ) ^ {n} \ = \ \sum _ { m=0 } ^ \infty g _ {m} z ^ {m} . | ||
| + | $$ | ||
| + | |||
| + | The coefficient $ g _ {m} $ | ||
| + | in (6) is obtained as the sum of the coefficients with the same index in the expansion of each of the functions $ b _ {n} ( \sigma (z)) ^ {n} $, | ||
| + | while the latter expansions are obtained by $ n $- | ||
| + | fold multiplication of the series for $ \sigma (z) $ | ||
| + | by itself. The series (6) automatically converges when $ | z | < \rho $, | ||
| + | where $ \rho $ | ||
| + | is such that $ | \sigma (z) | < r $. | ||
| + | Let $ a = \sigma (0) = c _ {0} = 0 $ | ||
| + | again, and, moreover, let $ c _ {1} = \sigma ^ \prime (0) \neq 0 $, | ||
| + | $ w = \sigma (z) $. | ||
| + | The problem of constructing a series for the inverse function $ z = \phi (w) $, | ||
| + | which under the given conditions is regular in a neighbourhood of the origin, is called inversion of the series (3). Its solution is the Lagrange series: | ||
| + | |||
| + | $$ | ||
| + | z \ = \ \phi (w) \ = \ | ||
| + | \sum _ { n=1 } ^ \infty | ||
| + | \frac{1}{n!} | ||
| + | \left ( | ||
| + | \frac \zeta {\sigma ( \zeta ) } | ||
| + | \right ) _ {\zeta | ||
| + | =0 } ^ {(n)} w ^ {n} | ||
| + | $$ | ||
(for a more general inversion problem see [[Bürmann–Lagrange series|Bürmann–Lagrange series]]). | (for a more general inversion problem see [[Bürmann–Lagrange series|Bürmann–Lagrange series]]). | ||
| − | If the power series (1) converges at a point | + | If the power series (1) converges at a point $ z _ {0} \neq a $, |
| + | then it converges absolutely for all $ z $ | ||
| + | for which $ | z-a | < | z _ {0} -a | $; | ||
| + | this is the essence of Abel's first theorem. This theorem also makes it possible to establish the form of the domain of convergence of the series. Abel's second theorem provides a more detailed result: If the series (1) converges at the point $ z _ {0} = a + re ^ {i \theta _ {0} } $ | ||
| + | on the circle of convergence $ S $, | ||
| + | then | ||
| − | + | $$ | |
| + | \lim\limits _ {\rho \rightarrow r } \ s(a+ \rho e ^ {i \theta _ {0} } ) \ = \ s(z _ {0} ), | ||
| + | $$ | ||
| − | i.e. the sum of the series, | + | i.e. the sum of the series, $ s(z) $, |
| + | at the point $ z _ {0} \in S $ | ||
| + | has radial boundary value $ s(z _ {0} ) $ | ||
| + | and, consequently, is continuous along the radius $ z = a + \rho ^ {i \theta _ {0} } $, | ||
| + | $ 0 \leq \rho \leq r $; | ||
| + | moreover, $ s(z) $ | ||
| + | also has non-tangential boundary value $ s(z _ {0} ) $( | ||
| + | cf. [[Angular boundary value|Angular boundary value]]). This theorem, dating back to 1827, can be seen as the first major result in the research into the boundary properties of power series. Inversion of Abel's second theorem without extra restrictions on the coefficients of the power series is impossible. However, if one assumes, for example, that $ b _ {k} = o(1/k) $, | ||
| + | and if $ \lim\limits _ {\rho \rightarrow r } \ s(a+ \rho e ^ {i \theta _ {0} } ) = s _ {0} $ | ||
| + | exists, then $ \sum _ {k=0} ^ \infty b _ {k} (z _ {0} -a) ^ {k} $ | ||
| + | converges to $ s _ {0} $. | ||
| + | This type of partial inversions of Abel's second theorem are called [[Tauberian theorems|Tauberian theorems]]. | ||
For other results relating to the boundary properties of power series and particularly to the location of singular points of power series, see [[Hadamard theorem|Hadamard theorem]]; [[Analytic continuation|Analytic continuation]]; [[Boundary properties of analytic functions|Boundary properties of analytic functions]]; [[Fatou theorem|Fatou theorem]] (see also –). | For other results relating to the boundary properties of power series and particularly to the location of singular points of power series, see [[Hadamard theorem|Hadamard theorem]]; [[Analytic continuation|Analytic continuation]]; [[Boundary properties of analytic functions|Boundary properties of analytic functions]]; [[Fatou theorem|Fatou theorem]] (see also –). | ||
| − | Power series in several complex variables | + | Power series in several complex variables $ z = (z _ {1} \dots z _ {n} ) $, |
| + | $ n > 1 $, | ||
| + | or multiple power series, are series (representing functions) of the form | ||
| − | + | $$ \tag{7 } | |
| + | s(z) \ = \ \sum _ {\mid k \vDash0 } ^ \infty b _ {k} (z-a) ^ {k\ } = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| + | \sum _ {k _ {1} = 0 } ^ \infty \dots \sum _ {k _ {n} =0 } ^ \infty b _ {k _ {1} \dots k _ {n} } (z _ {1} - a _ {1} ) ^ {k _ {1} } \dots (z _ {n} - a _ {n} ) ^ {k _ {n} } , | ||
| + | $$ | ||
| − | where | + | where $ b _ {k} = b _ {k _ {1} \dots k _ {n} } $, |
| + | $ (z-a) ^ {k} = (z _ {1} - a _ {1} ) ^ {k _ {1} } \dots (z _ {n} - a _ {n} ) ^ {k _ {n} } $, | ||
| + | $ | k | = k _ {1} + \dots + k _ {n} $, | ||
| + | and $ a = (a _ {1} \dots a _ {n} ) $, | ||
| + | the centre of the series, is a point of the complex space $ \mathbf C ^ {n} $. | ||
| + | The interior of the set of points of absolute convergence is called the domain of convergence $ D $ | ||
| + | of the power series (7), but when $ n > 1 $, | ||
| + | it does not have such a simple form as when $ n=1 $. | ||
| + | A domain $ D $ | ||
| + | of $ \mathbf C ^ {n} $ | ||
| + | is the domain of convergence of a certain power series (7) if and only if $ D $ | ||
| + | is a logarithmically-convex complete [[Reinhardt domain|Reinhardt domain]] of $ \mathbf C ^ {n} $. | ||
| + | If a certain point $ z ^ {0} \in D $, | ||
| + | then the closure $ \overline{U}\; (a,\ r) $ | ||
| + | of the polydisc $ U(a,\ r) = \{ {z \in \mathbf C ^ {n} } : {| z _ {v} - a _ {v} | < r _ {v} ,\ v = 1 \dots n } \} $, | ||
| + | where $ r _ {v} = | z _ {v} ^ {0} - a _ {v} | $, | ||
| + | $ r = (r _ {1} \dots r _ {n} ) $, | ||
| + | also belongs to $ D $, | ||
| + | and the series (7) converges absolutely and uniformly in $ \overline{U}\; (a,\ r) $( | ||
| + | the analogue of Abel's first theorem). The polydisc $ U(a,\ r) $, | ||
| + | $ r=(r _ {1} \dots r _ {n} ) $, | ||
| + | is called the polydisc of convergence of the series (7), if $ U(a,\ r) \subset D $ | ||
| + | and if in any larger polydisc $ \{ {z \in \mathbf C ^ {n} } : {| z _ {v} - a _ {v} | < r _ {v} ^ \prime } \} $, | ||
| + | where $ r _ {v} ^ \prime \geq r _ {v} $, | ||
| + | $ v = 1 \dots n $, | ||
| + | and at least one inequality is strict, there are points at which the series (7) diverges. The radii $ r _ {v} $ | ||
| + | of the polydisc of convergence are called conjugate radii of convergence, and satisfy a relation analogous to the Cauchy–Hadamard formula: | ||
| − | + | $$ | |
| + | \lim\limits _ {| k | \rightarrow \infty } \ \sup \ | ||
| + | (| b _ {k} | r ^ {k} ) ^ {1/ | k | } \ = \ 1, | ||
| + | $$ | ||
| − | where | + | where $ | b _ {k} | = | b _ {k _ {1} } \dots b _ {k _ {n} } | $, |
| + | $ r ^ {k} = r _ {1} ^ {k _ {1} } \dots r _ {n} ^ {k _ {n} } $. | ||
| + | The domain of convergence $ D $ | ||
| + | is exhausted by polydiscs of convergence. For example, for the series $ \sum _ {k=0} ^ \infty (z _ {1} z _ {2} ) ^ {k} $ | ||
| + | the polydiscs of convergence take the form | ||
| − | + | $$ | |
| + | U \left ( 0,\ r _ {1} ,\ | ||
| + | \frac{1}{r _ {1} } | ||
| + | \right ) \ = \ | ||
| + | \left \{ {z = (z _ {1} ,\ z _ {2} ) \in \mathbf C ^ {2} } : {| z _ {1} | < r _ {1} ,\ | z _ {2} | < | ||
| + | \frac{1}{r _ {1} } | ||
| + | } \right \} | ||
| + | , | ||
| + | $$ | ||
| − | while the domain of convergence is | + | while the domain of convergence is $ D = \{ {z \in \mathbf C ^ {2} } : {| z _ {1} | \cdot | z _ {2} | < 1 } \} $( |
| + | in Fig. bit is represented in the quadrant of absolute values). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p074240b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/p074240b.gif" /> | ||
| Line 95: | Line 275: | ||
Figure: p074240b | Figure: p074240b | ||
| − | The uniqueness property of power series is preserved in the sense that if | + | The uniqueness property of power series is preserved in the sense that if $ s(z) = 0 $ |
| + | in a neighbourhood of the point $ z ^ {0} $ | ||
| + | in $ \mathbf C ^ {n} $( | ||
| + | it is sufficient even in $ \mathbf R ^ {n} $, | ||
| + | i.e. on a set $ \{ {z = x + iy \in \mathbf C ^ {n} } : {| x - \mathop{\rm Re} \ a | < r,\ y = \mathop{\rm Im} \ a } \} $), | ||
| + | then $ s(z) \equiv 0 $ | ||
| + | and all $ b _ {k} = 0 $. | ||
| − | Operations with multiple power series are carried out, broadly speaking, according to the same rules as when | + | Operations with multiple power series are carried out, broadly speaking, according to the same rules as when $ n=1 $. |
| + | For other properties of multiple power series, see, for example, , . | ||
| − | Power series in real variables | + | Power series in real variables $ x = (x _ {1} \dots x _ {n} ) $, |
| + | $ n \geq 1 $, | ||
| + | are series of functions of the form | ||
| − | + | $$ \tag{8 } | |
| + | s(x) \ = \ \sum _ {| k | =0 } ^ \infty b _ {k} (x-a) ^ {k} , | ||
| + | $$ | ||
| − | where abbreviated notations are used, as in , and | + | where abbreviated notations are used, as in , and $ a = (a _ {1} \dots a _ {n} ) \in \mathbf R ^ {n} $ |
| + | is the centre of the series. If the series (8) converges absolutely in a parallelepipedon $ \Pi = \{ {x \in \mathbf R ^ {n} } : {| x _ {k} - a _ {k} | < r _ {k} ,\ k = 1 \dots n } \} $, | ||
| + | then it also converges absolutely in the polydisc $ U(a,\ r) = \{ {z \in \mathbf C ^ {n} } : {| z -a | < r } \} $, | ||
| + | $ r = (r _ {1} \dots r _ {n} ) $. | ||
| + | The sum of the series, $ s(x) $, | ||
| + | being an analytic function of the real variables $ x = (x _ {1} \dots x _ {n} ) $ | ||
| + | in $ \Pi $, | ||
| + | is continued analytically in the form of the power series | ||
| − | + | $$ \tag{9 } | |
| + | s(z) \ = \ \sum _ {\mid k \vDash0 } ^ \infty b _ {k} (z-a) ^ {k} | ||
| + | $$ | ||
| − | to the analytic function | + | to the analytic function $ s(z) $ |
| + | of the complex variables $ z = x+iy = (z _ {1} = x _ {1} + iy _ {1} \dots z _ {n} = x _ {n} + iy _ {n} ) $ | ||
| + | in $ U(a,\ r) $. | ||
| + | If $ D $ | ||
| + | is the domain of convergence of (9) in $ \mathbf C ^ {n} $( | ||
| + | complex variables $ z=x+iy $), | ||
| + | then its restriction $ \Delta $ | ||
| + | to $ \mathbf R ^ {n} $ | ||
| + | in the real variables $ x = (x _ {1} \dots x _ {n} ) $ | ||
| + | is the domain of convergence of (8), $ \Delta \subset D $. | ||
| + | In particular, when $ n=1 $, | ||
| + | $ D $ | ||
| + | is a disc of convergence and its restriction $ \Delta $ | ||
| + | is an interval of convergence on $ \mathbf R $, | ||
| + | and $ \Delta = \{ x \in \mathbf R ,\ a-r < x < a+r \} $, | ||
| + | where $ r $ | ||
| + | is the radius of convergence. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.V. Bitsadze, "Fundamentals of the theory of analytic functions of a complex variable" , Moscow (1972) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.I. Markushevich, "Theory of analytic functions of a complex variable" , '''1''' , Chelsea (1977) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.C. Titchmarsh, "The theory of functions" , Oxford Univ. Press (1979)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> L. Bieberbach, "Analytische Fortsetzung" , Springer (1955)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E. Landau, D. Gaier, "Darstellung und Begrundung einiger neuerer Ergebnisse der Funktionentheorie" , Springer, reprint (1986)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> B.V. Shabat, "Introduction of complex analysis" , '''1–2''' , Moscow (1985) (In Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> S. Bochner, W.T. Martin, "Several complex variables" , Princeton Univ. Press (1948)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> A.I. Yanushauskas, "Double series" , Novosibirsk (1980) (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.V. Bitsadze, "Fundamentals of the theory of analytic functions of a complex variable" , Moscow (1972) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.I. Markushevich, "Theory of analytic functions of a complex variable" , '''1''' , Chelsea (1977) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.C. Titchmarsh, "The theory of functions" , Oxford Univ. Press (1979)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> L. Bieberbach, "Analytische Fortsetzung" , Springer (1955)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E. Landau, D. Gaier, "Darstellung und Begrundung einiger neuerer Ergebnisse der Funktionentheorie" , Springer, reprint (1986)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> B.V. Shabat, "Introduction of complex analysis" , '''1–2''' , Moscow (1985) (In Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> S. Bochner, W.T. Martin, "Several complex variables" , Princeton Univ. Press (1948)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> A.I. Yanushauskas, "Double series" , Novosibirsk (1980) (In Russian)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | The approach to analytic functions via power series is the so-called Weierstrass approach. For a somewhat more abstract setting ( | + | The approach to analytic functions via power series is the so-called Weierstrass approach. For a somewhat more abstract setting ( $ \mathbf C $ |
| + | replaced by a suitable field) see [[#References|[a3]]], Chapts. 2–3 (cf. also [[Formal power series|Formal power series]]). | ||
| − | For | + | For $ \mathbf C ^ {n} $ |
| + | see [[#References|[a1]]]–[[#References|[a2]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Rudin, "Function theory in polydiscs" , Benjamin (1969)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Narasimhan, "Several complex variables" , Univ. Chicago Press (1971)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> K. Diederich, R. Remmert, "Funktionentheorie" , '''I''' , Springer (1972)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Rudin, "Function theory in polydiscs" , Benjamin (1969)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Narasimhan, "Several complex variables" , Univ. Chicago Press (1971)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> K. Diederich, R. Remmert, "Funktionentheorie" , '''I''' , Springer (1972)</TD></TR></table> | ||
Revision as of 11:57, 10 February 2020
Power series in one complex variable $ z $.
A series (representing a function) of the form
$$ \tag{1 } s(z) \ = \ \sum _ { k=0 } ^ \infty b _ {k} (z-a) ^ {k} , $$
where $ a $ is the centre, $ b _ {k} $ are the coefficients and $ b _ {k} (z-a) ^ {k} $ are the terms of the series. There exists a number $ r $, $ 0 \leq r \leq \infty $, called the radius of convergence of the power series (1) and determined by the Cauchy–Hadamard formula
$$ \tag{2 } r \ = \ \frac{1}{\lim\limits _ {k \rightarrow \infty } \ \sup \ | b _ {k} | ^ {1/k} } , $$
such that if $ | z-a | < r $ the series (1) converges absolutely, while if $ | z-a | > r $, it diverges (the Cauchy–Hadamard theorem). Accordingly, the disc $ D = \{ {z \in \mathbf C } : {| z-a | < r } \} $ in the complex $ z $- plane $ \mathbf C $ is called the disc of convergence of the power series (Fig. a).
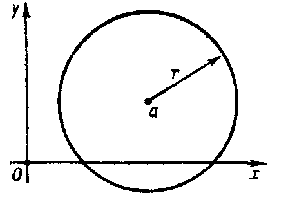
Figure: p074240a
When $ r=0 $, the disc of convergence degenerates to the single point $ z=a $, for example for the power series $ \sum _ {k=0} ^ \infty k!(z-a) ^ {k} $( this case is not of interest, and it is assumed from now on that $ r> 0 $). When $ r = \infty $, the disc of convergence coincides with the entire plane $ \mathbf C $, for example for the power series $ \sum _ {k=0} ^ \infty (z-a) ^ {k} /k! $. The set of convergence, i.e. the set of all points of convergence of the series (1), when $ 0 < r < \infty $, consists of the points of the disc of convergence $ D $ plus all, some or none of the points of the circle of convergence $ S = \{ {z \in \mathbf C } : {| z-a | = r } \} $. The disc of convergence in this case is the interior of the set of points of absolute convergence of the power series.
Within $ D $, i.e. on any compact set $ K \subset D $, the power series (1) converges absolutely and uniformly. Thus, the sum of the series, $ s(z) $, is defined, and is a regular analytic function at least inside $ D $. It has at least one singular point on $ S $ to which the sum $ s(z) $ cannot be analytically continued. There exist power series with exactly one singular point on $ S $; there also exist power series for which the entire circle $ S $ consists of singular points.
When $ r = \infty $, the series (1) either terminates, i.e. it is a polynomial,
$$ s(z) \ = \ \sum _ { k=0 } ^ { m } b _ {k} (z-a) ^ {k} , $$
or its sum is an entire transcendental function, which is regular in the entire place $ \mathbf C $ and which possesses an essential singular point at infinity.
Conversely, the very concept of analyticity of a function $ f(z) $ at a point $ a $ is based on the fact that in a neighbourhood of $ a $, $ f(z) $ can be expanded into a power series
$$ f(z) \ = \ \sum _ { k=0 } ^ \infty b _ {k} (z-a) ^ {k} , $$
which is the Taylor series for $ f(z) $, i.e. its coefficients are defined by the formulas
$$ b _ {k} \ = \ \frac{f ^ {\ (k) } (a) }{k!} . $$
Consequently, the uniqueness property of a power series is important: If the sum $ s(z) $ of the series (1) vanishes on an infinite set $ E \subset D $ with a limit point inside $ D $, then $ s(z) \equiv 0 $, and all $ b _ {k} = 0 $, $ k = 0,\ 1 ,\dots $. In particular, if $ s(z) = 0 $ in a neighbourhood of a certain point $ z _ {0} \in D $, then $ s(z) \equiv 0 $ and all $ b _ {k} = 0 $.
Thus, every power series is the Taylor series for its own sum.
Let there be another power series apart from (1):
$$ \tag{3 } \sigma (z) \ = \ \sum _ { k=0 } ^ \infty c _ {k} (z-a) ^ {k} $$
with the same centre $ a $ and with radius of convergence $ r _ {1} > 0 $. Then, at least inside the disc $ \Delta = \{ {z \in \mathbf C } : {| z-a | < \rho } \} $, where $ \rho = \mathop{\rm min} \{ r,\ r _ {1} \} $, the addition, subtraction and multiplication of the series (1) and (3) according to the following formulas hold:
$$ \tag{4 } \left . \begin{array}{c} s(z) \pm \sigma (z) \ = \ \sum _ { k=0 } ^ \infty (b _ {k} \pm c _ {k} )(z-a) ^ {k} , \\ s(z) \sigma (z) \ = \ \sum _ { k=0 } ^ \infty \left ( \sum _ { n=0 } ^ { k } b _ {n} c _ {k-n} \right ) (z-a) ^ {k} \end{array} \right \} . $$
The laws of commutativity, associativity and distributivity hold, whereby subtraction is the inverse operation of addition. Thus, the set of power series with positive radii of convergence and a fixed centre is a ring over the field $ \mathbf C $. If $ c _ {0} \neq 0 $, then division of power series is possible:
$$ \tag{5 } \frac{s(z)}{\sigma (z) } \ = \ \sum _ { k=0 } ^ \infty d _ {k} (z-a) ^ {k} , $$
where the coefficients $ d _ {k} $ are uniquely defined from the infinite system of equations
$$ \sum _ { n=0 } ^ { k } c _ {n} d _ {k-n} \ = \ a _ {k} ,\ \ k = 0,\ 1 ,\dots. $$
When $ c _ {0} \neq 0 $, $ r > 0 $ and $ r _ {1} > 0 $, the radius of convergence of (5) is also positive.
For the sake of simplicity, let $ a = \sigma (0) = c _ {0} = 0 $ in (1) and (3); the composite function $ s( \sigma (z)) $ will then be regular in a neighbourhood of the coordinate origin, and the process of expanding it into a power series is called substitution of a series in a series:
$$ \tag{6 } s( \sigma (z)) \ = \ \sum _ { n=0 } ^ \infty b _ {n} \left ( \sum _ { k=0 } ^ \infty c _ {k} z ^ {k} \right ) ^ {n} \ = \ \sum _ { m=0 } ^ \infty g _ {m} z ^ {m} . $$
The coefficient $ g _ {m} $ in (6) is obtained as the sum of the coefficients with the same index in the expansion of each of the functions $ b _ {n} ( \sigma (z)) ^ {n} $, while the latter expansions are obtained by $ n $- fold multiplication of the series for $ \sigma (z) $ by itself. The series (6) automatically converges when $ | z | < \rho $, where $ \rho $ is such that $ | \sigma (z) | < r $. Let $ a = \sigma (0) = c _ {0} = 0 $ again, and, moreover, let $ c _ {1} = \sigma ^ \prime (0) \neq 0 $, $ w = \sigma (z) $. The problem of constructing a series for the inverse function $ z = \phi (w) $, which under the given conditions is regular in a neighbourhood of the origin, is called inversion of the series (3). Its solution is the Lagrange series:
$$ z \ = \ \phi (w) \ = \ \sum _ { n=1 } ^ \infty \frac{1}{n!} \left ( \frac \zeta {\sigma ( \zeta ) } \right ) _ {\zeta =0 } ^ {(n)} w ^ {n} $$
(for a more general inversion problem see Bürmann–Lagrange series).
If the power series (1) converges at a point $ z _ {0} \neq a $, then it converges absolutely for all $ z $ for which $ | z-a | < | z _ {0} -a | $; this is the essence of Abel's first theorem. This theorem also makes it possible to establish the form of the domain of convergence of the series. Abel's second theorem provides a more detailed result: If the series (1) converges at the point $ z _ {0} = a + re ^ {i \theta _ {0} } $ on the circle of convergence $ S $, then
$$ \lim\limits _ {\rho \rightarrow r } \ s(a+ \rho e ^ {i \theta _ {0} } ) \ = \ s(z _ {0} ), $$
i.e. the sum of the series, $ s(z) $, at the point $ z _ {0} \in S $ has radial boundary value $ s(z _ {0} ) $ and, consequently, is continuous along the radius $ z = a + \rho ^ {i \theta _ {0} } $, $ 0 \leq \rho \leq r $; moreover, $ s(z) $ also has non-tangential boundary value $ s(z _ {0} ) $( cf. Angular boundary value). This theorem, dating back to 1827, can be seen as the first major result in the research into the boundary properties of power series. Inversion of Abel's second theorem without extra restrictions on the coefficients of the power series is impossible. However, if one assumes, for example, that $ b _ {k} = o(1/k) $, and if $ \lim\limits _ {\rho \rightarrow r } \ s(a+ \rho e ^ {i \theta _ {0} } ) = s _ {0} $ exists, then $ \sum _ {k=0} ^ \infty b _ {k} (z _ {0} -a) ^ {k} $ converges to $ s _ {0} $. This type of partial inversions of Abel's second theorem are called Tauberian theorems.
For other results relating to the boundary properties of power series and particularly to the location of singular points of power series, see Hadamard theorem; Analytic continuation; Boundary properties of analytic functions; Fatou theorem (see also –).
Power series in several complex variables $ z = (z _ {1} \dots z _ {n} ) $, $ n > 1 $, or multiple power series, are series (representing functions) of the form
$$ \tag{7 } s(z) \ = \ \sum _ {\mid k \vDash0 } ^ \infty b _ {k} (z-a) ^ {k\ } = $$
$$ = \ \sum _ {k _ {1} = 0 } ^ \infty \dots \sum _ {k _ {n} =0 } ^ \infty b _ {k _ {1} \dots k _ {n} } (z _ {1} - a _ {1} ) ^ {k _ {1} } \dots (z _ {n} - a _ {n} ) ^ {k _ {n} } , $$
where $ b _ {k} = b _ {k _ {1} \dots k _ {n} } $, $ (z-a) ^ {k} = (z _ {1} - a _ {1} ) ^ {k _ {1} } \dots (z _ {n} - a _ {n} ) ^ {k _ {n} } $, $ | k | = k _ {1} + \dots + k _ {n} $, and $ a = (a _ {1} \dots a _ {n} ) $, the centre of the series, is a point of the complex space $ \mathbf C ^ {n} $. The interior of the set of points of absolute convergence is called the domain of convergence $ D $ of the power series (7), but when $ n > 1 $, it does not have such a simple form as when $ n=1 $. A domain $ D $ of $ \mathbf C ^ {n} $ is the domain of convergence of a certain power series (7) if and only if $ D $ is a logarithmically-convex complete Reinhardt domain of $ \mathbf C ^ {n} $. If a certain point $ z ^ {0} \in D $, then the closure $ \overline{U}\; (a,\ r) $ of the polydisc $ U(a,\ r) = \{ {z \in \mathbf C ^ {n} } : {| z _ {v} - a _ {v} | < r _ {v} ,\ v = 1 \dots n } \} $, where $ r _ {v} = | z _ {v} ^ {0} - a _ {v} | $, $ r = (r _ {1} \dots r _ {n} ) $, also belongs to $ D $, and the series (7) converges absolutely and uniformly in $ \overline{U}\; (a,\ r) $( the analogue of Abel's first theorem). The polydisc $ U(a,\ r) $, $ r=(r _ {1} \dots r _ {n} ) $, is called the polydisc of convergence of the series (7), if $ U(a,\ r) \subset D $ and if in any larger polydisc $ \{ {z \in \mathbf C ^ {n} } : {| z _ {v} - a _ {v} | < r _ {v} ^ \prime } \} $, where $ r _ {v} ^ \prime \geq r _ {v} $, $ v = 1 \dots n $, and at least one inequality is strict, there are points at which the series (7) diverges. The radii $ r _ {v} $ of the polydisc of convergence are called conjugate radii of convergence, and satisfy a relation analogous to the Cauchy–Hadamard formula:
$$ \lim\limits _ {| k | \rightarrow \infty } \ \sup \ (| b _ {k} | r ^ {k} ) ^ {1/ | k | } \ = \ 1, $$
where $ | b _ {k} | = | b _ {k _ {1} } \dots b _ {k _ {n} } | $, $ r ^ {k} = r _ {1} ^ {k _ {1} } \dots r _ {n} ^ {k _ {n} } $. The domain of convergence $ D $ is exhausted by polydiscs of convergence. For example, for the series $ \sum _ {k=0} ^ \infty (z _ {1} z _ {2} ) ^ {k} $ the polydiscs of convergence take the form
$$ U \left ( 0,\ r _ {1} ,\ \frac{1}{r _ {1} } \right ) \ = \ \left \{ {z = (z _ {1} ,\ z _ {2} ) \in \mathbf C ^ {2} } : {| z _ {1} | < r _ {1} ,\ | z _ {2} | < \frac{1}{r _ {1} } } \right \} , $$
while the domain of convergence is $ D = \{ {z \in \mathbf C ^ {2} } : {| z _ {1} | \cdot | z _ {2} | < 1 } \} $( in Fig. bit is represented in the quadrant of absolute values).
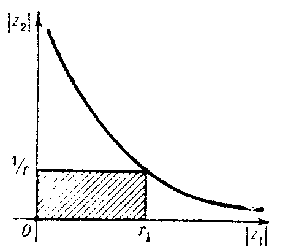
Figure: p074240b
The uniqueness property of power series is preserved in the sense that if $ s(z) = 0 $ in a neighbourhood of the point $ z ^ {0} $ in $ \mathbf C ^ {n} $( it is sufficient even in $ \mathbf R ^ {n} $, i.e. on a set $ \{ {z = x + iy \in \mathbf C ^ {n} } : {| x - \mathop{\rm Re} \ a | < r,\ y = \mathop{\rm Im} \ a } \} $), then $ s(z) \equiv 0 $ and all $ b _ {k} = 0 $.
Operations with multiple power series are carried out, broadly speaking, according to the same rules as when $ n=1 $. For other properties of multiple power series, see, for example, , .
Power series in real variables $ x = (x _ {1} \dots x _ {n} ) $, $ n \geq 1 $, are series of functions of the form
$$ \tag{8 } s(x) \ = \ \sum _ {| k | =0 } ^ \infty b _ {k} (x-a) ^ {k} , $$
where abbreviated notations are used, as in , and $ a = (a _ {1} \dots a _ {n} ) \in \mathbf R ^ {n} $ is the centre of the series. If the series (8) converges absolutely in a parallelepipedon $ \Pi = \{ {x \in \mathbf R ^ {n} } : {| x _ {k} - a _ {k} | < r _ {k} ,\ k = 1 \dots n } \} $, then it also converges absolutely in the polydisc $ U(a,\ r) = \{ {z \in \mathbf C ^ {n} } : {| z -a | < r } \} $, $ r = (r _ {1} \dots r _ {n} ) $. The sum of the series, $ s(x) $, being an analytic function of the real variables $ x = (x _ {1} \dots x _ {n} ) $ in $ \Pi $, is continued analytically in the form of the power series
$$ \tag{9 } s(z) \ = \ \sum _ {\mid k \vDash0 } ^ \infty b _ {k} (z-a) ^ {k} $$
to the analytic function $ s(z) $ of the complex variables $ z = x+iy = (z _ {1} = x _ {1} + iy _ {1} \dots z _ {n} = x _ {n} + iy _ {n} ) $ in $ U(a,\ r) $. If $ D $ is the domain of convergence of (9) in $ \mathbf C ^ {n} $( complex variables $ z=x+iy $), then its restriction $ \Delta $ to $ \mathbf R ^ {n} $ in the real variables $ x = (x _ {1} \dots x _ {n} ) $ is the domain of convergence of (8), $ \Delta \subset D $. In particular, when $ n=1 $, $ D $ is a disc of convergence and its restriction $ \Delta $ is an interval of convergence on $ \mathbf R $, and $ \Delta = \{ x \in \mathbf R ,\ a-r < x < a+r \} $, where $ r $ is the radius of convergence.
References
| [1] | A.V. Bitsadze, "Fundamentals of the theory of analytic functions of a complex variable" , Moscow (1972) (In Russian) |
| [2] | A.I. Markushevich, "Theory of analytic functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
| [3] | E.C. Titchmarsh, "The theory of functions" , Oxford Univ. Press (1979) |
| [4] | L. Bieberbach, "Analytische Fortsetzung" , Springer (1955) |
| [5] | E. Landau, D. Gaier, "Darstellung und Begrundung einiger neuerer Ergebnisse der Funktionentheorie" , Springer, reprint (1986) |
| [6] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
| [7] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1985) (In Russian) |
| [8] | S. Bochner, W.T. Martin, "Several complex variables" , Princeton Univ. Press (1948) |
| [9] | A.I. Yanushauskas, "Double series" , Novosibirsk (1980) (In Russian) |
Comments
The approach to analytic functions via power series is the so-called Weierstrass approach. For a somewhat more abstract setting ( $ \mathbf C $ replaced by a suitable field) see [a3], Chapts. 2–3 (cf. also Formal power series).
For $ \mathbf C ^ {n} $ see [a1]–[a2].
References
| [a1] | W. Rudin, "Function theory in polydiscs" , Benjamin (1969) |
| [a2] | R. Narasimhan, "Several complex variables" , Univ. Chicago Press (1971) |
| [a3] | K. Diederich, R. Remmert, "Funktionentheorie" , I , Springer (1972) |
Power series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Power_series&oldid=44404