Potential theory, abstract
The theory of potentials on abstract topological spaces. Abstract potential theory arose in the middle of the 20th century from the efforts to create a unified axiomatic method for treating a vast diversity of properties of the different potentials that are applied to solve problems of the theory of partial differential equations. The first sufficiently complete description of the axiomatics of "harmonic" functions (i.e. solutions of an admissible class of partial differential equations) and the corresponding potentials was given by M. Brelot (1957–1958, see [1]), but it was concerned only with elliptic equations. The extension of the theory to a wide class of parabolic equations was obtained by H. Bauer (1960–1963, see [3]). The probabilistic approach to abstract potential theory, the origins of which could be found already in the works of P. Lévy, J. Doob, G. Hunt, and others, turned out to be very fruitful.
To expose abstract potential theory, the notion of a harmonic space is of great help. Let 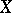 be a locally compact topological space. A sheaf of functions on
be a locally compact topological space. A sheaf of functions on 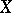 is a mapping
is a mapping 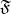 defined on the family of all open sets of
defined on the family of all open sets of 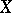 such that
such that
1) 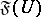 , for any open set
, for any open set 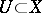 , is a family of functions
, is a family of functions 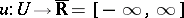 ;
;
2) if two open sets 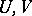 are such that
are such that  , then the restriction of any function from
, then the restriction of any function from 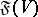 to
to 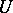 belongs to
belongs to 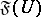 ;
;
3) if for any family 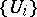 ,
, 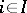 , of open sets
, of open sets 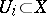 the restrictions to
the restrictions to 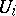 of some function
of some function  defined on
defined on 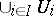 belong, for any
belong, for any 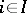 , to
, to 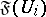 , then
, then 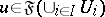 .
.
A sheaf of functions 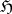 on
on 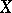 is called a harmonic sheaf if for any open set
is called a harmonic sheaf if for any open set 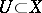 the family
the family 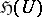 is a real vector space of continuous functions on
is a real vector space of continuous functions on 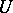 . A function
. A function  defined on some set
defined on some set 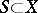 containing the open set
containing the open set 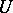 is called an
is called an 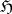 -function if the restriction
-function if the restriction 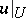 belongs to
belongs to 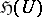 . A harmonic sheaf is non-degenerate at a point
. A harmonic sheaf is non-degenerate at a point 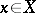 if in a neighbourhood of
if in a neighbourhood of  there exists an
there exists an 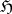 -function
-function  such that
such that 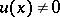 .
.
The real distinctions between the axiomatics of Bauer, Brelot and Doob can be characterized by the convergence properties of 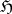 -functions.
-functions.
a) Bauer's convergence property states that if an increasing sequence of 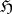 -functions is locally bounded on some open set
-functions is locally bounded on some open set 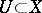 , then the limit function
, then the limit function  is an
is an 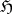 -function.
-function.
b) Doob's convergence property states that if a limit function  is finite on some dense set
is finite on some dense set 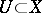 , then
, then  is an
is an 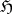 -function.
-function.
c) Brelot's convergence property states that if the limit function  of an increasing sequence of
of an increasing sequence of 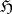 -functions on some domain
-functions on some domain 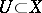 is finite at a point
is finite at a point 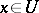 , then
, then  is an
is an 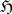 -function.
-function.
If the space 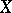 is locally connected, the implications c)
is locally connected, the implications c)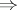 b)
b)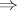 a) hold.
a) hold.
A sheaf of functions 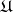 on
on 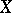 is called a hyperharmonic sheaf if for any open set
is called a hyperharmonic sheaf if for any open set 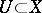 the family
the family 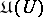 is a convex cone of lower semi-continuous functions
is a convex cone of lower semi-continuous functions 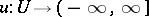 ; a
; a 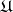 -function is defined in a similar way as an
-function is defined in a similar way as an  -function. The mapping
-function. The mapping 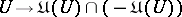 is a harmonic sheaf, denoted by
is a harmonic sheaf, denoted by 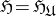 and generated by the sheaf
and generated by the sheaf 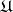 ; hereafter, only this harmonic sheaf will be used.
; hereafter, only this harmonic sheaf will be used.
Let on the boundary 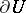 of an open set
of an open set  a continuous function
a continuous function  with compact support be given. The hyperharmonic sheaf
with compact support be given. The hyperharmonic sheaf 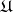 allows one to construct a generalized solution of the Dirichlet problem for certain open sets in the class of corresponding
allows one to construct a generalized solution of the Dirichlet problem for certain open sets in the class of corresponding  -functions by the Perron method. Let
-functions by the Perron method. Let 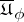 be a family of lower semi-continuous
be a family of lower semi-continuous 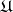 -functions
-functions  , bounded from below on
, bounded from below on 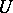 , positive outside some compact set and such that
, positive outside some compact set and such that
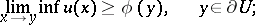 |
define 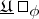 by
by 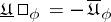 . Now, let,
. Now, let,
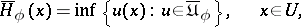 |
and let 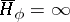 if
if 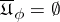 . Similarly,
. Similarly,
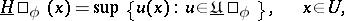 |
or 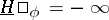 . A function is called resolutive if for this function
. A function is called resolutive if for this function 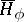 and
and 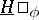 coincide,
coincide, 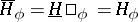 , and if
, and if 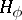 is an
is an 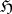 -function; this function
-function; this function 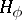 is a generalized solution of the Dirichlet problem in the class of
is a generalized solution of the Dirichlet problem in the class of 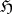 -functions. An open set
-functions. An open set 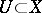 is resolutive with respect to
is resolutive with respect to 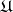 if every finite continuous function with compact support on
if every finite continuous function with compact support on 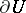 is resolutive. For a resolutive set
is resolutive. For a resolutive set 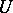 the mapping
the mapping 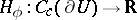 is a positive linear functional, hence it determines a positive measure
is a positive linear functional, hence it determines a positive measure 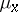 ,
, 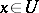 , which is called the harmonic measure on
, which is called the harmonic measure on 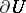 (or on
(or on 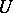 ) at the point
) at the point  (with respect to
(with respect to 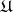 ).
).
A locally compact space 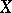 with a hyperharmonic sheaf
with a hyperharmonic sheaf  turns into a harmonic space if the four corresponding axioms (see Harmonic space) hold; moreover, in the convergence axiom the property is understood in the sense of Bauer.
turns into a harmonic space if the four corresponding axioms (see Harmonic space) hold; moreover, in the convergence axiom the property is understood in the sense of Bauer.
Often (it is like this in classical examples) one takes as a basis the harmonic sheaf 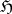 , and the axiom of completeness serves then as a definition of a hyperharmonic sheaf. For instance, the Euclidean space
, and the axiom of completeness serves then as a definition of a hyperharmonic sheaf. For instance, the Euclidean space 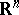 ,
, 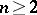 , together with the sheaf of classical solutions of the Laplace equation or of the heat equation as
, together with the sheaf of classical solutions of the Laplace equation or of the heat equation as 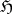 , is a harmonic space. A harmonic space is locally connected, does not contain isolated points and has a basis consisting of connected resolutive sets (resolutive domains).
, is a harmonic space. A harmonic space is locally connected, does not contain isolated points and has a basis consisting of connected resolutive sets (resolutive domains).
An open set  in a harmonic space
in a harmonic space 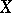 with the restriction
with the restriction 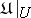 as hyperharmonic sheaf is a harmonic subspace of
as hyperharmonic sheaf is a harmonic subspace of 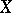 . A hyperharmonic function
. A hyperharmonic function  on
on 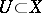 is called a superharmonic function if for any relatively compact resolutive set
is called a superharmonic function if for any relatively compact resolutive set 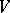 with
with 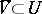 , the greatest minorant
, the greatest minorant 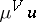 is harmonic,
is harmonic, 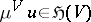 . Many properties of classical superharmonic functions (see Subharmonic function) also hold in this case. A potential is a positive superharmonic function
. Many properties of classical superharmonic functions (see Subharmonic function) also hold in this case. A potential is a positive superharmonic function  such that its greatest harmonic minorant on
such that its greatest harmonic minorant on 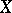 is identically equal to zero. A harmonic space
is identically equal to zero. A harmonic space 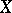 is called a
is called a  -harmonic (or
-harmonic (or 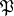 -harmonic) space if for any point
-harmonic) space if for any point 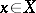 there exists a positive superharmonic function
there exists a positive superharmonic function  (a potential
(a potential  , respectively) on
, respectively) on 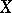 such that
such that 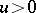 . Any open set in a
. Any open set in a 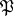 -harmonic space is resolutive.
-harmonic space is resolutive.
Taking a harmonic sheaf 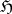 as basis and defining the corresponding hyperharmonic sheaf
as basis and defining the corresponding hyperharmonic sheaf 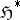 by the axiom of completeness, one obtains the Bauer space, which coincides with the harmonic space for
by the axiom of completeness, one obtains the Bauer space, which coincides with the harmonic space for 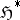 . If the harmonic sheaf
. If the harmonic sheaf 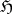 , for any open set
, for any open set 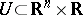 , consists of the solutions
, consists of the solutions 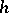 of the heat equation
of the heat equation 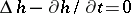 , then
, then 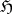 has the Doob convergence property and
has the Doob convergence property and 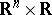 together with this sheaf
together with this sheaf 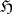 is a (Bauer)
is a (Bauer) 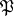 -space. Here,
-space. Here,  is a superharmonic function of class
is a superharmonic function of class 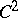 if and only if
if and only if 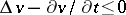 .
.
A Brelot space is characterized by the following conditions: 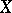 does not have isolated points and is locally connected; the regular sets with respect to
does not have isolated points and is locally connected; the regular sets with respect to 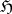 form a base of
form a base of 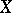 (regularity means resolutivity of the classical Dirichlet problem in the class
(regularity means resolutivity of the classical Dirichlet problem in the class 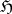 ); and
); and 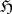 has the Brelot convergence property. The Brelot spaces form a proper subclass of the so-called elliptic harmonic spaces (see [4]), i.e. the elliptic Bauer spaces. If the harmonic sheaf
has the Brelot convergence property. The Brelot spaces form a proper subclass of the so-called elliptic harmonic spaces (see [4]), i.e. the elliptic Bauer spaces. If the harmonic sheaf 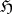 , for any open set
, for any open set 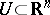 ,
,  , consists of the solutions
, consists of the solutions  of the Laplace equation
of the Laplace equation 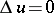 , then
, then 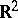 together with this sheaf is a Brelot
together with this sheaf is a Brelot 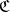 -space, and
-space, and 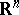 for
for 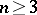 is a Brelot
is a Brelot 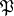 -space. Here,
-space. Here,  is a hyperharmonic function of class
is a hyperharmonic function of class 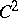 if and only if
if and only if 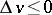 .
.
A point 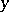 of the boundary
of the boundary 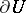 of a resolutive set
of a resolutive set 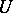 is called a regular boundary point if for any finite continuous function
is called a regular boundary point if for any finite continuous function 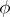 on
on 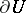 the following limit relation holds:
the following limit relation holds:
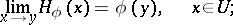 |
otherwise 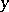 is called an irregular boundary point. Let
is called an irregular boundary point. Let 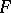 be a filter on
be a filter on 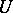 converging to
converging to 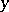 . A strictly-positive hyperharmonic function
. A strictly-positive hyperharmonic function  defined on the intersection of
defined on the intersection of 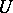 with some neighbourhood of
with some neighbourhood of 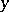 and converging to
and converging to  along
along 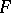 is called a barrier of the filter
is called a barrier of the filter 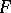 . If for a relatively compact resolutive set
. If for a relatively compact resolutive set 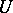 in a
in a 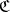 -harmonic space all filters that converge to points
-harmonic space all filters that converge to points 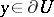 have barriers, then
have barriers, then 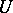 is a regular set, i.e. all its boundary points are regular. If
is a regular set, i.e. all its boundary points are regular. If 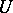 is a relatively compact open set in a
is a relatively compact open set in a 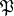 -harmonic space on which there exists a strictly-positive hyperharmonic function converging to
-harmonic space on which there exists a strictly-positive hyperharmonic function converging to  at each point
at each point 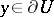 , then
, then  is a regular set.
is a regular set.
Besides studies concerning resolutivity and regularity in the Dirichlet problem, the following problems are of major interest in abstract potential theory: the theory of capacity of point sets in harmonic spaces 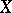 ; the theory of balayage (see Balayage method) for functions and measures on
; the theory of balayage (see Balayage method) for functions and measures on 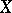 ; and the theory of integral representations of positive superharmonic functions on
; and the theory of integral representations of positive superharmonic functions on  generalizing the Martin representations (see Martin boundary in potential theory).
generalizing the Martin representations (see Martin boundary in potential theory).
Already at the beginning of the 20th century it became evident that potential theory is closely related to certain concepts of probability theory such as Brownian motion; Wiener process; and Markov process. For instance, the probability that the trajectory of a Brownian motion in a domain  starting at the point
starting at the point 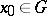 will hit for the first time the boundary
will hit for the first time the boundary 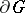 on a (Borel) set
on a (Borel) set 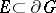 is exactly the harmonic measure of
is exactly the harmonic measure of 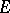 at
at 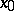 ; the polar sets (cf. Polar set) on
; the polar sets (cf. Polar set) on 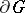 are the sets that are almost-certainly not hit by the trajectory. Later on, probabilistic methods contributed to a more profound understanding of certain ideas from potential theory and led to a series of new results; on the other hand, the potential-theoretic approach led to a better understanding of the results of probability theory and also leads to new results in it.
are the sets that are almost-certainly not hit by the trajectory. Later on, probabilistic methods contributed to a more profound understanding of certain ideas from potential theory and led to a series of new results; on the other hand, the potential-theoretic approach led to a better understanding of the results of probability theory and also leads to new results in it.
Let 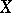 be a locally compact space with a countable base, let
be a locally compact space with a countable base, let  and
and 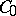 be the classes of finite continuous functions on
be the classes of finite continuous functions on 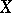 , respectively, with compact support and convergent to zero at infinity. A measure kernel
, respectively, with compact support and convergent to zero at infinity. A measure kernel 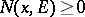 is a (Borel) function in
is a (Borel) function in 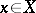 for every relatively compact (Borel) set
for every relatively compact (Borel) set 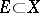 . Using
. Using 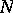 , to each function
, to each function 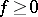 ,
,  , corresponds a potential function
, corresponds a potential function
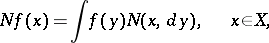 |
and to a measure 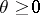 corresponds a potential measure
corresponds a potential measure
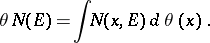 |
The identity kernel 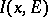 vanishes when
vanishes when 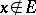 and is equal to
and is equal to  when
when 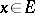 , it changes neither
, it changes neither 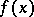 nor
nor 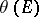 . For instance, in the Euclidean space
. For instance, in the Euclidean space 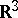 the kernel
the kernel
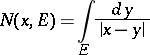 |
determines the Newton potential 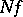 with density
with density 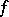 , and
, and 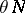 is the measure with density equal to the density of the Newton potential of the measure
is the measure with density equal to the density of the Newton potential of the measure 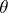 (see Potential theory).
(see Potential theory).
A product kernel has the form
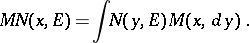 |
A family of kernels 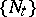 ,
, 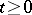 , with the composition law
, with the composition law 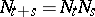 is a one-parameter semi-group. A kernel
is a one-parameter semi-group. A kernel  satisfies the complete maximum principle if for any
satisfies the complete maximum principle if for any  from
from 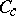 and
and  the inequality
the inequality 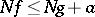 on the set where
on the set where 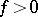 leads to this inequality everywhere on
leads to this inequality everywhere on 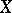 . The principal theorem in this theory is Hunt's theorem, which in its simplest version is the following: If the image of
. The principal theorem in this theory is Hunt's theorem, which in its simplest version is the following: If the image of 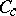 under a transformation
under a transformation 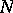 is dense in
is dense in 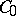 and if
and if 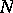 satisfies the complete maximum principle, then there exists a semi-group
satisfies the complete maximum principle, then there exists a semi-group 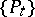 ,
, 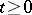 , such that
, such that
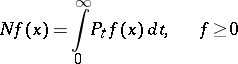 |
(a Feller semi-group); moreover, 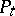 transforms
transforms 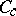 into
into 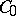 ;
; 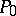 is the identity kernel;
is the identity kernel;  ,
, 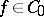 , locally uniform; and
, locally uniform; and 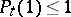 . A measurable function
. A measurable function 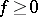 is called an excessive function with respect to the semi-group
is called an excessive function with respect to the semi-group 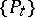 if always
if always 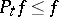 and if
and if 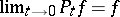 ; if
; if  , then
, then 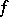 is called an invariant function. The corresponding formulas are also valid for the potential measure
is called an invariant function. The corresponding formulas are also valid for the potential measure 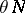 .
.
The theory of Hunt (1957–1958) outlined above has a direct probabilistic sense. Let on 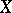 be given some
be given some 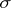 -algebra
-algebra 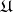 of Borel sets and a probability measure
of Borel sets and a probability measure 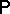 . A random variable
. A random variable 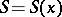 is a
is a 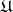 -measurable mapping of
-measurable mapping of  into the state space
into the state space 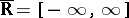 . The family of random variables
. The family of random variables 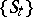 ,
, 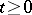 , is a Markov process (for which
, is a Markov process (for which 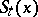 is the trajectory of a point
is the trajectory of a point 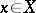 ) if for any
) if for any 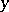 ,
, 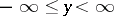 , there exists a probability measure
, there exists a probability measure 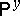 on
on  such that a)
such that a) 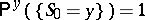 ; b)
; b) 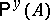 ,
, 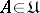 , is a Borel function of
, is a Borel function of 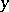 ; and c) the form of a trajectory passing through
; and c) the form of a trajectory passing through 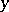 at a moment
at a moment  , for
, for 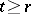 , is independent of the positions of the points preceding it. In such Markov processes the semi-groups
, is independent of the positions of the points preceding it. In such Markov processes the semi-groups 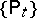 are interpreted as semi-groups of measures
are interpreted as semi-groups of measures
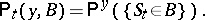 |
Studies of excessive and invariant functions with respect to the semi-groups 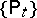 are of great importance.
are of great importance.
On the other hand, if 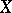 is a
is a 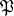 -harmonic space with a countable base, then one can always choose on it a potential kernel to meet the requirements of Hunt's theorem; in this case the excessive functions of the associated semi-group are precisely the non-negative hyperharmonic functions. Hunt's theorem can be also generalized for some types of Bauer spaces (see [4], [7]).
-harmonic space with a countable base, then one can always choose on it a potential kernel to meet the requirements of Hunt's theorem; in this case the excessive functions of the associated semi-group are precisely the non-negative hyperharmonic functions. Hunt's theorem can be also generalized for some types of Bauer spaces (see [4], [7]).
Other concepts from abstract potential theory, such as, for example, balayage, polar and thin sets, also have their probabilistic interpretation within the framework of the general theory of random processes; this facilitates studies of the latter. On the other hand, the potential-theoretic approach to a series of concepts, such as, for example, martingales, which are beyond the limits of Markov processes, turned out to be of great importance.
References
| [1] | M. Brélot, "Lectures on potential theory" , Tata Inst. (1960) |
| [2] | M. Brelot, "Les étapes et les aspects multiples de la théorie du potentiel" Enseign. Math. , 18 : 1 (1972) pp. 1–36 |
| [3] | H. Bauer, "Harmonische Räume und ihre Potentialtheorie" , Springer (1966) |
| [4] | C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972) |
| [5] | P.A. Meyer, "Probability and potentials" , Blaisdell (1966) |
| [6a] | G.A. Hunt, "Markov processes and potentials, I" Illinois J. Math. , 1 (1957) pp. 44–93 |
| [6b] | G.A. Hunt, "Markov processes and potentials, II" Illinois J. Math. , 1 (1957) pp. 316–362 |
| [6c] | G.A. Hunt, "Markov processes and potentials, III" Illinois J. Math. , 2 (1958) pp. 151–213 |
| [7] | R.M. Blumenthal, R.K. Getoor, "Markov processes and potential theory" , Acad. Press (1968) |
Comments
Abstract potential theory is also called axiomatic potential theory.
A measure kernel 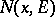 is also defined as a (
is also defined as a (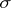 -additive, non-negative) measure in
-additive, non-negative) measure in 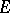 , and
, and  can be defined whenever
can be defined whenever  is Borel and non-negative; in the article above,
is Borel and non-negative; in the article above, 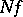 is assumed finite if
is assumed finite if 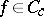 . By definition, a Feller semi-group
. By definition, a Feller semi-group 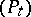 transforms
transforms 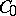 to
to 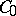 ,
,  is the identity kernel and for
is the identity kernel and for 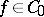 the transformation
the transformation 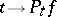 is continuous at 0 for the uniform topology. If
is continuous at 0 for the uniform topology. If 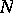 and
and 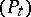 are related by Hunt's theorem,
are related by Hunt's theorem, 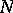 is called the potential kernel of the Feller semi-group
is called the potential kernel of the Feller semi-group 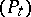 , and for any non-negative Borel function
, and for any non-negative Borel function 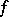 the potential
the potential 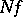 of
of 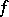 is an excessive function with respect to the semi-group
is an excessive function with respect to the semi-group 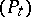 . One can define analogously excessive measures and potential measures, and their study is also of great importance. The passage in the article on the definition of a Markov process is somewhat misleading: the
. One can define analogously excessive measures and potential measures, and their study is also of great importance. The passage in the article on the definition of a Markov process is somewhat misleading: the 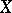 equipped with the
equipped with the 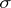 -algebra
-algebra 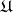 has to be replaced by an extraneous measurable space, say
has to be replaced by an extraneous measurable space, say 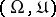 , and the state space
, and the state space  by the locally compact space
by the locally compact space 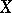 where the Hunt kernel
where the Hunt kernel 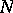 is defined, so that in the equality
is defined, so that in the equality 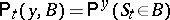 one has
one has 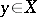 and
and 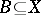 (and Borel). See Markov process.
(and Borel). See Markov process.
Around 1959, A. Beurling and J. Deny introduced another branch of abstract potential theory: the notion of Dirichlet space, an axiomatization of the theory of the Dirichlet integral. See [a3].
Several abstract theories have been introduced, aimed at a unification of different branches of potential theory, e.g. the theory of balayage spaces, cf. [a2], and the theory of 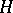 -cones, cf. [a1]. Both concepts use a convex cone of functions (the positive hyperharmonic functions, e.g.), satisfying some convergence properties, a Riesz property and a separation property as their main tool. See also [a4] for short surveys.
-cones, cf. [a1]. Both concepts use a convex cone of functions (the positive hyperharmonic functions, e.g.), satisfying some convergence properties, a Riesz property and a separation property as their main tool. See also [a4] for short surveys.
References
| [a1] | N. Boboc, Gh. Bucur, A. Cornea, "Order and convexity in potential theory: 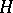 -cones" , Springer (1981) -cones" , Springer (1981) |
| [a2] | J. Bliedtner, W. Hansen, "Potential theory. An analytic and probabilistic approach to balayage" , Springer (1986) |
| [a3] | M. Fukushima, "Dirichlet forms and Markov processes" , North-Holland (1980) |
| [a4] | J. Král (ed.) J. Lukeš (ed.) J. Veselý (ed.) , Potential theory. Survey and problems (Prague, 1987) , Lect. notes in math. , 1344 , Springer (1988) |
| [a5] | M. Brelot (ed.) H. Bauer (ed.) J.-M. Bony (ed.) J. Deny (ed.) G. Mokobodzki (ed.) , Potential theory (CIME, Stresa, 1969) , Cremonese (1970) |
| [a6] | C. Dellacherie, P.A. Meyer, "Probabilities and potential" , C , North-Holland (1988) (Translated from French) |
| [a7] | F.Y. Maeda, "Dirichlet integrals on harmonic spaces" , Lect. notes in math. , 803 , Springer (1980) |
| [a8] | M. Röckner, "Markov property of generalized fields and axiomatic potential theory" Math. Ann. , 264 (1983) pp. 153–177 |
Potential theory, abstract. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Potential_theory,_abstract&oldid=14793