Potential of a mass distribution
An expression of the form
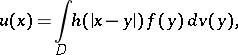 | (*) |
where  is a bounded domain in a Euclidean space
is a bounded domain in a Euclidean space 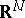 ,
, 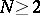 , bounded by a closed Lyapunov surface
, bounded by a closed Lyapunov surface 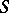 (a curve for
(a curve for 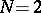 , cf. Lyapunov surfaces and curves),
, cf. Lyapunov surfaces and curves),  is the fundamental solution of the Laplace operator:
is the fundamental solution of the Laplace operator:
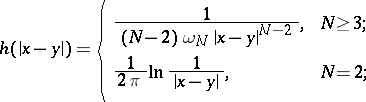 |
where  is the area of the unit sphere in
is the area of the unit sphere in 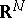 ,
, 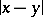 is the distance between the points
is the distance between the points  and
and 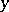 , and
, and 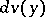 is the volume element in
is the volume element in 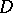 .
.
If  , then the potential is defined for all
, then the potential is defined for all 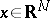 and
and  . In the complementary domain
. In the complementary domain  , the function
, the function  then has derivatives of all orders and satisfies the Laplace equation:
then has derivatives of all orders and satisfies the Laplace equation: 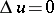 , that is, is a harmonic function; for
, that is, is a harmonic function; for 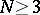 this function is regular at infinity,
this function is regular at infinity, 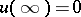 . In
. In 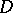 the potential
the potential  belongs to the class
belongs to the class  and satisfies the Poisson equation:
and satisfies the Poisson equation: 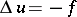 .
.
These properties can be generalized in various ways. For example, if 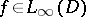 , then
, then 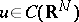 ,
, 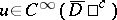 ,
, 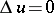 in
in 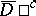 ,
,  has generalized second derivatives in
has generalized second derivatives in 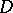 , and the Poisson equation
, and the Poisson equation  is satisfied almost-everywhere in
is satisfied almost-everywhere in 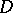 . Properties of potentials of an arbitrary Radon measure
. Properties of potentials of an arbitrary Radon measure 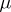 concentrated on an
concentrated on an 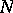 -dimensional domain
-dimensional domain 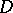 have also been studied:
have also been studied:
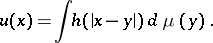 |
Here again 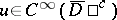 and
and 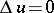 in
in 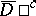 ,
, 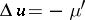 almost-everywhere in
almost-everywhere in 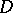 , where
, where 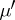 is the derivative of
is the derivative of 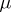 with respect to Lebesgue measure in
with respect to Lebesgue measure in 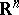 . In definition (*) the fundamental solution of the Laplace operator may be replaced by an arbitrary Levi function (see [2]) for a general second-order elliptic operator
. In definition (*) the fundamental solution of the Laplace operator may be replaced by an arbitrary Levi function (see [2]) for a general second-order elliptic operator 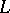 with variable coefficients of class
with variable coefficients of class 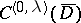 ; then the properties listed above still hold with
; then the properties listed above still hold with 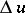 replaced by
replaced by  (see [2]–[4]).
(see [2]–[4]).
Potentials of mass distributions are applied in the solution of boundary value problems for elliptic partial differential equations (see [2]–[5]).
For the solution of boundary value problems for parabolic partial differential equations the concept of a heat potential of the form
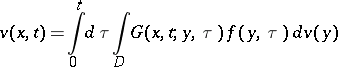 |
is used, where 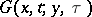 is a fundamental solution of the heat equation in
is a fundamental solution of the heat equation in 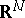 :
:
 |
and  is the density. The function
is the density. The function  and its generalizations to the case of an arbitrary second-order parabolic partial differential equation have properties similar to those given above for
and its generalizations to the case of an arbitrary second-order parabolic partial differential equation have properties similar to those given above for  (see [3]–[6]).
(see [3]–[6]).
References
| [1] | N.M. Günter, "Potential theory and its applications to basic problems of mathematical physics" , F. Ungar (1967) (Translated from French) |
| [2] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
| [3] | A.N. [A.N. Tikhonov] Tichonoff, A.A. Samarskii, "Differentialgleichungen der mathematischen Physik" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [4] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian) |
| [5] | A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) |
| [6] | A.V. Bitsadze, "Boundary value problems for second-order elliptic equations" , North-Holland (1968) (Translated from Russian) |
Comments
A Levi function of a linear partial differential equation is also called a fundamental solution of this equation, or a parametrix of this equation. This function is named after E.E. Levi, who anticipated [a1], [a2] what is known today as the parametrix method.
See also Potential theory; Logarithmic potential; Newton potential; Non-linear potential; Riesz potential; Bessel potential.
References
| [a1] | E.E. Levi, "Sulle equazioni lineari alle derivate parziali totalmente ellittiche" Rend. R. Acc. Lincei, Classe Sci. (V) , 16 (1907) pp. 932–938 |
| [a2] | E.E. Levi, "Sulle equazioni lineari totalmente ellittiche alle derivate parziali" Rend. Circ. Mat. Palermo , 24 (1907) pp. 275–317 |
| [a3] | O.D. Kellogg, "Foundations of potential theory" , F. Ungar (1929) (Re-issue: Springer, 1967) |
Potential of a mass distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Potential_of_a_mass_distribution&oldid=16403