Poisson Lie group
A Lie group 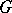 with a Poisson structure
with a Poisson structure  which is compatible with the group multiplication, i.e., the multiplication
which is compatible with the group multiplication, i.e., the multiplication 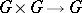 is a Poisson mapping, where
is a Poisson mapping, where 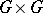 is the product Poisson manifold (cf. Poisson algebra).
is the product Poisson manifold (cf. Poisson algebra).
The corresponding infinitesimal object is a Lie bialgebra (see Quantum groups) 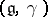 , called the tangent Lie bialgebra of
, called the tangent Lie bialgebra of 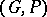 . Here,
. Here, 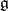 is the Lie algebra of the Lie group
is the Lie algebra of the Lie group 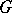 and the linear mapping
and the linear mapping 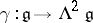 is defined to be the linearization of
is defined to be the linearization of 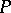 at the identity of the group; it is a Lie-algebra
at the identity of the group; it is a Lie-algebra 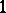 -cocycle with respect to the adjoint action (because of the compatibility condition) and a Lie cobracket, i.e., its transpose is a Lie bracket on the dual
-cocycle with respect to the adjoint action (because of the compatibility condition) and a Lie cobracket, i.e., its transpose is a Lie bracket on the dual  of
of 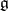 . Conversely, any Lie bialgebra can be integrated to a unique (up to isomorphism) connected and simply connected Poisson Lie group.
. Conversely, any Lie bialgebra can be integrated to a unique (up to isomorphism) connected and simply connected Poisson Lie group.
To each Lie bialgebra structure on  there corresponds a Lie bialgebra structure
there corresponds a Lie bialgebra structure 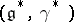 on
on 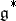 , called the dual of
, called the dual of 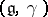 , and a Lie bialgebra structure on
, and a Lie bialgebra structure on 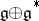 , called the double of
, called the double of 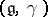 . Therefore, each Poisson Lie group
. Therefore, each Poisson Lie group 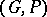 has a dual
has a dual 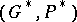 , and a double, with underlying manifold
, and a double, with underlying manifold 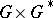 . There are Poisson actions of
. There are Poisson actions of 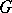 on
on 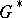 , and of
, and of 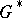 on
on 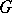 , called the dressing actions. The symplectic leaves of the Poisson manifold
, called the dressing actions. The symplectic leaves of the Poisson manifold 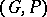 are the orbits of the dressing action of
are the orbits of the dressing action of 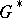 .
.
An element 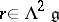 is called a solution of the classical (respectively, generalized) Yang–Baxter equation if the algebraic Schouten bracket
is called a solution of the classical (respectively, generalized) Yang–Baxter equation if the algebraic Schouten bracket 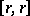 of
of  with itself vanishes (respectively, is ad-invariant). A solution
with itself vanishes (respectively, is ad-invariant). A solution 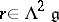 of the classical Yang–Baxter equation is also called a triangular
of the classical Yang–Baxter equation is also called a triangular  -matrix. A solution of the generalized Yang–Baxter equation defines a Lie bialgebra structure on
-matrix. A solution of the generalized Yang–Baxter equation defines a Lie bialgebra structure on 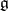 , and a Poisson Lie structure on any Lie group
, and a Poisson Lie structure on any Lie group 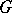 with Lie algebra
with Lie algebra 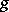 . In particular, a triangular
. In particular, a triangular  -matrix defines both a left-invariant and a right-invariant Poisson structure on
-matrix defines both a left-invariant and a right-invariant Poisson structure on 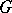 whose difference is a Poisson Lie structure. An element
whose difference is a Poisson Lie structure. An element 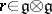 with an invariant symmetric part
with an invariant symmetric part  is called a quasi-triangular
is called a quasi-triangular  -matrix if it satisfies
-matrix if it satisfies 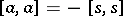 , where
, where  is its skew-symmetric part and
is its skew-symmetric part and 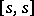 is the ad-invariant element in
is the ad-invariant element in 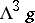 , defined by
, defined by  , for
, for 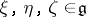 . Thus, the skew-symmetric part of a quasi-triangular
. Thus, the skew-symmetric part of a quasi-triangular  -matrix defines a Poisson Lie structure on
-matrix defines a Poisson Lie structure on 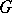 . The equation
. The equation 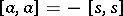 , which reduces to
, which reduces to 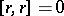 when
when 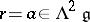 , is variously called the classical Yang–Baxter equation, for
, is variously called the classical Yang–Baxter equation, for 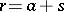 , or the modified Yang–Baxter equation, for
, or the modified Yang–Baxter equation, for  . It is usually written in the form
. It is usually written in the form 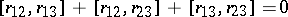 .
.
Examples are: trivial Poisson Lie groups, where 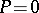 , with as dual Poisson Lie group the dual of the Lie algebra with its linear Poisson structure (also called the Kirillov–Kostant–Souriau Poisson structure), and with as double the cotangent bundle of
, with as dual Poisson Lie group the dual of the Lie algebra with its linear Poisson structure (also called the Kirillov–Kostant–Souriau Poisson structure), and with as double the cotangent bundle of 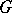 ; the simple Lie groups with the standard quasi-triangular
; the simple Lie groups with the standard quasi-triangular  -matrix; and the compact Lie groups with their Bruhat–Poisson structure.
-matrix; and the compact Lie groups with their Bruhat–Poisson structure.
It should be noted that the algebraic concept of a Lie bialgebra and the differential-geometric notion of a Poisson Lie group were first encountered as the classical limits of quantum objects participating in the quantum inverse scattering theory for integrable systems. (Thus, the classical Yang–Baxter equation is the classical limit of the quantum Yang–Baxter equation.) Conversely, the quantization problem is the problem of associating a quantum group to a given Poisson Lie group, i.e., of finding non-commutative deformations of its commutative algebra of functions, which is a Poisson–Hopf algebra (a Poisson algebra with a Hopf algebra structure such that the comultiplication is a morphism of Poisson algebras). Dually, quantum groups are also obtained as non-co-commutative deformations of the universal enveloping algebras of Lie bialgebras, which are co-commutative co-Poisson–Hopf algebras.
References
| [a1] | V.G. Drinfeld, "Hamiltonian structures on Lie groups, Lie bialgebras and the geometric meaning of the classical Yang–Baxter equation" Soviet Math. Dokl. , 27 (1983) pp. 68–71 (In Russian) |
| [a2] | M.A. Semenov-Tian-Shansky, "Dressing transformations and Poisson group actions" Publ. RIMS Kyoto Univ. , 21 (1985) pp. 1237–1260 |
| [a3] | V.G. Drinfeld, "Quantum groups" , Proc. Intern. Congress Mathematicians, Berkeley 1966 , 1 , Amer. Math. Soc. (1987) pp. 798–820 |
| [a4] | Y. Kosmann-Schwarzbach, F. Magri, "Poisson–Lie groups and complete integrability" Ann. Inst. Henri Poincaré, Phys. Th. A , 49 (1988) pp. 433–460 |
| [a5] | J.-H. Lu, A. Weinstein, "Poisson Lie groups, dressing transformations, and Bruhat decompositions" J. Diff. Geom. , 31 (1990) pp. 501–526 |
| [a6] | S. Majid, "Matched pairs of Lie groups associated to solutions of the Yang–Baxter equation" Pacific J. Math. , 141 (1990) pp. 311–332 |
| [a7] | V. Chari, A. Pressley, "A guide to quantum groups" , Cambridge Univ. Press (1994) pp. Chapts. 1–3 |
| [a8] | A.G. Reyman, M.A. Semenov-Tian-Shansky, "Integrable systems II" V.I. Arnold (ed.) S.P. Novikov (ed.) , Dynamical Systems VII , Springer (1994) pp. 116–259 |
| [a9] | I. Vaisman, "Lectures on the geometry of Poisson manifolds" , Progress in Math. , 118 , Birkhäuser (1994) pp. Chapt. 10 |
| [a10] | A.G. Reyman, "Poisson structures related to quantum groups" L. Castellani (ed.) J. Wess (ed.) , Quantum Groups and their Applications in Physics, Internat. School Enrico Fermi (Varenna 1994) , IOS , Amsterdam (1996) pp. 407–443 |
Poisson Lie group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poisson_Lie_group&oldid=14191