Point of inflection
A point $ M $
on a planar curve having the following properties: at $ M $
the curve has a unique tangent, and within a small neighbourhood around $ M $
the curve lies within one pair of vertical angles formed by the tangent and the normal (Fig. a). normal tangent
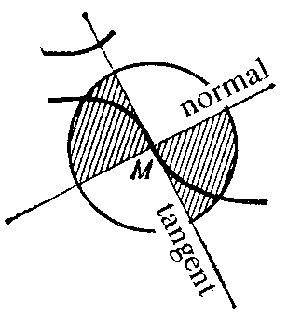
Figure: p073190a
Let a function $ f $ be defined in a certain neighbourhood around a point $ x _ {0} $ and let it be continuous at that point. The point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the end of a range of strict convexity upwards and the end of a range of strict convexity downwards. In that case the point $ ( x _ {0} , f( x _ {0} )) $ is called a point of inflection on the graph of the function, i.e. the graph of $ f $ at $ ( x _ {0} , f( x _ {0} )) $" inflects" through the tangent to it at that point; for $ x < x _ {0} $ the tangent lies under the graph of $ f $, while for $ x > x _ {0} $ it lies above that graph (or vice versa, Fig. b).
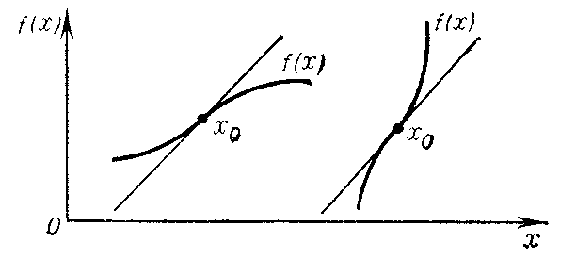
Figure: p073190b
A necessary existence condition for a point of inflection is: If $ f $ is twice differentiable in some neighbourhood of a point $ x _ {0} $, and if $ x _ {0} $ is a point of inflection, then $ f ^ { \prime\prime } ( x _ {0} ) = 0 $. A sufficient existence condition for a point of inflection is: If $ f $ is $ k $ times continuously differentiable in a certain neighbourhood of a point $ x $, with $ k $ odd and $ k \geq 3 $, while $ f ^ { ( n) } ( x _ {0} ) = 0 $ for $ n = 2 \dots k- 1 $, and $ f ^ { ( k) } ( x _ {0} ) \neq 0 $, then $ f $ has a point of inflection at $ x _ {0} $.
References
| [1] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 2 , MIR (1982) (Translated from Russian) |
| [2] | L.D. Kudryavtsev, "A course in mathematical analysis" , 1 , Moscow (1981) (In Russian) |
Comments
References
| [a1] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
| [a2] | J.L. Coolidge, "Algebraic plane curves" , Dover, reprint (1959) |
Point of inflection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Point_of_inflection&oldid=48212