Poincaré return map
successor mapping, of a smooth or at least continuous flow (continuous-time dynamical system) $ S = \{ S _ {t} \} $
and a hypersurface $ V $
transversal to it
A mapping $ T $ that assigns to a point $ v \in V $ that point of the intersection of $ V $ and the positive semi-trajectory of the flow starting at $ v $ that comes first in time (it is defined for those $ v $ for which such an intersection exists). (The hypersurface $ V $ is called a section, an intersecting surface or a transversal.) If the dimension $ \mathop{\rm dim} V = 1 $( so $ \{ S _ {t} \} $ is a flow in the plane or on a two-dimensional surface, $ V $ is called a contactless arc) and if $ V $ is parametrized by a numerical parameter $ s $, then the shift of points of $ V $ under the Poincaré return map is described by some numerical function in one variable (if $ v $ corresponds to the parameter value $ s $, then $ T v $ corresponds to the parameter value $ s + f ( s) $), which is called the successor function. This mapping was used for the first time by H. Poincaré (see ), that is why it is called the Poincaré return map.
If all semi-trajectories intersect $ V $, then the Poincaré return map (in this case defined on the whole of $ V $) determines the behaviour of all trajectories of the flow to a considerable extent. However, such "global" sections are far from being common (in particular, a Hamiltonian system on a manifold of constant energy which does not pass through critical points of the Hamiltonian, i.e. through equilibrium positions (cf. Equilibrium position), does not have closed — as manifolds — global sections, see [3], Chapt. 8, Sect. 4.7).
For a non-autonomous system with a periodic right-hand side,
$$ \tag{* } \dot{x} = f ( t , x ) ,\ f ( t + \tau , x ) = \ f ( t , x ) , $$
there exists an analogue of the Poincaré return map: to the point $ x $ corresponds the point $ T x = \phi ( \tau , x ) $, where $ \phi ( t , x ) $ is the solution of (*) with initial value $ \phi ( 0 , x ) = x $. This "map of the shift by a period" can be considered even formally as a Poincaré return map if (*) is considered as an autonomous system in "cylindrical" phase space. The map $ T $ is defined everywhere if the solutions of (*) are defined for all $ t $.
More often one has to deal with a "local" section — it is cut only by a part of the trajectories and often only part of the trajectories intersecting it return again to $ V $. As an example one can consider a small smooth "surface element" of codimension 1 intersecting transversally some periodic trajectory $ L $. In this case the Poincaré return map is defined near $ V \cap L $ and characterizes the behaviour of the trajectories near $ L $.
In the theory of foliations one can also introduce a Poincaré return map (see [2]), which is a generalization of the above example (and includes the Poincaré return map for ordinary differential equations in a complex domain).
References
| [1a] | H. Poincaré, "Mémoire sur les courbes définiés par une équation differentielle" J. de Math. , 7 (1881) pp. 375–422 Zbl 13.0591.01 |
| [1b] | H. Poincaré, "Mémoire sur les courbes définiés par une équation differentielle" J. de Math. , 8 (1882) pp. 251–296 Zbl 14.0666.01 |
| [1c] | H. Poincaré, "Mémoire sur les courbes définiés par une équation differentielle" J. de Math. , 1 (1885) pp. 167–244 Zbl 14.0666.01 Zbl 13.0591.01 |
| [1d] | H. Poincaré, "Mémoire sur les courbes définiés par une équation differentielle" J. de Math. , 2 (1886) pp. 151–217 Zbl 14.0666.01 Zbl 13.0591.01 |
| [2] | I. Tamura, "Topology of foliations" , Iwanami Shoten (1976) (In Japanese) MR0669379 MR0563523 Zbl 0584.57001 |
| [3] | C. Godbillion, "Géométrie différentielle et mécanique analytique" , Hermann (1969) |
Comments
The return map $ T $ faithfully reflects many properties of the flow $ S $. For example, a point $ p $ which is periodic under $ T $ is necessarily periodic under $ S $, with a possibly different period. Moreover, the $ T $- orbit of $ p $ is asymptotically stable if and only if the $ S $- orbit has the same property. In many ways the discrete-time dynamics of $ T $ are easier to analyze than the continuous-time dynamics of the original flow $ S $. Poincaré exploited these ideas in his study of homoclinic orbits in the three-body problem [a7].
Every diffeomorphism $ g $ of a smooth manifold $ M $ can be identified with a return map: $ M $ is obtained from $ V \times \mathbf R $ by the identifications $ ( x, s) = ( g ( x), s- 1) $; the flow $ S $ on $ M $ is induced by the flow $ \widetilde{S} $ on $ V \times \mathbf R $ given by $ {\widetilde{S} } _ {t} ( x, s) = ( x, s+ t) $; then $ V \times 0 $ is a global section with return map $ g $. By this construction many results proved for flows can be applied to diffeomorphisms.
For the case when all semi-trajectories intersect $ V $ see [a8].
The "cylindrical" phase space mentioned above is defined as follows. Consider the autonomous system associated with (*), i.e.,
$$ \tag{a1 } \dot{x} = f( y, x) ,\ \ \dot{y} = 1 . $$
Identify the point $ ( y, x) $ with $ ( y+ \tau , x) $ for every $ ( y, x) $ in the domain of $ f $; note that the latter is of the form $ \mathbf R \times D $, where $ D $ is a subset of $ \mathbf R ^ {n} $( when (*) is defined in $ \mathbf R ^ {n} $). Then (a1) defines a dynamical system on the "cylinder" $ I _ \tau \times D $, where $ I _ \tau $ is the closed interval $ [ 0, \tau ] $ with the end-points identified, i.e., $ I _ \tau $ is a circle. The mapping $ T : x \mapsto \phi ( \tau , x) $ considered above now coincides with the Poincaré map of the system (a1) on $ I _ \tau \times D $ in the hypersurface $ \{ 0 \} \times D $.
For the existence of global sections, see e.g. [a2], Sect. IV.2, and [a3]. In the context of more general transformation groups one speaks of "global sliceglobal slices" ; see e.g. [a1]. As to the existence of local sections in non-differentiable dynamical systems, see [a4], Sect. VI.2. In the theory of foliations one can recover the generalization of the Poincaré return map in the generators of the (leaf) holonomy groups. See e.g. [a6].
For applications of the Poincaré return map in the theory of differential equations (behaviour near a periodic orbit), see e.g. [a5] (so-called "Floquet theoryFloquet theory" ).
References
| [a1] | H. Abels, "Parallelizability of proper actions, global 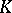 -slices and maximal compact subgroups" Math. Ann. , 212 (1974) pp. 1–19 -slices and maximal compact subgroups" Math. Ann. , 212 (1974) pp. 1–19 |
| [a2] | N.P. Bhatia, G.P. Szegö, "Stability theory of dynamical systems" , Springer (1970) MR0289890 Zbl 0213.10904 |
| [a3] | O. Hajek, "Parallelizability revisited" Proc. Amer. Math. Soc. , 27 (1971) pp. 77–84 |
| [a4] | O. Hajek, "Dynamical systems in the plane" , Acad. Press (1968) MR0240418 Zbl 0169.54401 |
| [a5] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) MR0658490 Zbl 0476.34002 |
| [a6] | G. Hector, U. Hirsch, "Introduction to the geometry of foliations" , Vieweg (1981) MR0639738 Zbl 0486.57002 |
| [a7] | H. Poincaré, "Les méthodes nouvelles de la mécanique céleste" , I , Gauthier-Villars (1899) MR0926908 MR0926907 MR0926906 MR0087814 MR0087813 MR0087812 Zbl 30.0834.08 |
| [a8] | D. Fried, "The geometry of cross-sections to flows" Topology , 21 (1982) pp. 353–371 |
Poincaré return map. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poincar%C3%A9_return_map&oldid=48206