Parabolic-equation method
A method for the approximate solution of a high-frequency diffraction problem (see Diffraction, mathematical theory of). As a rule it is necessary to resort to the parabolic-equation method for the determination of a wave field in those domains where the ray method cannot be employed because the field of rays suffers from a singularity in one sense or another. Consider, for example, the incidence of a plane wave on a perfectly reflecting convex body. The wave phenomenon is described by the Helmholtz equation
$$ \tag{1 } \left ( \frac{\partial ^ {2} }{\partial x ^ {2} } + \frac{\partial ^ {2} }{ \partial y ^ {2} } + k ^ {2} \right ) u = 0. $$
Here the point $ ( x, y) $ is located outside the bounded convex domain $ \Omega $, on the boundary of which the Dirichlet boundary condition $ u \mid _ {S} = 0 $ is satisfied. It is assumed that $ \partial \Omega = S \in C ^ \infty $ has everywhere positive curvature. The solution $ u $ can be represented as $ e ^ {ikx} + u ^ {0} $, where $ u ^ {0} $ satisfies the radiation conditions. The solution of such a problem exists and is unique.
In the high-frequency range ( $ k $" large" ) it is important to construct a formal small wavelength solution to this problem (i.e. roughly speaking, an expansion that formally satisfies all the conditions of the problem, while successive terms are of increasingly high order of smallness as $ k \rightarrow \infty $). It is possible to show that, in the case under consideration, a formal solution will be an asymptotic expansion of the classical solution.
The ray method allows one to construct the unknown small wavelength expansion everywhere, except in the shadow zone (see Fig.). Rays of the incident wave shadow penumbra region
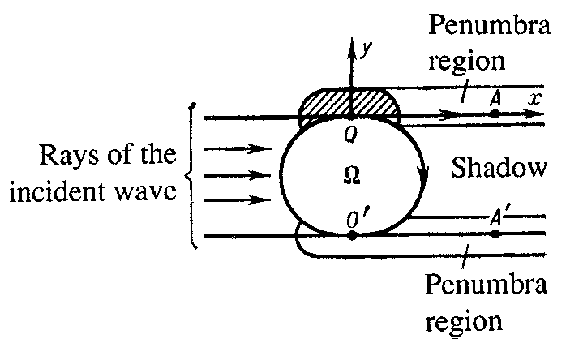
Figure: p071200a
The expression for the wave field constructed with the aid of the ray method loses smoothness on the boundary between shadow zone and illuminated zone (the half-lines $ OA $ and $ O ^ \prime A ^ \prime $ in the figure). In a neighbourhood of $ OA $( and $ O ^ \prime A ^ \prime $) the small wavelength asymptotic expansion of the wavefield is no longer given by the ray formulas. A neighbourhood of $ OA $( and $ O ^ \prime A ^ \prime $) is usually called a penumbra region.
Of key importance for the construction of a formal solution to the problem given above is an examination of the points $ O $ and $ O ^ \prime $ where the rays of the incident wave are the boundary curve $ S = \partial \Omega $. The point $ O $ is taken as the origin of coordinates, and the positive $ x $- axis separates the shadow zone and the illuminated zone.
One introduces new coordinates $ s $ and $ n $ in a neighbourhood of $ O $. A point $ M \notin S $ is determined by its distance along $ S $ from $ O $. It is assumed that $ s > 0 $( respectively, $ s < 0 $) in the shadow zone (respectively, in the illuminated zone). If $ M \in \Omega $, the point $ M $ is characterized by its distance $ n $ from $ S $ and the coordinates $ s $ of the projection of $ M $ on $ S $. With respect to the coordinates $ s $ and $ n $, the Helmholtz equation takes the form
$$ \tag{2 } \left ( 1 + \frac{n} \rho \right ) ^ {-} 1 \left [ \frac \partial {\partial n } \left ( \left ( 1 + \frac{n} \rho \right ) \frac{\partial u }{\partial n } \right ) \right . + $$
$$ + \left . \frac \partial {\partial s } \left ( \left ( 1 + \frac{n} \rho \right ) ^ {-} 1 \frac{\partial u }{\partial s } \right ) \right ] + k ^ {2} u = 0 $$
( $ \rho = \rho ( s) > 0 $ is the radius of curvature of $ S $ at the point $ s $). Through the MacLaurin series for $ 1/ \rho $,
$$ \frac{1} \rho \sim \left . \frac{1} \rho \right | _ {s=} 0 + s \left ( \frac{d}{ds} \left ( \frac{1} \rho \right ) \right ) _ {s=} 0 + \dots , $$
it is possible to replace all the coefficients of equation (2) by their formal expansions in powers of $ s $ and $ n $. Substituting the coordinates
$$ \sigma = \frac{k ^ {1/3} s }{2 ^ {1/3} \rho ^ {2/3} } ,\ \ \nu = \left ( \frac{2}{\rho _ {0} } \right ) ^ {1/3} k ^ {2/3} n,\ \ \rho _ {0} = \rho ( 0), $$
in equations (2), one arrives at
$$ \tag{3 } u \sim e ^ {iks} ( v _ {0} ( \sigma , \nu ) + k ^ {-} 1/3 v _ {1} ( \sigma ,\ \nu ) + \dots ) . $$
By equating to zero the coefficients of the successive powers of $ k ^ {-} 1/3 $, one obtains the following sequence of recurrence relations (which is typical for the method of boundary layers, cf. also Boundary-layer theory):
$$ L _ {0} v _ {0} = 0,\ \ L _ {0} v _ {1} + L _ {1} v _ {0} = 0,\ \ L _ {0} v _ {2} + L _ {1} v _ {1} + L _ {2} v _ {0} = 0. $$
Here the first equation is a "parabolic" equation, leading to the name parabolic-equation method:
$$ \tag{4 } L _ {0} v _ {0} \equiv i \frac{\partial v _ {0} }{\partial \sigma } + \frac{\partial ^ {2} v _ {0} }{\partial \nu ^ {2} } + \nu v _ {0} = 0. $$
Basically, equation (4) is an equation of Schrödinger type. The coefficients in the operator $ L _ {j} $ are polynomials in $ \sigma $ and $ \nu $. For the formal satisfaction of the boundary condition $ u \mid _ {S} = 0 $ it is sufficient to require that $ u _ {j} \mid _ {S} = 0 $. The other boundary conditions require that for large $ | \sigma | $, $ \sigma < 0 $, the sequence (3) formally becomes the expansion of the ray method. For $ v _ {0} $ it is possible to derive an explicit formula (the so-called Fock formula), having the form of a Fourier integral:
$$ \int\limits e ^ {i \sigma \zeta } \Phi ( \nu , \zeta ) d \zeta , $$
where $ \Phi $ is expressed comparatively simply in terms of Airy functions. Methods of matching asymptotics enable one to obtain formulas for the wave field in all shadow and penumbra regions.
In the case of creeping waves and of whispering gallery modes, corresponding "parabolic" equations have been deduced and their solutions are expressed in terms of Airy functions. The development of the theory of lasers made it necessary to consider waves concentrated in a neighbourhood of isolated rays. Selecting the corresponding phase coefficient and carrying out further constructions analogous to the constructions of the boundary-layer method, a "parabolic" equation is obtained, in terms of the solution of which the wave field is expressed in a first approximation. In this case the "parabolic" equation will be the Schrödinger equation with a quadratic potential. The parabolic-equation method finds application also in the calculation of the wave field in shallow water, in statistical non-homogeneous media and in many other problems. Analogues of the parabolic-equation method are used in the theory of non-linear waves.
References
| [1] | V.A. [V.A. Fok] Fock, "Electromagnetic diffraction and propagation problems" , Pergamon (1965) (Translated from Russian) |
| [2] | V.M. Babich, V.S. Buldyrev, "Asymptotic methods in the diffraction of short waves" , Moscow (1972) (In Russian) (Translation forthcoming: Springer) |
| [3] | V.M. [V.M. Babich] Babič, N.Y. [N.Ya. Kirpichnikova] Kirpičnikova, "The boundary-layer method in diffraction problems" , Springer (1979) (Translated from Russian) |
Comments
References
| [a1] | N. Maruvitz, "Radiation and scattering of waves" , Prentice-Hall (1973) |
Parabolic-equation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parabolic-equation_method&oldid=48104