P-divisible group
Barsotti–Tate group
A generalization of the concept of a commutative formal group of finite height. The homomorphism induced by multiplication by the prime number 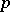 is an epimorphism for a
is an epimorphism for a 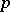 -divisible group.
-divisible group.
Let 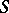 be a scheme and let
be a scheme and let  be a prime number. A
be a prime number. A 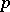 -divisible group of height
-divisible group of height  is an inductive system
is an inductive system 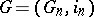 of commutative finite group schemes
of commutative finite group schemes 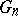 of order
of order 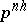 (cf. Group scheme) such that the sequences
(cf. Group scheme) such that the sequences
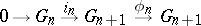 |
are exact (cf. Exact sequence; here  is the homomorphism of multiplication by
is the homomorphism of multiplication by 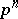 ). A morphism of
). A morphism of  -divisible groups is a morphism of the inductive systems. A
-divisible groups is a morphism of the inductive systems. A  -divisible group is said to be connected (respectively, étale) if all
-divisible group is said to be connected (respectively, étale) if all  are connected (respectively, étale) group schemes. A connected
are connected (respectively, étale) group schemes. A connected 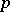 -divisible group over a field of characteristic
-divisible group over a field of characteristic 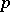 is a commutative formal group (considered as the inductive limit of the kernels of
is a commutative formal group (considered as the inductive limit of the kernels of 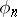 , i.e. of multiplication by
, i.e. of multiplication by 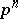 ) for which multiplication by
) for which multiplication by 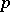 is an isogeny [6]. This fact is generalized to include the case of an arbitrary base scheme
is an isogeny [6]. This fact is generalized to include the case of an arbitrary base scheme  on which the homomorphism induced by multiplication by
on which the homomorphism induced by multiplication by 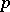 is locally nilpotent [4]. The category of étale
is locally nilpotent [4]. The category of étale 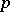 -divisible groups is equivalent to the category of
-divisible groups is equivalent to the category of 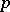 -adic representations of the fundamental group of the scheme
-adic representations of the fundamental group of the scheme  . Each
. Each 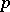 -divisible group
-divisible group 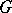 over an Artinian scheme
over an Artinian scheme 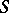 contains a maximal connected subgroup
contains a maximal connected subgroup 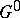 , which is known as the connected component of the identity, the quotient by which is an étale
, which is known as the connected component of the identity, the quotient by which is an étale 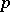 -divisible group. The dimension of the Lie algebra of any
-divisible group. The dimension of the Lie algebra of any 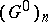 is said to be the dimension of the
is said to be the dimension of the 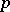 -divisible group
-divisible group  .
.
Let 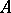 be an Abelian variety over the field
be an Abelian variety over the field  of dimension
of dimension 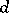 , let
, let  be the kernel of the homomorphism of multiplication by
be the kernel of the homomorphism of multiplication by 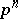 in
in  and let
and let 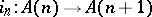 be a natural inclusion. The inductive system
be a natural inclusion. The inductive system  is a
is a 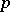 -divisible group of height
-divisible group of height 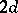 . Its connected component of the identity
. Its connected component of the identity  coincides with the formal completion of
coincides with the formal completion of  along the unit section, while the height of
along the unit section, while the height of  equals
equals 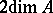 .
.
Let 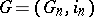 be a
be a  -divisible group of height
-divisible group of height  , let
, let 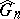 denote the Cartier dual finite group schemes and let
denote the Cartier dual finite group schemes and let 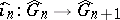 be the mapping dual to the mapping of multiplication by
be the mapping dual to the mapping of multiplication by 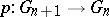 . The system
. The system 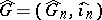 is then a
is then a 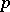 -divisible group of height
-divisible group of height 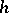 and is called the Serre dual to the
and is called the Serre dual to the 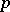 -divisible group
-divisible group  . The sum of the dimensions of
. The sum of the dimensions of 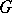 and
and 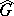 is equal to
is equal to  .
.
As in formal groups, so, too, in  -divisible groups, the concept of a Dieudonné module, which plays an important role in the deformation theory of
-divisible groups, the concept of a Dieudonné module, which plays an important role in the deformation theory of 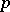 -divisible groups [2], [3], [4] may be introduced.
-divisible groups [2], [3], [4] may be introduced.
If 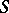 is the spectrum of an unequal-characteristic discrete valuation ring
is the spectrum of an unequal-characteristic discrete valuation ring 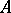 with residue field of characteristic
with residue field of characteristic 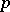 , the structure of a
, the structure of a 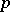 -divisible group is closely connected with the structure of the completion of the algebraic closure of the quotient field
-divisible group is closely connected with the structure of the completion of the algebraic closure of the quotient field 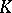 of
of 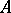 , considered as a module over the Galois group of the field
, considered as a module over the Galois group of the field  [6].
[6].
References
| [1] | I. Barsotti, "Analytic methods for abelian varieties in positive characteristic" , Coll. Théorie des Groupes Algébriques (Bruxelles, 1962) , Gauthier-Villars (1962) pp. 77–85 |
| [2] | A. Grothendieck, "Groupes de Barsotti–Tate et cristaux" , Proc. Internat. Congress Mathematicians (Nice, 1970) , 1 , Gauthier-Villars (1971) pp. 431–436 |
| [3] | B. Mazur, W. Messing, "Universal extensions and one-dimensional crystalline cohomology" , Springer (1974) |
| [4] | W. Messing, "The crystals associated to Barsotti–Tate groups: with applications to Abelian schemes" , Springer (1972) |
| [5] | J.-P. Serre, "Groupes 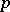 -divisibles (d'après J. Tate)" , Sem. Bourbaki , 318 , Benjamin (1968) -divisibles (d'après J. Tate)" , Sem. Bourbaki , 318 , Benjamin (1968) |
| [6] | J.T. Tate, "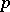 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 |
Comments
References
| [a1] | M. Demazure, "Lectures on 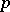 -divisible groups" , Lect. notes in math. , 302 , Springer (1972) -divisible groups" , Lect. notes in math. , 302 , Springer (1972) |
P-divisible group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=P-divisible_group&oldid=13472