Operator vessel
The theory of operator vessels provides a framework for the spectral analysis and synthesis of tuples of commuting non-self-adjoint (or non-unitary) operators, especially for operators that are not "too far" from being self-adjoint (or unitary). It reveals deep connections with algebraic geometry, especially with function theory on a compact real Riemann surface (i.e., a compact Riemann surface endowed with an anti-holomorphic involution, cf. also Riemann surface), and with the theory of multi-dimensional systems. The theory of operator vessels can be also generalized for the study of tuples of non-commuting non-self-adjoint (or non-unitary) operators (cf. also Non-self-adjoint operator), especially for non-self-adjoint representations of Lie algebras (or non-unitary representations of discrete groups).
Let $A _ { 1 }$, $A _ { 2 }$ be a pair of commuting bounded linear operators in a Hilbert space $\mathcal{H}$. A quasi-Hermitian commutative two-operator vessel $\frak V$ is a collection
\begin{equation} \tag{a1} \mathfrak { V } = ( A _ { 1 } , A _ { 2 } , \mathcal H , \Phi , \mathcal E , \sigma _ { 1 } , \sigma _ { 2 } , \gamma , \widetilde { \gamma } ). \end{equation}
Here, $\cal E$ is an auxiliary Hilbert space called the external space of the vessel ($\mathcal{H}$ is called the internal space), $\Phi : \mathcal{H} \rightarrow \mathcal{E}$ is a bounded linear mapping, $\sigma _ { 1 }$, $\sigma 2$, $\gamma$, $\tilde{\gamma}$ are bounded self-adjoint operators in $\cal E$ (cf. also Self-adjoint operator), such that
\begin{equation} \tag{a2} \frac { 1 } { i } ( A _ { 1 } - A _ { 1 } ^ { * } ) = \Phi ^ { * } \sigma _ { 1 } \Phi , \frac { 1 } { i } ( A _ { 2 } - A _ { 2 } ^ { * } ) = \Phi ^ { * } \sigma _ { 2 } \Phi, \end{equation}
\begin{equation} \tag{a3} \sigma _ { 1 } \Phi A _ { 2 } ^ { * } - \sigma _ { 2 } \Phi A _ { 1 } ^ { * } = \gamma \Phi , \end{equation}
\begin{equation} \tag{a4} \sigma _ { 1 } \Phi A _ { 2 } - \sigma _ { 2 } \Phi A _ { 1 } = \widetilde { \gamma } \Phi, \end{equation}
\begin{equation} \tag{a5} \tilde { \gamma } - \gamma = i ( \sigma _ { 1 } \Phi \Phi ^ { * } \sigma _ { 2 } - \sigma _ { 2 } \Phi \Phi ^ { * } \sigma _ { 1 } ). \end{equation}
The equations (a2) are so-called colligation conditions (or node conditions) well-known from the spectral analysis of a single non-self-adjoint operator (cf. also Operator colligation); they allow one to "isolate" the non-Hermitian parts of the operators $A _ { 1 }$ and $A _ { 2 }$. The equations (a3), (a4) and (a5) are deeper; the self-adjoint operators $\gamma$ and $\tilde{\gamma}$ carry information about the interaction of $A _ { 1 }$ and $A _ { 2 }$.
Notice that a given pair $A _ { 1 }$, $A _ { 2 }$ of commuting operators in $\mathcal{H}$ can be always embedded in a quasi-Hermitian commutative vessel by setting
\begin{equation*} \mathcal{E} = \overline { ( A _ { 1 } - A _ { 1 } ^ { * } ) \mathcal{H} + ( A _ { 2 } - A _ { 2 } ^ { * } ) \mathcal{H} , } \Phi = P _ { \mathcal{E} }, \end{equation*}
\begin{equation*} \sigma _ { 1 } = \frac { 1 } { i } ( A _ { 1 } - A _ { 1 } ^ { * } ) | _ {\cal E } , \sigma _ { 2 } = \frac { 1 } { i } ( A _ { 2 } - A _ { 2 } ^ { * } ) | _ { \cal E } , \gamma = \frac { 1 } { i } ( A _ { 1 } A _ { 2 } ^ { * } - A _ { 2 } A _ { 1 } ^ { * } ) | _ { \cal E } , \widetilde { \gamma } = \frac { 1 } { i } ( A _ { 2 } ^ { * } A _ { 1 } - A _ { 1 } ^ { * } A _ { 2 } ) | _ { \cal E } \end{equation*}
($P _ { \mathcal{E}}$ denotes the orthogonal projection on the subspace $\cal E$; it is an easy consequence of the commutativity of $A _ { 1 }$ and $A _ { 2 }$ that $\cal E$ is invariant under $A _ { 1 } A _ { 2 } ^ { * } - A _ { 2 } A _ { 1 } ^ { * }$ and $A _ { 2 } ^ { * } A _ { 1 } - A _ { 1 } ^ { * } A _ { 2 }$).
The notion of an operator vessel allows one to construct commuting operators with more complicated spectral data out of commuting operators with simpler spectral data while controlling the non-Hermitian parts. Let
\begin{equation*} \mathfrak { V } ^ { \prime } = ( A _ { 1 } ^ { \prime } , A _ { 2 } ^ { \prime } , \mathcal{H} ^ { \prime } , \Phi ^ { \prime } , \mathcal{E} , \sigma _ { 1 } , \sigma _ { 2 } , \gamma ^ { \prime } , \widetilde { \gamma } ^ { \prime } ), \end{equation*}
\begin{equation*} \mathfrak { V } ^ { \prime \prime } = ( A _ { 1 } ^ { \prime \prime } , A _ { 2 } ^ { \prime \prime } , \mathcal{H} ^ { \prime \prime } , \Phi ^ { \prime \prime } , \mathcal{E} , \sigma _ { 1 } , \sigma _ { 2 } , \gamma ^ { \prime \prime } , \widetilde { \gamma } ^ { \prime \prime } ) \end{equation*}
be two quasi-Hermitian commutative vessels with the same $( \mathcal{E} , \sigma _ { 1 } , \sigma _ { 2 } )$. Using the coupling construction familiar in the spectral analysis of a single non-self-adjoint operator, one sets $\mathcal{H} = \mathcal{H} ^ { \prime } \oplus \mathcal{H} ^ { \prime \prime }$ and defines operators $A _ { 1 } , A _ { 2 } : \mathcal{H} \rightarrow \mathcal{H}$ and $\Phi : \mathcal{H} \rightarrow \mathcal{E}$ by
\begin{equation} \tag{a6} A _ { k } = \left( \begin{array} { c c } { A _ { k } ^ { \prime } } & { 0 } \\ { i \Phi ^ { \prime \prime } \sigma _ { k } \Phi ^ { \prime } } & { A _ { k } ^ { \prime \prime } } \end{array} \right) ( k = 1,2 ), \end{equation}
\begin{equation*} \Phi = ( \Phi ^ { \prime } \Phi ^ { \prime \prime } ) \end{equation*}
(the operators being written in block form with respect to the direct sum decomposition $\mathcal{H} = \mathcal{H} ^ { \prime } \oplus \mathcal{H} ^ { \prime \prime }$). It is clear that $A _ { 1 }$, $A _ { 2 }$ satisfy the colligation conditions:
\begin{equation*} \frac { 1 } { i } ( A _ { k } - A _ { k } ^ { * } ) = \Phi ^ { * } \sigma _ { k } \Phi , \end{equation*}
but in general they do not commute. It turns out that $A _ { 1 } A _ { 2 } = A _ { 2 } A _ { 1 }$ exactly when $\tilde { \gamma } ^ { \prime } = \gamma ^ { \prime \prime }$; more precisely,
\begin{equation*} \mathfrak { V } = ( A _ { 1 } , A _ { 2 } , \mathcal{H} , \Phi , \mathcal{E} , \sigma _ { 1 } , \sigma _ { 2 } , \gamma , \widetilde { \gamma } ) \end{equation*}
(with $\gamma = \gamma ^ { \prime }$ and $\tilde { \gamma } = \tilde { \gamma } ^ { \prime \prime }$) is a quasi-Hermitian commutative vessel if and only if $\tilde { \gamma } ^ { \prime } = \gamma ^ { \prime \prime }$ (the matching theorem).
Assume now that the external space $\cal E$ of a vessel $\frak V$ as in (a1) is finite dimensional; one defines a polynomial in two complex variables $\lambda _ { 1 }$, $\lambda _ { 2 }$ by setting
\begin{equation} \tag{a7} p ( \lambda _ { 1 } , \lambda _ { 2 } ) = \operatorname { det } ( \lambda _ { 1 } \sigma _ { 2 } - \lambda _ { 2 } \sigma _ { 1 } + \gamma ). \end{equation}
It is assumed that $\operatorname { det } ( \xi _ { 1 } \sigma _ { 1 } + \xi _ { 2 } \sigma _ { 2 } ) \not \equiv 0$, so that $p ( \lambda _ { 1 } , \lambda _ { 2 } ) \not\equiv 0$ and $p ( \lambda _ { 1 } , \lambda _ { 2 } )$ is a polynomial with real coefficients of degree $M = \operatorname { dim } \mathcal{E}$. One calls $p ( \lambda _ { 1 } , \lambda _ { 2 } )$ the discriminant polynomial of the vessel $\frak V$, and the projective plane real algebraic curve with an affine equation $p ( \lambda _ { 1 } , \lambda _ { 2 } ) = 0$ — the discriminant curve. A generalized Cayley–Hamilton theorem holds: $p ( A _ { 1 } , A _ { 2 } ) = 0$ (under the natural minimality assumption $H = \vee_{ k _ { 1 } , k _ { 2 } = 0}^\infty A _ { 1 } ^ { k _ { 1 } } A _ { 2 } ^ { k _ { 2 } } \Phi ^ { * } {\cal E}$). It follows that the joint spectrum of $A _ { 1 }$, $A _ { 2 }$ (cf. also Taylor joint spectrum) lies on the (affine part of the) discriminant curve.
The following remarkable equality also holds:
\begin{equation} \tag{a8} \operatorname { det } ( \lambda _ { 1 } \sigma _ { 2 } - \lambda _ { 2 } \sigma _ { 1 } + \gamma ) = \operatorname { det } ( \lambda _ { 1 } \sigma _ { 2 } - \lambda _ { 2 } \sigma _ { 1 } + \widetilde { \gamma } ). \end{equation}
Thus, associated to the vessel $\frak V$ there is the discriminant polynomial $p ( \lambda _ { 1 } , \lambda _ { 2 } )$, and two self-adjoint determinantal representations of it, $\lambda _ { 1 } \sigma _ { 2 } - \lambda _ { 2 } \sigma _ { 1 } + \gamma$ and $\lambda _ { 1 } \sigma _ { 2 } - \lambda _ { 2 } \sigma _ { 1 } + \tilde { \gamma }$, called (for system-theoretic reasons, see below) the input and the output determinantal representations, respectively.
Consider now the inverse problem of constructing, up to unitary equivalence, all (minimal) quasi-Hermitian commutative two-operator vessels with given discriminant polynomial $p ( \lambda _ { 1 } , \lambda _ { 2 } )$, given input determinantal representations $\lambda _ { 1 } \sigma _ { 2 } - \lambda _ { 2 } \sigma _ { 1 } + \gamma$, and with the operators $A _ { 1 }$, $A _ { 2 }$ in the vessel having given joint spectrum $\frak S$, which is a subset of the affine part of the real projective plane curve $C$ defined by $p ( \lambda _ { 1 } , \lambda _ { 2 } )$. Here, two vessels $\mathfrak { V } ^ { ( l ) } = ( A _ { 1 } ^ { ( l ) } , A _ { 2 } ^ { ( l ) } , \mathcal{H} ^ { ( l ) } , \Phi ^ { ( l ) } , \mathcal{E} , \sigma _ { 1 } , \sigma _ { 2 } , \gamma , \tilde { \gamma } )$ ($l = 1,2$) are said to be unitarily equivalent if there is an isometric mapping $U$ from $\mathcal{H}^{ ( 1 )}$ onto $\mathcal{H}^{ ( 2 )}$ such that
\begin{equation} \tag{a9} A _ { k } ^ { ( 2 ) } = U A _ { k } ^ { ( 1 ) } U ^ { - 1 } ( k = 1,2 ), \end{equation}
\begin{equation*} \Phi ^ { ( 2 ) } = \Phi ^ { ( 1 ) } U. \end{equation*}
If $p ( \lambda _ { 1 } , \lambda _ { 2 } )$ is an irreducible polynomial and $C$ is a smooth irreducible curve (these assumptions can be relaxed), a complete and explicit solution of the inverse problem stated above has been obtained. This solution leads to triangular models for the corresponding pair of operators $A _ { 1 }$, $A _ { 2 }$ with finite non-Hermitian ranks, similar to the well-known triangular models for a single non-self-adjoint operator. The solution is based on first constructing elementary objects — vessels with one-dimensional internal space corresponding to the points of the joint spectrum — and then coupling them using the matching theorem. It follows from (a5) that in a vessel with one-dimensional internal space the output determinantal representation is determined by the input determinantal representation and the spectral data; the successive matching of output and input determinantal representations in the matching theorem then gives a system of non-linear difference (for the discrete part of the spectrum) and differential (for the continuous part of the spectrum) equations for self-adjoint determinantal representations of the polynomial $p ( \lambda _ { 1 } , \lambda _ { 2 } )$. The algebro-geometric assumptions on the polynomial $p ( \lambda _ { 1 } , \lambda _ { 2 } )$ and the curve $C$ imply that self-adjoint determinantal representations are naturally parametrized by certain points in the Jacobi variety of $C$; and it turns out that passing from a self-adjoint determinantal representation to the corresponding point in the Jacobi variety linearizes the systems of non-linear difference and differential equations alluded to above. Actually, the system can even be solved explicitly using theta-functions, yielding explicit formulas for the operators $A _ { 1 }$, $A _ { 2 }$ in a triangular model.
The fundamental interplay between the spectral theory of a pair of commuting non-self-adjoint operators with finite non-Hermitian ranks and function theory on a compact real Riemann surface is based on the notion of the joint characteristic function. Let $\frak V$ be a quasi-Hermitian commutative vessel as in (a1), with discriminant polynomial $p ( \lambda _ { 1 } , \lambda _ { 2 } )$ and discriminant curve $C$. For each affine point $\lambda = ( \lambda _ { 1 } , \lambda _ { 2 } )$ on $C$, one may define two non-trivial subspaces of the external space $\cal E$:
\begin{equation} \tag{a10} \mathfrak { E } ( \lambda ) = \operatorname { ker } ( \lambda _ { 1 } \sigma _ { 2 } - \lambda _ { 2 } \sigma _ { 1 } + \gamma ), \end{equation}
\begin{equation} \tag{a11} \tilde{\mathfrak{E}} ( \lambda ) = \operatorname { ker } ( \lambda _ { 1 } \sigma _ { 2 } - \lambda _ { 2 } \sigma _ { 1 } + \tilde { \gamma } ). \end{equation}
Then for arbitrary complex numbers $\xi _ { 1 }$, $\xi_2$ (such that $\xi _ { 1 } \lambda _ { 1 } + \xi _ { 2 } \lambda _ { 2 }$ is outside the spectrum of $\xi _ { 1 } A _ { 1 } + \xi _ { 2 } A _ { 2 }$), the operator on $\cal E$,
\begin{equation*} l _ { \mathcal{E} } - i \Phi ( \xi _ { 1 } A _ { 1 } + \xi _ { 2 } A _ { 2 } - \xi _ { 1 } \lambda _ { 1 } - \xi _ { 2 } \lambda _ { 2 } ) ^ { - 1 } \Phi ^ { * } ( \xi _ { 1 } \sigma _ { 1 } + \xi _ { 2 } \sigma _ { 2 } ), \end{equation*}
maps $\mathfrak{E} ( \lambda )$ into $\tilde { \mathfrak{E} } ( \lambda )$ and the restriction of this operator to $\mathfrak{E} ( \lambda )$ is independent of $\xi _ { 1 }$, $\xi_2$. The joint characteristic function of the vessel $\frak V$ is defined by
\begin{equation} \tag{a12} S ( \lambda ) = I _ { \mathcal{E} } - i \Phi ( \xi _ { 1 } A _ { 1 } + \xi _ { 2 } A _ { 2 } - \xi _ { 1 } \lambda _ { 1 } - \xi _ { 2 } \lambda _ { 2 } ) ^ { - 1 }. \end{equation}
\begin{equation*} \Phi ^ { * } ( \xi _ { 1 } \sigma _ { 1 } + \xi _ { 2 } \sigma _ { 2 } ) | _ { \mathfrak { E } ( \lambda ) } : \mathfrak { E } ( \lambda ) \rightarrow \tilde { \mathfrak { E } } ( \lambda ), \end{equation*}
where $\lambda = ( \lambda _ { 1 } , \lambda _ { 2 } )$ is an affine point on $C$ outside the joint spectrum of $A _ { 1 }$, $A _ { 2 }$.
The joint characteristic function is thus a mapping of certain sheaves on the discriminant curve (cf. also Sheaf). For simplicity, assume that the discriminant polynomial $p ( \lambda _ { 1 } , \lambda _ { 2 } )$ has only one, possibly multiple, irreducible factor; thus $p ( \lambda _ { 1 } , \lambda _ { 2 } ) = ( f ( \lambda _ { 1 } , \lambda _ { 2 } ) ) ^ { r }$ for some $r \geq 1$, where $f ( \lambda _ { 1 } , \lambda _ { 2 } ) = 0$ is the irreducible affine equation of the discriminant curve $C$. Assume also that both the input and the output determinantal representations of $p ( \lambda _ { 1 } , \lambda _ { 2 } )$ are maximal, meaning that for every point $\mu$ on $C$ the subspaces $\mathfrak{E} ( \mu )$ and $\tilde { \mathfrak{E} } ( \mu )$ have maximal possible dimension (which is equal to $r$ times the multiplicity of $\mu$ on $C$; notice that all these assumptions are trivially satisfied when the discriminant polynomial is irreducible, i.e., $r = 1$, and $C$ is a smooth irreducible curve). It follows then that the subspaces $\mathfrak{E} ( \mu )$ and $\tilde { \mathfrak{E} } ( \mu )$ for different points $\mu$ on $C$ (including, of course, the points at infinity) fit together to form two complex holomorphic rank-$r$ vector bundles $\mathfrak{C}$ and $\tilde{\frak E}$ on a compact Riemann surface $X$ which is the desingularization of $C$ (cf. also Resolution of singularities). The joint characteristic function $S : \mathfrak { E } \rightarrow \tilde { \mathfrak { C } }$ (naturally extended to be identity at the points of $C$ at infinity) is simply a bundle mapping, holomorphic outside the joint spectrum of $A _ { 1 }$, $A _ { 2 }$. Notice that since $C$ is a real curve, $X$ is a real Riemann surface, that is, a Riemann surface equipped with an anti-holomorphic involution (the complex conjugation on $C$).
Assuming the maximality of the input and the output determinantal representations, the joint characteristic function of a (minimal) vessel determines the vessel uniquely up to unitary equivalence. The joint characteristic function is expansive with respect to certain naturally defined scalar products on the vector bundles $\mathfrak{C}$ and $\tilde{\frak E}$. Conversely, given any bundle mapping between the kernel vector bundles corresponding to the given two maximal self-adjoint determinantal representations, which is expansive with respect to the corresponding scalar products, this bundle mapping can be realized as the joint characteristic function of a quasi-Hermitian commutative vessel with these input and output determinantal representations.
Kernel vector bundles corresponding to maximal self-adjoint determinantal representations are isomorphic (up to an inessential twist) to vector bundles of multiplicative half-order differentials, i.e., to vector bundles of the form $V _ { \chi } \otimes \Delta$; here $\Delta \otimes \Delta \cong K _ { X }$, the canonical line bundle (the line bundle of holomorphic differentials), and $V _ { \mathcal{X} }$ is a flat vector bundle associated to some representation 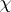 of the fundamental group of $X$. Using this isomorphism one may replace the joint characteristic function by the so-called normalized joint characteristic function, which is simply a mapping of flat vector bundles on $X$, i.e., a multiplicative multi-valued matrix function on $X$ (with appropriate matrix multipliers on the left and on the right). The normalized joint characteristic function is usually more convenient for analytic investigations. There are also functional models for the corresponding pair of operators $A _ { 1 }$, $A _ { 2 }$ with finite non-Hermitian ranks, similar to the well-known functional models of Sz.-Nagy–Foias and de Branges–Rovnyak for a single operator; the model space is an appropriately defined space of multiplicative half-order differentials on $X$, and the model operators are certain "compressed multiplication operators" by the affine coordinate functions $\lambda _ { 1 }$, $\lambda _ { 2 }$.
of the fundamental group of $X$. Using this isomorphism one may replace the joint characteristic function by the so-called normalized joint characteristic function, which is simply a mapping of flat vector bundles on $X$, i.e., a multiplicative multi-valued matrix function on $X$ (with appropriate matrix multipliers on the left and on the right). The normalized joint characteristic function is usually more convenient for analytic investigations. There are also functional models for the corresponding pair of operators $A _ { 1 }$, $A _ { 2 }$ with finite non-Hermitian ranks, similar to the well-known functional models of Sz.-Nagy–Foias and de Branges–Rovnyak for a single operator; the model space is an appropriately defined space of multiplicative half-order differentials on $X$, and the model operators are certain "compressed multiplication operators" by the affine coordinate functions $\lambda _ { 1 }$, $\lambda _ { 2 }$.
Like the notion of colligation in the spectral theory of a single non-self-adjoint operator (cf. also Operator colligation), the notion of a vessel has a system-theoretic significance. Given a quasi-Hermitian commutative two-operator vessel $\frak V$ as in (a1), one writes a linear shift-invariant continuous two-dimensional system
\begin{equation} \tag{a13} i \frac { \partial f } { \partial t _ { 1 } } + A _ { 1 } f = \Phi ^ { * } \sigma _ { 1 } u, \end{equation}
\begin{equation} \tag{a14} i \frac { \partial f } { \partial t _ { 2 } } + A _ { 2 } f = \Phi ^ { * } \sigma _ { 2 } u, \end{equation}
\begin{equation} \tag{a15} v = u - i \Phi f. \end{equation}
Here, $f = f ( t _ { 1 } , t _ { 2 } )$ is the state with values in the internal space $\mathcal{H}$, $u = u ( t _ { 1 } , t _ { 2 } )$ and $v = v ( t _ { 1 } , t _ { 2 } )$ are, respectively, the input and the output with values in the external space $\cal E$, and $( t _ { 1 } , t _ { 2 } ) \in \mathbf{R}^ { 2 }$. The colligation conditions (a2) imply that the system (a13)–(a15) satisfies the energy balance law:
\begin{equation} \tag{a16} \left( \xi _ { 1 } \frac { \partial } { \partial t _ { 1 } } + \xi _ { 2 } \frac { \partial } { \partial t _ { 2 } } \right) \langle f , f \rangle _ { \mathcal{H} } = \end{equation}
\begin{equation*} = \langle ( \xi _ { 1 } \sigma _ { 1 } + \xi _ { 2 } \sigma _ { 2 } ) u , u \rangle _ { \mathcal{E} } - \langle ( \xi _ { 1 } \sigma _ { 1 } + \xi _ { 2 } \sigma _ { 2 } ) v , v \rangle _ { \mathcal{E} } \end{equation*}
for any direction $( \xi _ { 1 } , \xi _ { 2 } )$ in $\mathbf{R} ^ { 2 }$. Unlike the usual one-dimensional systems, the system (a13)–(a15) is overdetermined (cf. also Overdetermined system), the compatibility conditions arising from the equality of mixed partial derivatives:
\begin{equation*} \frac { \partial ^ { 2 } f } { \partial t _ { 1 } \partial t _ { 2 } } = \frac { \partial ^ { 2 } f } { \partial t _ { 2 } \partial t _ { 1 } }. \end{equation*}
The commutativity $A _ { 1 } A _ { 2 } = A _ { 2 } A _ { 1 }$ means precisely that the system is consistent for an arbitrary initial state $f ( 0,0 )$ and the identically zero input. The vessel condition (a3) implies that a sufficient (and under some assumptions also a necessary) condition for the input signal to be compatible is given by
\begin{equation} \tag{a17} \left( \sigma _ { 2 } \frac { \partial } { \partial t _ { 1 } } - \sigma _ { 1 } \frac { \partial } { \partial t _ { 2 } } + \gamma \right) u = 0. \end{equation}
The vessel conditions (a4), (a5) imply that the corresponding output satisfies
\begin{equation} \tag{a18} \left( \sigma _ { 2 } \frac { \partial } { \partial t _ { 1 } } - \sigma _ { 1 } \frac { \partial } { \partial t _ { 2 } } + \tilde { \gamma } \right) v = 0. \end{equation}
The joint characteristic function of the vessel $\frak V$ is the so-called joint transfer function of the overdetermined system (a13)–(a15) together with the compatibility partial differential equations (a17) and (a18) at the input and at the output, respectively.
The notion of a quasi-Hermitian commutative two-operator vessel is the simplest and the best studied; it can be successfully generalized in various directions, like:
1) Quasi-Hermitian commutative $d$-operator vessels for any $d$, which give a framework for the spectral analysis of $d$-tuples of commuting non-self-adjoint operators (especially with finite non-Hermitian ranks).
2) Quasi-unitary commutative operator vessels, which give a framework for the spectral analysis of tuples of commuting non-unitary operators (especially with finite defects); they are related to discrete conservative multi-dimensional systems (rather than continuous).
3) "Non-metric" commutative operator vessels, which correspond to overdetermined multi-dimensional systems together with compatibility partial differential equations at the input and at the output, but without any energy balance laws.
4) Non-commutative generalizations, in particular (quasi-Hermitian) "Lie algebra" vessels, where one replaces a tuple of commuting operators by a representation of a given Lie algebra $\frak g$. Such vessels provide a framework for the spectral analysis of non-self-adjoint representations of $\frak g$. The associated (conservative) multi-dimensional system evolves on a Lie group $G$ having the Lie algebra $\frak g$.
The theory of operator vessels was initiated by M.S. Livšic [a2], [a3]. The term "vessel" was coined in the book [a1]; earlier papers use the term "regular colligation" . The book [a1] provides a comprehensive treatment of the subject. A shorter survey, containing also the more recent results, is [a4].
References
| [a1] | M.S. Livšic, N. Kravitsky, A.S. Markus, V. Vinnikov, "Theory of commuting nonselfadjoint operators" , Kluwer Acad. Publ. (1995) MR1347918 Zbl 0834.47004 |
| [a2] | M.S. Livšic, "Operator waves in Hilbert space and related partial differential equations" Integral Eq. Oper. Th. , 2 : 1 (1979) pp. 25–47 MR0532737 Zbl 0539.47033 Zbl 0407.35072 |
| [a3] | M.S. Livšic, "A method for constructing triangular canonical models of commuting operators based on connections with algebraic curves" Integral Eq. Oper. Th. , 3 : 4 (1980) pp. 489–507 MR0595748 Zbl 0472.47007 |
| [a4] | V. Vinnikov, "Commuting operators and function theory on a Riemann surface" S. Axler (ed.) J. McCarthy (ed.) D. Sarason (ed.) , Holomorphic Spaces and Their Operators , Math. Sci. Res. Inst. Publ. , 33 , Cambridge Univ. Press (1998) pp. 445–476 MR1634421 Zbl 0997.47007 |
Operator vessel. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Operator_vessel&oldid=50747