Operational calculus
One of the methods of mathematical analysis which in many cases makes it possible to reduce the study of differential operators, pseudo-differential operators and certain types of integral operators (cf. Differential operator; Integral operator; Pseudo-differential operator) and the solution of equations containing them, to an examination of simpler algebraic problems. The development and systematic use of operational calculus began with the work of O. Heaviside (1892), who proposed formal rules for dealing with the differentiation operator 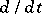 and solved a number of applied problems. However, he did not give operational calculus a mathematical basis; this was done with the aid of the Laplace transform; J. Mikusiński (1953) put operational calculus into algebraic form, using the concept of a function ring. The most general concept of an operational calculus is obtained using generalized functions (cf. Generalized function).
and solved a number of applied problems. However, he did not give operational calculus a mathematical basis; this was done with the aid of the Laplace transform; J. Mikusiński (1953) put operational calculus into algebraic form, using the concept of a function ring. The most general concept of an operational calculus is obtained using generalized functions (cf. Generalized function).
The simplest variant of operational calculus is as follows. Let 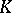 be the set of functions (with real or complex values) given in the domain
be the set of functions (with real or complex values) given in the domain 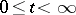 and absolutely integrable in any finite interval. The integral
and absolutely integrable in any finite interval. The integral
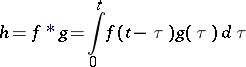 |
is called the convolution of the functions 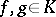 . With the usual addition operation and the operation of convolution,
. With the usual addition operation and the operation of convolution, 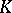 becomes a ring without zero divisors (Titchmarsh's theorem, 1924). Elements of the quotient field
becomes a ring without zero divisors (Titchmarsh's theorem, 1924). Elements of the quotient field 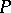 of this ring are called operators and are written as
of this ring are called operators and are written as 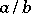 ; the fact that division in
; the fact that division in  is not always possible is precisely the source of a new concept, operators, which generalizes the concept of a function. To indicate the necessary difference in operational calculus between the concepts of a function and of its value at a point, the following notation is used:
is not always possible is precisely the source of a new concept, operators, which generalizes the concept of a function. To indicate the necessary difference in operational calculus between the concepts of a function and of its value at a point, the following notation is used:
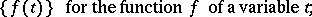 |
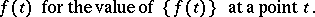 |
Examples of operators.
1) 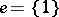 is the integration operator:
is the integration operator:
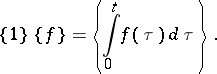 |
Moreover,
 |
and, in particular,
 |
 |
This is the Cauchy formula, a generalization of which to the case of an arbitrary (non-integer) index serves to define fractional integration.
2)  (where
(where  is a constant function) is a numerical operator; insofar as
is a constant function) is a numerical operator; insofar as 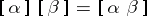 ,
, 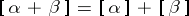 ,
,  , while
, while 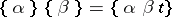 , numerical operators behave as ordinary numbers. Thus the operator is a generalization not only of a function, but also of a number;
, numerical operators behave as ordinary numbers. Thus the operator is a generalization not only of a function, but also of a number; 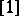 is the unit of the ring
is the unit of the ring 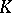 .
.
3) 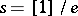 is the differentiation operator, the inverse of the integration operator. So, if a function
is the differentiation operator, the inverse of the integration operator. So, if a function 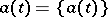 has a derivative
has a derivative 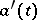 , then
, then
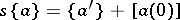 |
and
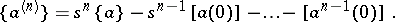 |
Hence, for example,
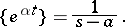 |
Of course, a non-differentiable function can be multiplied by the differentiation operator  ; however, the result will be, in general, an operator.
; however, the result will be, in general, an operator.
4)  is the algebraic derivative. It extends to arbitrary operators in the usual way. It appears that the action of this operator on a function of the differentiation operator
is the algebraic derivative. It extends to arbitrary operators in the usual way. It appears that the action of this operator on a function of the differentiation operator  coincides with differentiation with respect to
coincides with differentiation with respect to  .
.
Operational calculus provides suitable methods for the solution of linear differential equations, both ordinary and partial. For example, the solution of the equation
 |
satisfying the initial conditions  automatically reduces to an algebraic equation. It is expressed symbolically by the formula
automatically reduces to an algebraic equation. It is expressed symbolically by the formula
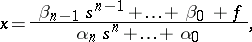 |
 |
The solution in its usual form is obtained by decomposition into elementary fractions with respect to the variable  , with subsequent inverse transformation by referring to appropriate function tables.
, with subsequent inverse transformation by referring to appropriate function tables.
In the use of operational calculus for partial differential equations (as well as for more general pseudo-differential equations), a differential and integral calculus of operator functions, i.e. functions with operator values, is employed. The concepts of continuity, derivative, convergence of series, integrals, etc., must be developed for these functions.
Let 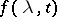 be a function defined for
be a function defined for 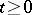 and
and 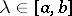 . A parametric operator function
. A parametric operator function 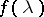 is defined by the formula
is defined by the formula 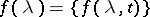 ; it places operators of a certain type — functions in
; it places operators of a certain type — functions in 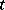 — in correspondence with the values of
— in correspondence with the values of 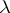 being considered. An operator function is said to be continuous for
being considered. An operator function is said to be continuous for 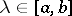 if it can be represented as the product of an operator
if it can be represented as the product of an operator 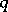 and a parametric function
and a parametric function 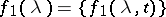 such that
such that 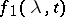 is continuous in the ordinary sense.
is continuous in the ordinary sense.
Examples.
1) Using the parametric function 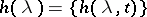 :
:
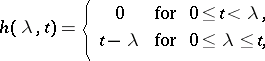 |
the Heaviside function is defined:
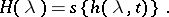 |
The values of the hyperbolic exponential function
 |
are called shift operators, since multiplication of a given function by 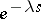 requires the displacement of its graph over
requires the displacement of its graph over 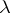 in the positive direction of the
in the positive direction of the 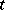 -axis.
-axis.
2) The solution of the heat equation
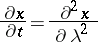 |
can be expressed using the parabolic exponential function (which is also a parametric operator function):
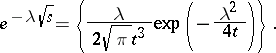 |
3) A periodic function 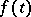 with period
with period 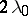 has the representation:
has the representation:
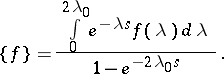 |
4) If 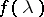 has numerical values in the interval
has numerical values in the interval 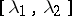 , then
, then
 |
i.e. multiplication of the given function 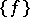 by
by 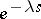 with subsequent integration entails a truncation of its graph. In particular,
with subsequent integration entails a truncation of its graph. In particular,
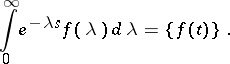 |
Thus, with each function 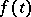 for which the integral being considered is convergent there is a corresponding analytic function:
for which the integral being considered is convergent there is a corresponding analytic function:
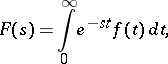 |
its Laplace transform. As a result, a fairly broad class of operators is described by functions of one parameter  ; moreover, this formal similarity is defined more exactly in mathematical terms by establishing a definite isomorphism.
; moreover, this formal similarity is defined more exactly in mathematical terms by establishing a definite isomorphism.
There are various generalizations of operational calculus; for example, operational calculus of differential operators other than 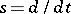 , for example,
, for example,  , which is based on other function rings with a properly defined product.
, which is based on other function rings with a properly defined product.
References
| [1] | V.A. Ditkin, A.P. Prudnikov, "Handbook of operational calculus" , Moscow (1965) (In Russian) |
| [2] | J. Mikusiński, "Operational calculus" , Pergamon (1959) (Translated from Polish) |
Comments
A second edition of [2] has recently appeared, [a1], [a2]. In the examples of parametric operator functions 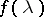 above, use is made of a differential and integral calculus for operators. For more details on the truncation of an operator function
above, use is made of a differential and integral calculus for operators. For more details on the truncation of an operator function 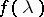 see [a2], Part V, Chapt. 1, § 5. For
see [a2], Part V, Chapt. 1, § 5. For 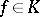 an operator of the form
an operator of the form 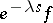 is identified with a Schwartz distribution with support bounded from below.
is identified with a Schwartz distribution with support bounded from below.
The notion of a Schwartz distribution and Mikusiński operator do not include each other, but both generalize the idea of a function and its derivatives.
The term "operational calculus" is also used in the sense of functional calculus; i.e. a homomorphism of a certain algebra of functions into an algebra of operators. Finally, the phrase "operational calculus" or "operator calculusoperator calculus" occurs in the context of the time-ordered operator calculus (Feynman–Dyson time-ordered operator calculus) developed in the 1950's for the study of quantum electrodynamics [a4], [a5], and relating to product integrals (cf. Product integral), [a6].
References
| [a1] | J. Mikusiński, "Operational calculus" , 1 , PWN & Pergamon (1987) (Translated from Polish) |
| [a2] | J. Mikusiński, Th.K. Boehme, "Operational calculus" , II , PWN & Pergamon (1987) |
| [a3] | B. van der Pol, H. Bremmer, "Operational calculus based on the two-sided Laplace integral" , Cambridge Univ. Press (1959) |
| [a4] | R.P. Feynman, "An operator calculus having applications in quantum electrodynamics" Phys. Rev. , 84 (1951) pp. 108–128 |
| [a5] | T.L. Gill, W.W. Zachary, "Time-ordered operators and Feynman–Dyson algebras" J. Math. Phys. , 28 (1987) pp. 1459–1470 |
| [a6] | J.D. Dollard, Ch.N. Friedman, "Product integration" , Addison-Wesley (1979) |
Operational calculus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Operational_calculus&oldid=15985