Normal form (for matrices)
The normal form of a matrix 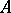 is a matrix
is a matrix 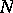 of a pre-assigned special form obtained from
of a pre-assigned special form obtained from 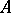 by means of transformations of a prescribed type. One distinguishes various normal forms, depending on the type of transformations in question, on the domain
by means of transformations of a prescribed type. One distinguishes various normal forms, depending on the type of transformations in question, on the domain 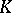 to which the coefficients of
to which the coefficients of 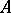 belong, on the form of
belong, on the form of 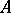 , and, finally, on the specific nature of the problem to be solved (for example, on the desirability of extending or not extending
, and, finally, on the specific nature of the problem to be solved (for example, on the desirability of extending or not extending  on transition from
on transition from 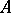 to
to 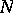 , on the necessity of determining
, on the necessity of determining 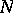 from
from 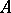 uniquely or with a certain amount of arbitrariness). Frequently, instead of "normal form" one uses the term "canonical form of a matrixcanonical form" . Among the classical normal forms are the following. (Henceforth
uniquely or with a certain amount of arbitrariness). Frequently, instead of "normal form" one uses the term "canonical form of a matrixcanonical form" . Among the classical normal forms are the following. (Henceforth 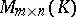 denotes the set of all matrices of
denotes the set of all matrices of 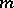 rows and
rows and  columns with coefficients in
columns with coefficients in 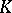 .)
.)
The Smith normal form.
Let 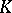 be either the ring of integers
be either the ring of integers 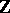 or the ring
or the ring 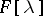 of polynomials in
of polynomials in 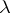 with coefficients in a field
with coefficients in a field 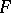 . A matrix
. A matrix 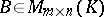 is called equivalent to a matrix
is called equivalent to a matrix 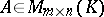 if there are invertible matrices
if there are invertible matrices  and
and 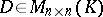 such that
such that 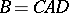 . Here
. Here 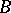 is equivalent to
is equivalent to 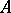 if and only if
if and only if 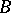 can be obtained from
can be obtained from 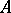 by a sequence of elementary row-and-column transformations, that is, transformations of the following three types: a) permutation of the rows (or columns); b) addition to one row (or column) of another row (or column) multiplied by an element of
by a sequence of elementary row-and-column transformations, that is, transformations of the following three types: a) permutation of the rows (or columns); b) addition to one row (or column) of another row (or column) multiplied by an element of 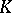 ; or c) multiplication of a row (or column) by an invertible element of
; or c) multiplication of a row (or column) by an invertible element of 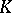 . For transformations of this kind the following propositions hold: Every matrix
. For transformations of this kind the following propositions hold: Every matrix 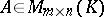 is equivalent to a matrix
is equivalent to a matrix 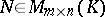 of the form
of the form
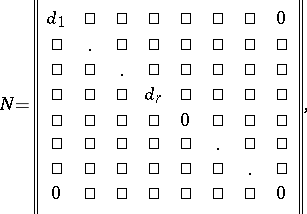 |
where 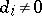 for all
for all 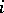 ;
; 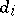 divides
divides 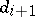 for
for 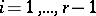 ; and if
; and if 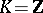 , then all
, then all 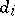 are positive; if
are positive; if 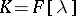 , then the leading coefficients of all polynomials
, then the leading coefficients of all polynomials 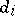 are 1. This matrix is called the Smith normal form of
are 1. This matrix is called the Smith normal form of 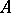 . The
. The 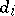 are called the invariant factors of
are called the invariant factors of 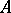 and the number
and the number  is called its rank. The Smith normal form of
is called its rank. The Smith normal form of 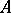 is uniquely determined and can be found as follows. The rank
is uniquely determined and can be found as follows. The rank  of
of 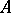 is the order of the largest non-zero minor of
is the order of the largest non-zero minor of 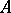 . Suppose that
. Suppose that 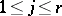 ; then among all minors of
; then among all minors of 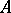 of order
of order 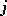 there is at least one non-zero. Let
there is at least one non-zero. Let 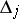 ,
, 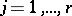 , be the greatest common divisor of all non-zero minors of
, be the greatest common divisor of all non-zero minors of 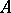 of order
of order 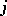 (normalized by the condition
(normalized by the condition 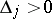 for
for 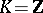 and such that the leading coefficient of
and such that the leading coefficient of 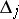 is 1 for
is 1 for 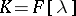 ), and let
), and let 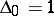 . Then
. Then 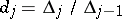 ,
, 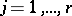 . The invariant factors form a full set of invariants of the classes of equivalent matrices: Two matrices in
. The invariant factors form a full set of invariants of the classes of equivalent matrices: Two matrices in 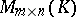 are equivalent if and only if their ranks and their invariant factors with equal indices are equal.
are equivalent if and only if their ranks and their invariant factors with equal indices are equal.
The invariant factors 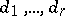 split (in a unique manner, up to the order of the factors) into the product of powers of irreducible elements
split (in a unique manner, up to the order of the factors) into the product of powers of irreducible elements  of
of 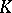 (which are positive integers
(which are positive integers 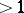 when
when 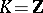 , and polynomials of positive degree with leading coefficient 1 when
, and polynomials of positive degree with leading coefficient 1 when 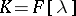 ):
):
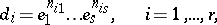 |
where the 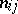 are non-negative integers. Every factor
are non-negative integers. Every factor 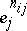 for which
for which 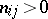 is called an elementary divisor of
is called an elementary divisor of 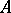 (over
(over 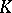 ). Every elementary divisor of
). Every elementary divisor of 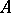 occurs in the set
occurs in the set 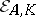 of all elementary divisors of
of all elementary divisors of 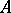 with multiplicity equal to the number of invariant factors having this divisor in their decompositions. In contrast to the invariant factors, the elementary divisors depend on the ring
with multiplicity equal to the number of invariant factors having this divisor in their decompositions. In contrast to the invariant factors, the elementary divisors depend on the ring 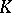 over which
over which 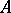 is considered: If
is considered: If 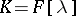 ,
, 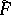 is an extension of
is an extension of 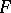 and
and 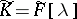 , then, in general, a matrix
, then, in general, a matrix 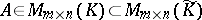 has distinct elementary divisors (but the same invariant factors), depending on whether
has distinct elementary divisors (but the same invariant factors), depending on whether  is regarded as an element of
is regarded as an element of 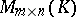 or of
or of 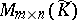 . The invariant factors can be recovered from the complete collection of elementary divisors, and vice versa.
. The invariant factors can be recovered from the complete collection of elementary divisors, and vice versa.
For a practical method of finding the Smith normal form see, for example, [1].
The main result on the Smith normal form was obtained for 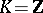 (see [7]) and
(see [7]) and 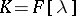 (see [8]). With practically no changes, the theory of Smith normal forms goes over to the case when
(see [8]). With practically no changes, the theory of Smith normal forms goes over to the case when 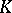 is any principal ideal ring (see [3], [6]). The Smith normal form has important applications; for example, the structure theory of finitely-generated modules over principal ideal rings is based on it (see [3], [6]); in particular, this holds for the theory of finitely-generated Abelian groups and theory of the Jordan normal form (see below).
is any principal ideal ring (see [3], [6]). The Smith normal form has important applications; for example, the structure theory of finitely-generated modules over principal ideal rings is based on it (see [3], [6]); in particular, this holds for the theory of finitely-generated Abelian groups and theory of the Jordan normal form (see below).
The natural normal form.
Let 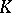 be a field. Two square matrices
be a field. Two square matrices 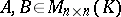 are called similar over
are called similar over 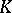 if there is a non-singular matrix
if there is a non-singular matrix 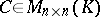 such that
such that 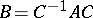 . There is a close link between similarity and equivalence: Two matrices
. There is a close link between similarity and equivalence: Two matrices 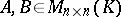 are similar if and only if the matrices
are similar if and only if the matrices 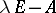 and
and 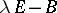 , where
, where 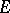 is the identity matrix, are equivalent. Thus, for the similarity of
is the identity matrix, are equivalent. Thus, for the similarity of 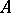 and
and 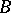 it is necessary and sufficient that all invariant factors, or, what is the same, the collection of elementary divisors over
it is necessary and sufficient that all invariant factors, or, what is the same, the collection of elementary divisors over 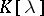 of
of 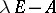 and
and 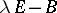 , are the same. For a practical method of finding a
, are the same. For a practical method of finding a 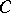 for similar matrices
for similar matrices 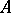 and
and 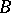 , see [1], [4].
, see [1], [4].
The matrix 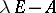 is called the characteristic matrix of
is called the characteristic matrix of 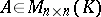 , and the invariant factors of
, and the invariant factors of 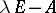 are called the similarity invariants of
are called the similarity invariants of 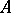 ; there are
; there are  of them, say
of them, say 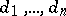 . The polynomial
. The polynomial 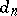 is the determinant of
is the determinant of 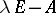 and is called the characteristic polynomial of
and is called the characteristic polynomial of 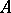 . Suppose that
. Suppose that 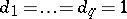 and that for
and that for 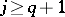 the degree of
the degree of 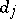 is greater than 1. Then
is greater than 1. Then 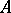 is similar over
is similar over 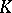 to a block-diagonal matrix
to a block-diagonal matrix 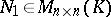 of the form
of the form
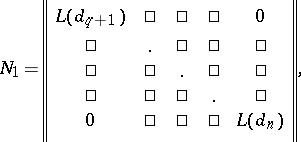 |
where 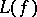 for a polynomial
for a polynomial
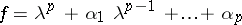 |
denotes the so-called companion matrix
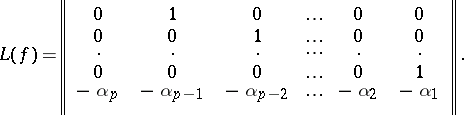 |
The matrix 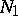 is uniquely determined from
is uniquely determined from 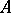 and is called the first natural normal form of
and is called the first natural normal form of 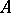 (see [1], [2]).
(see [1], [2]).
Now let 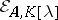 be the collection of all elementary divisors of
be the collection of all elementary divisors of 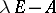 . Then
. Then 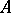 is similar over
is similar over 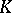 to a block-diagonal matrix
to a block-diagonal matrix 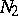 (cf. Block-diagonal operator) whose blocks are the companion matrices of all elementary divisors
(cf. Block-diagonal operator) whose blocks are the companion matrices of all elementary divisors 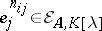 of
of 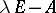 :
:
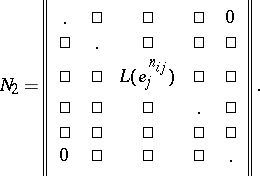 |
The matrix 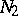 is determined from
is determined from 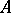 only up to the order of the blocks along the main diagonal; it is called the second natural normal form of
only up to the order of the blocks along the main diagonal; it is called the second natural normal form of 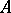 (see [1], [2]), or its Frobenius, rational or quasi-natural normal form (see [4]). In contrast to the first, the second natural form changes, generally speaking, on transition from
(see [1], [2]), or its Frobenius, rational or quasi-natural normal form (see [4]). In contrast to the first, the second natural form changes, generally speaking, on transition from 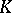 to an extension.
to an extension.
The Jordan normal form.
Let 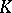 be a field, let
be a field, let 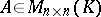 , and let
, and let 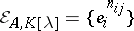 be the collection of all elementary divisors of
be the collection of all elementary divisors of 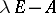 over
over 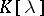 . Suppose that
. Suppose that 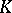 has the property that the characteristic polynomial
has the property that the characteristic polynomial 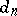 of
of 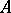 splits in
splits in 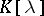 into linear factors. (This is so, for example, if
into linear factors. (This is so, for example, if 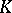 is the field of complex numbers or, more generally, any algebraically closed field.) Then every one of the polynomials
is the field of complex numbers or, more generally, any algebraically closed field.) Then every one of the polynomials 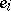 has the form
has the form 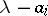 for some
for some 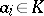 , and, accordingly,
, and, accordingly, 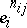 has the form
has the form 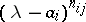 . The matrix
. The matrix 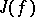 in
in 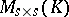 of the form
of the form
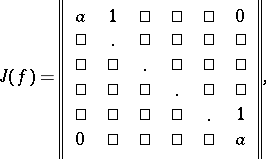 |
where 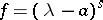 ,
, 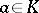 , is called the hypercompanion matrix of
, is called the hypercompanion matrix of 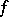 (see [1]) or the Jordan block of order
(see [1]) or the Jordan block of order  with eigenvalue
with eigenvalue  . The following fundamental proposition holds: A matrix
. The following fundamental proposition holds: A matrix 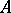 is similar over
is similar over 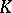 to a block-diagonal matrix
to a block-diagonal matrix 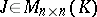 whose blocks are the hypercompanion matrices of all elementary divisors of
whose blocks are the hypercompanion matrices of all elementary divisors of 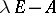 :
:
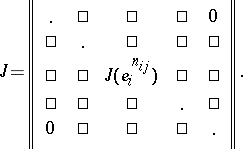 |
The matrix 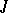 is determined only up to the order of the blocks along the main diagonal; it is a Jordan matrix and is called the Jordan normal form of
is determined only up to the order of the blocks along the main diagonal; it is a Jordan matrix and is called the Jordan normal form of 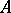 . If
. If 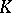 does not have the property mentioned above, then
does not have the property mentioned above, then 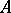 cannot be brought, over
cannot be brought, over 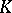 , to the Jordan normal form (but it can over a finite extension of
, to the Jordan normal form (but it can over a finite extension of 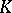 ). See [4] for information about the so-called generalized Jordan normal form, reduction to which is possible over any field
). See [4] for information about the so-called generalized Jordan normal form, reduction to which is possible over any field 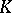 .
.
Apart from the various normal forms for arbitrary matrices, there are also special normal forms of special matrices. Classical examples are the normal forms of symmetric and skew-symmetric matrices. Let 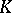 be a field. Two matrices
be a field. Two matrices 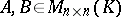 are called congruent (see [1]) if there is a non-singular matrix
are called congruent (see [1]) if there is a non-singular matrix 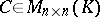 such that
such that 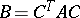 . Normal forms under the congruence relation have been investigated most thoroughly for the classes of symmetric and skew-symmetric matrices. Suppose that
. Normal forms under the congruence relation have been investigated most thoroughly for the classes of symmetric and skew-symmetric matrices. Suppose that 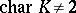 and that
and that 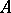 is skew-symmetric, that is,
is skew-symmetric, that is, 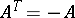 . Then
. Then 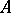 is congruent to a uniquely determined matrix
is congruent to a uniquely determined matrix 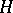 of the form
of the form
 |
which can be regarded as the normal form of 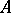 under congruence. If
under congruence. If 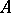 is symmetric, that is,
is symmetric, that is, 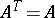 , then it is congruent to a matrix
, then it is congruent to a matrix 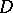 of the form
of the form
 |
where 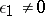 for all
for all  . The number
. The number  is the rank of
is the rank of 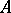 and is uniquely determined. The subsequent finer choice of the
and is uniquely determined. The subsequent finer choice of the 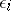 depends on the properties of
depends on the properties of 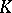 . Thus, if
. Thus, if 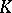 is algebraically closed, one may assume that
is algebraically closed, one may assume that  ; if
; if 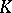 is the field of real numbers, one may assume that
is the field of real numbers, one may assume that 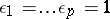 and
and 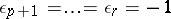 for a certain
for a certain 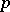 .
. 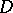 is uniquely determined by these properties and can be regarded as the normal form of
is uniquely determined by these properties and can be regarded as the normal form of 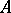 under congruence. See [6], [10] and Quadratic form for information about the normal forms of symmetric matrices for a number of other fields, and also about Hermitian analogues of this theory.
under congruence. See [6], [10] and Quadratic form for information about the normal forms of symmetric matrices for a number of other fields, and also about Hermitian analogues of this theory.
A common feature in the theories of normal forms considered above (and also in others) is the fact that the admissible transformations over the relevant set of matrices are determined by the action of a certain group, so that the classes of matrices that can be carried into each other by means of these transformations are the orbits (cf. Orbit) of this group, and the appropriate normal form is the result of selecting in each orbit a certain canonical representative. Thus, the classes of equivalent matrices are the orbits of the group 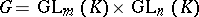 (where
(where 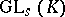 is the group of invertible square matrices of order
is the group of invertible square matrices of order  with coefficients in
with coefficients in 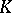 ), acting on
), acting on 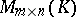 by the rule
by the rule 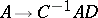 , where
, where 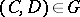 . The classes of similar matrices are the orbits of
. The classes of similar matrices are the orbits of 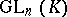 on
on 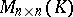 acting by the rule
acting by the rule 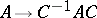 , where
, where 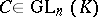 . The classes of congruent symmetric or skew-symmetric matrices are the orbits of the group
. The classes of congruent symmetric or skew-symmetric matrices are the orbits of the group 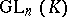 on the set of all symmetric or skew-symmetric matrices of order
on the set of all symmetric or skew-symmetric matrices of order  , acting by the rule
, acting by the rule 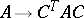 , where
, where 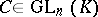 . From this point of view every normal form is a specific example of the solution of part of the general problem of orbital decomposition for the action of a certain transformation group.
. From this point of view every normal form is a specific example of the solution of part of the general problem of orbital decomposition for the action of a certain transformation group.
References
| [1] | M. Markus, "A survey of matrix theory and matrix inequalities" , Allyn & Bacon (1964) |
| [2] | P. Lancaster, "Theory of matrices" , Acad. Press (1969) MR0245579 Zbl 0186.05301 |
| [3] | S. Lang, "Algebra" , Addison-Wesley (1974) MR0783636 Zbl 0712.00001 |
| [4] | A.I. Mal'tsev, "Foundations of linear algebra" , Freeman (1963) (Translated from Russian) Zbl 0396.15001 |
| [5] | N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French) MR0643362 Zbl 1139.12001 |
| [6] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) MR0354207 |
| [7] | H.J.S. Smith, "On systems of linear indeterminate equations and congruences" , Collected Math. Papers , 1 , Chelsea, reprint (1979) pp. 367–409 |
| [8] | G. Frobenius, "Theorie der linearen Formen mit ganzen Coeffizienten" J. Reine Angew. Math. , 86 (1879) pp. 146–208 |
| [9] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian) MR1657129 MR0107649 MR0107648 Zbl 0927.15002 Zbl 0927.15001 Zbl 0085.01001 |
| [10] | J.-P. Serre, "A course in arithmetic" , Springer (1973) (Translated from French) MR0344216 Zbl 0256.12001 |
Comments
The Smith canonical form and a canonical form related to the first natural normal form are of substantial importance in linear control and system theory [a1], [a2]. Here one studies systems of equations 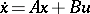 ,
,  ,
, 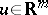 , and the similarity relation is:
, and the similarity relation is:  . A pair of matrices
. A pair of matrices 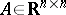 ,
, 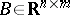 is called completely controllable if the rank of the block matrix
is called completely controllable if the rank of the block matrix
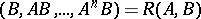 |
is  . Observe that
. Observe that 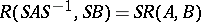 , so that a canonical form can be formed by selecting
, so that a canonical form can be formed by selecting  independent column vectors from
independent column vectors from 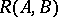 . This can be done in many ways. The most common one is to test the columns of
. This can be done in many ways. The most common one is to test the columns of 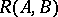 for independence in the order in which they appear in
for independence in the order in which they appear in 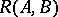 . This yields the following so-called Brunovskii–Luenberger canonical form or block companion canonical form for a completely-controllable pair
. This yields the following so-called Brunovskii–Luenberger canonical form or block companion canonical form for a completely-controllable pair 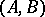 :
:
 |
 |
where 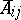 is a matrix of size
is a matrix of size 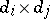 for certain
for certain 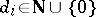 ,
, 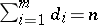 , of the form
, of the form
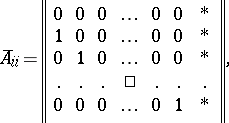 |
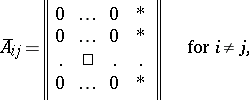 |
and 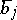 for
for 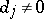 is the
is the 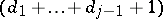 -th standard basis vector of
-th standard basis vector of 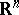 ; the
; the 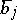 with
with 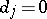 have arbitrary coefficients
have arbitrary coefficients  . Here the
. Here the  's denote coefficients which can take any value. If
's denote coefficients which can take any value. If 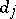 or
or 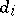 is zero, the block
is zero, the block 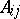 is empty (does not occur). Instead of
is empty (does not occur). Instead of 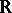 any field can be used. The
any field can be used. The 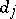 are called controllability indices or Kronecker indices. They are invariants.
are called controllability indices or Kronecker indices. They are invariants.
Canonical forms are often used in (numerical) computations. This must be done with caution, because they may not depend continuously on the parameters [a3]. For example, the Jordan canonical form is not continuous; an example of this is:
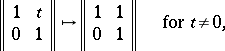 |
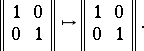 |
The matter of continuous canonical forms has much to do with moduli problems (cf. Moduli theory). Related is the matter of canonical forms for families of objects, e.g. canonical forms for holomorphic families of matrices under similarity [a4]. For a survey of moduli-type questions in linear control theory cf. [a5].
In the case of a controllable pair 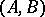 with
with 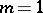 , i.e.
, i.e. 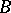 is a vector
is a vector 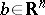 , the matrix
, the matrix 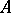 is cyclic, see also the section below on normal forms for operators. In this special case there is just one block
is cyclic, see also the section below on normal forms for operators. In this special case there is just one block 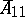 (and one vector
(and one vector 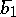 ). This canonical form for a cyclic matrix with a cyclic vector is also called the Frobenius canonical form or the companion canonical form.
). This canonical form for a cyclic matrix with a cyclic vector is also called the Frobenius canonical form or the companion canonical form.
References
| [a1] | W.A. Wolovich, "Linear multivariable systems" , Springer (1974) MR0359881 Zbl 0291.93002 |
| [a2] | J. Klamka, "Controllability of dynamical systems" , Kluwer (1990) MR2461640 MR1325771 MR1134783 MR0707724 MR0507539 Zbl 0911.93015 Zbl 0876.93016 Zbl 0930.93008 Zbl 1043.93509 Zbl 0853.93020 Zbl 0852.93007 Zbl 0818.93002 Zbl 0797.93004 Zbl 0814.93012 Zbl 0762.93006 Zbl 0732.93008 Zbl 0671.93040 Zbl 0667.93007 Zbl 0666.93009 Zbl 0509.93012 Zbl 0393.93041 |
| [a3] | S.H. Golub, J.H. Wilkinson, "Ill conditioned eigensystems and the computation of the Jordan canonical form" SIAM Rev. , 18 (1976) pp. 578–619 MR0413456 Zbl 0341.65027 |
| [a4] | V.I. Arnol'd, "On matrices depending on parameters" Russ. Math. Surv. , 26 : 2 (1971) pp. 29–43 Uspekhi Mat. Nauk , 26 : 2 (1971) pp. 101–114 Zbl 0259.15011 |
| [a5] | M. Hazewinkel, "(Fine) moduli spaces for linear systems: what are they and what are they good for" C.I. Byrnes (ed.) C.F. Martin (ed.) , Geometrical Methods for the Theory of Linear Systems , Reidel (1980) pp. 125–193 MR0608993 Zbl 0481.93023 |
| [a6] | H.W. Turnball, A.C. Aitken, "An introduction to the theory of canonical matrices" , Blackie & Son (1932) |
A normal form of an operator is a representation, up to an isomorphism, of a self-adjoint operator 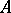 acting on a Hilbert space
acting on a Hilbert space 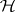 as an orthogonal sum of multiplication operators by the independent variable.
as an orthogonal sum of multiplication operators by the independent variable.
To begin with, suppose that 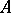 is a cyclic operator; this means that there is an element
is a cyclic operator; this means that there is an element 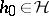 such that every element
such that every element 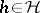 has a unique representation in the form
has a unique representation in the form  , where
, where 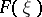 is a function for which
is a function for which
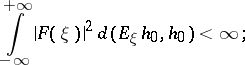 |
here 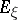 ,
, 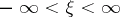 , is the spectral resolution of
, is the spectral resolution of 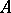 . Let
. Let 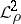 be the space of square-integrable functions on
be the space of square-integrable functions on 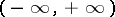 with weight
with weight 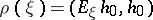 , and let
, and let 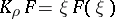 be the multiplication operator by the independent variable, with domain of definition
be the multiplication operator by the independent variable, with domain of definition
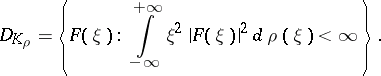 |
Then the operators 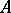 and
and 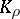 are isomorphic,
are isomorphic, 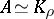 ; that is, there exists an isomorphic and isometric mapping
; that is, there exists an isomorphic and isometric mapping 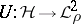 such that
such that 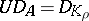 and
and 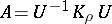 .
.
Suppose, next, that 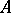 is an arbitrary self-adjoint operator. Then
is an arbitrary self-adjoint operator. Then 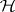 can be split into an orthogonal sum of subspaces
can be split into an orthogonal sum of subspaces 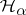 on each of which
on each of which 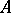 induces a cyclic operator
induces a cyclic operator 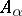 , so that
, so that 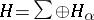 ,
, 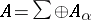 and
and 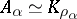 . If the operator
. If the operator 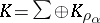 is given on
is given on 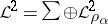 , then
, then 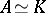 .
.
The operator 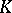 is called the normal form or canonical representation of
is called the normal form or canonical representation of 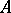 . The theorem on the canonical representation extends to the case of arbitrary normal operators (cf. Normal operator).
. The theorem on the canonical representation extends to the case of arbitrary normal operators (cf. Normal operator).
References
| [1] | A.I. Plesner, "Spectral theory of linear operators" , F. Ungar (1965) (Translated from Russian) MR0194900 Zbl 0188.44402 Zbl 0185.21002 |
| [2] | N.I. Akhiezer, I.M. Glazman, "Theory of linear operators in Hilbert spaces" , 1–2 , Pitman (1981) (Translated from Russian) MR0615737 MR0615736 |
V.I. Sobolev
The normal form of an operator 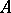 is a representation of
is a representation of 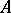 , acting on a Fock space constructed over a certain space
, acting on a Fock space constructed over a certain space 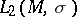 , where
, where 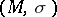 is a measure space, in the form of a sum
is a measure space, in the form of a sum
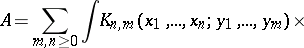 | (1) |
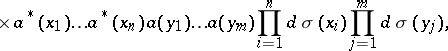 |
where 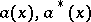 (
(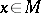 ) are operator-valued generalized functions generating families of annihilation operators
) are operator-valued generalized functions generating families of annihilation operators 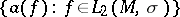 and creation operators
and creation operators 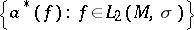 :
:
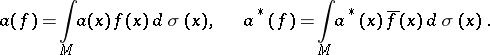 |
In each term of expression (1) all factors 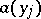 ,
, 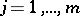 , stand to the right of all factors
, stand to the right of all factors 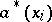 ,
, 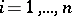 , and the (possibly generalized) functions
, and the (possibly generalized) functions 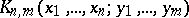 in the two sets of variables
in the two sets of variables 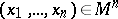 ,
, 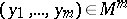 ,
, 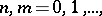 are, in the case of a symmetric (Boson) Fock space, symmetric in the variables of each set separately, and, in the case of an anti-symmetric (Fermion) Fock space, anti-symmetric in these variables.
are, in the case of a symmetric (Boson) Fock space, symmetric in the variables of each set separately, and, in the case of an anti-symmetric (Fermion) Fock space, anti-symmetric in these variables.
For any bounded operator 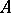 the normal form exists and is unique.
the normal form exists and is unique.
The representation (1) can be rewritten in a form containing the annihilation and creation operators directly:
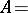 | (2) |
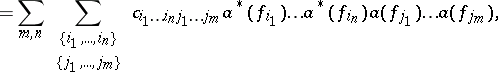 |
where 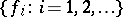 is an orthonormal basis in
is an orthonormal basis in 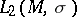 and the summation in (2) is over all pairs of finite collections
and the summation in (2) is over all pairs of finite collections 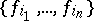 ,
, 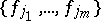 of elements of this basis.
of elements of this basis.
In the case of an arbitrary (separable) Hilbert space 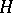 the normal form of an operator
the normal form of an operator 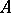 acting on the Fock space
acting on the Fock space 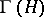 constructed over
constructed over 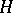 is determined for a fixed basis
is determined for a fixed basis 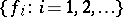 in
in 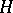 by means of the expression (2), where
by means of the expression (2), where 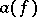 ,
, 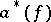 ,
, 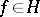 , are families of annihilation and creation operators acting on
, are families of annihilation and creation operators acting on 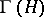 .
.
References
| [1] | F.A. Berezin, "The method of second quantization" , Acad. Press (1966) (Translated from Russian) (Revised (augmented) second edition: Kluwer, 1989) MR0208930 Zbl 0151.44001 |
R.A. Minlos
Comments
References
| [a1] | N.N. [N.N. Bogolyubov] Bogolubov, A.A. Logunov, I.T. Todorov, "Introduction to axiomatic quantum field theory" , Benjamin (1975) (Translated from Russian) MR0452276 MR0452277 |
| [a2] | G. Källen, "Quantum electrodynamics" , Springer (1972) MR0153346 MR0056465 MR0051156 MR0039581 Zbl 0116.45005 Zbl 0074.44202 Zbl 0050.43001 Zbl 0046.21402 Zbl 0041.57104 |
| [a3] | J. Glimm, A. Jaffe, "Quantum physics, a functional integral point of view" , Springer (1981) Zbl 0461.46051 |
The normal form of a recursive function is a method for specifying an  -place recursive function
-place recursive function 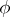 in the form
in the form
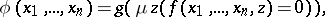 | (*) |
where 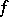 is an
is an 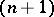 -place primitive recursive function,
-place primitive recursive function, 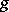 is a
is a 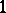 -place primitive recursive function and
-place primitive recursive function and 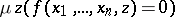 is the result of applying the least-number operator to
is the result of applying the least-number operator to 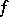 . Kleene's normal form theorem asserts that there is a primitive recursive function
. Kleene's normal form theorem asserts that there is a primitive recursive function 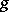 such that every recursive function
such that every recursive function 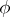 can be represented in the form (*) with a suitable function
can be represented in the form (*) with a suitable function 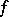 depending on
depending on 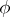 ; that is,
; that is,
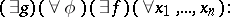 |
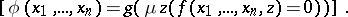 |
The normal form theorem is one of the most important results in the theory of recursive functions.
A.A. Markov [2] obtained a characterization of those functions 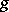 that can be used in the normal form theorem for the representation (*). A function
that can be used in the normal form theorem for the representation (*). A function 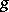 can be used as function whose existence is asserted in the normal form theorem if and only if the equation
can be used as function whose existence is asserted in the normal form theorem if and only if the equation 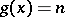 has infinitely many solutions for each
has infinitely many solutions for each  . Such functions are called functions of great range.
. Such functions are called functions of great range.
References
| [1] | A.I. Mal'tsev, "Algorithms and recursive functions" , Wolters-Noordhoff (1970) (Translated from Russian) Zbl 0198.02501 |
| [2] | A.A. Markov, "On the representation of recursive functions" Izv. Akad. Nauk SSSR Ser. Mat. , 13 : 5 (1949) pp. 417–424 (In Russian) MR0031444 |
V.E. Plisko
Comments
References
| [a1] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951) pp. 288 MR1234051 MR1570642 MR0051790 Zbl 0875.03002 Zbl 0604.03002 Zbl 0109.00509 Zbl 0047.00703 |
A normal form of a system of differential equations
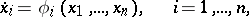 | (1) |
near an invariant manifold 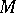 is a formal system
is a formal system
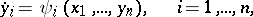 | (2) |
that is obtained from (1) by an invertible formal change of coordinates
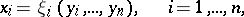 | (3) |
in which the Taylor–Fourier series 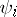 contain only resonance terms. In a particular case, normal forms occurred first in the dissertation of H. Poincaré (see [1]). By means of a normal form (2) some systems (1) can be integrated, and many can be investigated for stability and can be integrated approximately; for systems (1) a search has been made for periodic solutions and families of conditionally periodic solutions, and their bifurcation has been studied.
contain only resonance terms. In a particular case, normal forms occurred first in the dissertation of H. Poincaré (see [1]). By means of a normal form (2) some systems (1) can be integrated, and many can be investigated for stability and can be integrated approximately; for systems (1) a search has been made for periodic solutions and families of conditionally periodic solutions, and their bifurcation has been studied.
Normal forms in a neighbourhood of a fixed point.
Suppose that 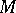 contains a fixed point
contains a fixed point 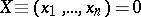 of the system (1) (that is,
of the system (1) (that is, 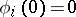 ), that the
), that the 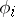 are analytic at it and that
are analytic at it and that 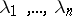 are the eigen values of the matrix
are the eigen values of the matrix 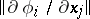 for
for 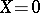 . Let
. Let 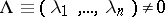 . Then in a full neighbourhood of
. Then in a full neighbourhood of 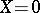 the system (1) has the following normal form (2): the matrix
the system (1) has the following normal form (2): the matrix 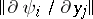 has for
has for 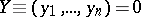 a normal form (for example, the Jordan normal form) and the Taylor series
a normal form (for example, the Jordan normal form) and the Taylor series
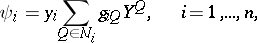 | (4) |
contain only resonance terms for which
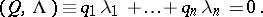 | (5) |
Here 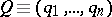 ,
, 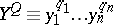 ,
, 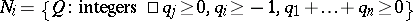 . If equation (5) has no solutions
. If equation (5) has no solutions 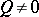 in
in 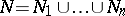 , then the normal form (2) is linear:
, then the normal form (2) is linear:
 |
Every system (1) with 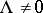 can be reduced in a neighbourhood of a fixed point to its normal form (2) by some formal transformation (3), where the
can be reduced in a neighbourhood of a fixed point to its normal form (2) by some formal transformation (3), where the 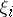 are (possibly divergent) power series,
are (possibly divergent) power series, 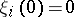 and
and 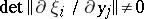 for
for 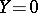 .
.
Generally speaking, the normalizing transformation (3) and the normal form (2) (that is, the coefficients 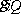 in (4)) are not uniquely determined by the original system (1). A normal form (2) preserves many properties of the system (1), such as being real, symmetric, Hamiltonian, etc. (see , [3]). If the original system contains small parameters, one can include them among the coordinates
in (4)) are not uniquely determined by the original system (1). A normal form (2) preserves many properties of the system (1), such as being real, symmetric, Hamiltonian, etc. (see , [3]). If the original system contains small parameters, one can include them among the coordinates 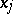 , and then
, and then 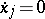 . Such coordinates do not change under a normalizing transformation (see [3]).
. Such coordinates do not change under a normalizing transformation (see [3]).
If 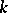 is the number of linearly independent solutions
is the number of linearly independent solutions 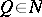 of equation (5), then by means of a transformation
of equation (5), then by means of a transformation
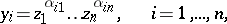 |
where the 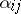 are integers and
are integers and 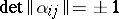 , the normal form (2) is carried to a system
, the normal form (2) is carried to a system
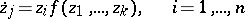 |
(see , [3]). The solution of this system reduces to a solution of the subsystem of the first 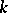 equations and to
equations and to 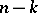 quadratures. The subsystem has to be investigated in the neighbourhood of the multiple singular point
quadratures. The subsystem has to be investigated in the neighbourhood of the multiple singular point 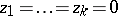 , because the
, because the 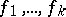 do not contain linear terms. This can be done by a local method (see [3]).
do not contain linear terms. This can be done by a local method (see [3]).
The following problem has been examined (see ): Under what conditions on the normal form (2) does the normalizing transformation of an analytic system (1) converge (be analytic)? Let
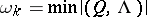 |
for those 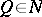 for which
for which
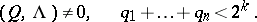 |
Condition 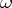 :
: 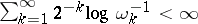 .
.
Condition 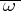 :
:  as
as 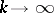 .
.
Condition 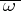 is weaker than
is weaker than 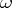 . Both are satisfied for almost-all
. Both are satisfied for almost-all 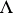 (relative to Lebesgue measure) and are very weak arithmetic restrictions on
(relative to Lebesgue measure) and are very weak arithmetic restrictions on 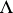 .
.
In case 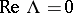 there is also condition
there is also condition 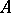 (for the general case, see in ): There exists a power series
(for the general case, see in ): There exists a power series 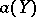 such that in (4),
such that in (4), 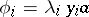 ,
, 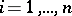 .
.
If for an analytic system (1) 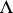 satisfies condition
satisfies condition 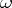 and the normal form (2) satisfies condition
and the normal form (2) satisfies condition 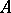 , then there exists an analytic transformation of (1) to a certain normal form. If (2) is obtained from an analytic system and fails to satisfy either condition
, then there exists an analytic transformation of (1) to a certain normal form. If (2) is obtained from an analytic system and fails to satisfy either condition 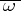 or condition
or condition 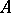 , then there exists an analytic system (1) that has (2) as its normal form, and every transformation to a normal form diverges (is not analytic).
, then there exists an analytic system (1) that has (2) as its normal form, and every transformation to a normal form diverges (is not analytic).
Thus, the problem raised above is solved for all normal forms except those for which 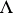 satisfies condition
satisfies condition 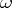 , but not
, but not 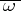 , while the remaining coefficients of the normal form satisfy condition
, while the remaining coefficients of the normal form satisfy condition 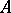 . The latter is a very rigid restriction on the coefficients of a normal form, and for large
. The latter is a very rigid restriction on the coefficients of a normal form, and for large  it holds, generally speaking, only in degenerate cases. That is, the basic reason for divergence of a transformation to normal form is not small denominators, but degeneracy of the normal form.
it holds, generally speaking, only in degenerate cases. That is, the basic reason for divergence of a transformation to normal form is not small denominators, but degeneracy of the normal form.
But even in cases of divergence of the normalizing transformation (3) with respect to (2), one can study properties of the solutions of the system (1). For example, a real system (1) has a smooth transformation to the normal form (2) even when it is not analytic. The majority of results on smooth normalization have been obtained under the condition that all 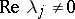 . Under this condition, with the help of a change
. Under this condition, with the help of a change 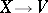 of finite smoothness class, a system (1) can be brought to a truncated normal form
of finite smoothness class, a system (1) can be brought to a truncated normal form
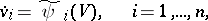 | (6) |
where the 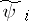 are polynomials of degree
are polynomials of degree 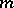 (see [4]–). If in the normalizing transformation (3) all terms of degree higher than
(see [4]–). If in the normalizing transformation (3) all terms of degree higher than 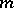 are discarded, the result is a transformation
are discarded, the result is a transformation
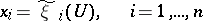 | (7) |
(the 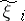 are polynomials), that takes (1) to the form
are polynomials), that takes (1) to the form
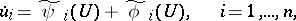 | (8) |
where the 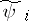 are polynomials containing only resonance terms and the
are polynomials containing only resonance terms and the 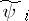 are convergent power series containing only terms of degree higher than
are convergent power series containing only terms of degree higher than 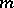 . Solutions of the truncated normal form (6) are approximations for solutions of (8) and, after the transformation (7), give approximations of solutions of the original system (1). In many cases one succeeds in constructing for (6) a Lyapunov function (or Chetaev function)
. Solutions of the truncated normal form (6) are approximations for solutions of (8) and, after the transformation (7), give approximations of solutions of the original system (1). In many cases one succeeds in constructing for (6) a Lyapunov function (or Chetaev function) 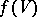 such that
such that
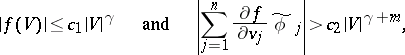 |
where 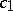 and
and 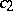 are positive constants. Then
are positive constants. Then 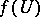 is a Lyapunov (Chetaev) function for the system (8); that is, the point
is a Lyapunov (Chetaev) function for the system (8); that is, the point 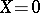 is stable (unstable). For example, if all
is stable (unstable). For example, if all 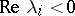 , one can take
, one can take 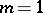 ,
, 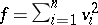 and obtain Lyapunov's theorem on stability under linear approximation (see [7]; for other examples see the survey [8]).
and obtain Lyapunov's theorem on stability under linear approximation (see [7]; for other examples see the survey [8]).
From the normal form (2) one can find invariant analytic sets of the system (1). In what follows it is assumed for simplicity of exposition that 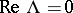 . From the normal form (2) one extracts the formal set
. From the normal form (2) one extracts the formal set
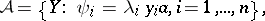 |
where  is a free parameter. Condition
is a free parameter. Condition 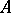 is satisfied on the set
is satisfied on the set 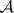 . Let
. Let 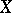 be the union of subspaces of the form
be the union of subspaces of the form  such that the corresponding eigen values
such that the corresponding eigen values 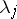 ,
, 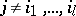 ,
, 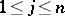 , are pairwise commensurable. The formal set
, are pairwise commensurable. The formal set 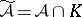 is analytic in the system (1). From
is analytic in the system (1). From 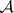 one selects the subset
one selects the subset 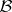 that is analytic in (1) if condition
that is analytic in (1) if condition 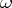 holds (see [3]). On the sets
holds (see [3]). On the sets 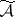 and
and 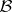 lie periodic solutions and families of conditionally-periodic solutions of (1). By considering the sets
lie periodic solutions and families of conditionally-periodic solutions of (1). By considering the sets 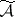 and
and 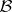 in systems with small parameters, one can study all analytic perturbations and bifurcations of such solutions (see [9]).
in systems with small parameters, one can study all analytic perturbations and bifurcations of such solutions (see [9]).
Generalizations.
If a system (1) does not lead to a normal form (2) but to a system whose right-hand sides contain certain non-resonance terms, then the resulting simplification is less substantial, but can improve the quality of the transformation. Thus, the reduction to a "semi-normal form" is analytic under a weakened condition 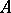 (see ). Another version is a transformation that normalizes a system (1) only on certain submanifolds (for example, on certain coordinate subspaces; see ). A combination of these approaches makes it possible to prove for (1) the existence of invariant submanifolds and of solutions of specific form (see [9]).
(see ). Another version is a transformation that normalizes a system (1) only on certain submanifolds (for example, on certain coordinate subspaces; see ). A combination of these approaches makes it possible to prove for (1) the existence of invariant submanifolds and of solutions of specific form (see [9]).
Suppose that a system (1) is defined and analytic in a neighbourhood of an invariant manifold 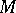 of dimension
of dimension 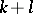 that is fibred into
that is fibred into 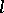 -dimensional invariant tori. Then close to
-dimensional invariant tori. Then close to 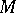 one can introduce local coordinates
one can introduce local coordinates
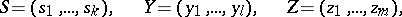 |
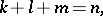 |
such that 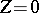 on
on 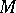 ,
, 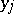 is of period
is of period 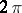 ,
, 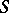 ranges over a certain domain
ranges over a certain domain 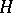 , and (1) takes the form
, and (1) takes the form
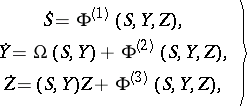 | (9) |
where 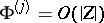 ,
, 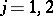 ,
, 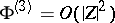 and
and 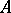 is a matrix. If
is a matrix. If 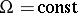 and
and 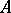 is triangular with constant main diagonal
is triangular with constant main diagonal 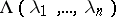 , then (under a weak restriction on the small denominators) there is a formal transformation of the local coordinates
, then (under a weak restriction on the small denominators) there is a formal transformation of the local coordinates 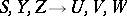 that takes the system (9) to the normal form
that takes the system (9) to the normal form
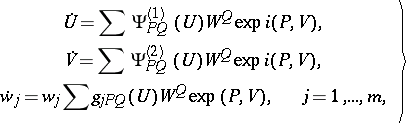 | (10) |
where 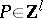 ,
, 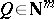 ,
, 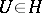 , and
, and 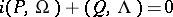 .
.
If among the coordinates 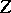 there is a small parameter, (9) can be averaged by the Krylov–Bogolyubov method of averaging (see [10]), and the averaged system is a normal form. More generally, perturbation theory can be regarded as a special case of the theory of normal forms, when one of the coordinates is a small parameter (see [11]).
there is a small parameter, (9) can be averaged by the Krylov–Bogolyubov method of averaging (see [10]), and the averaged system is a normal form. More generally, perturbation theory can be regarded as a special case of the theory of normal forms, when one of the coordinates is a small parameter (see [11]).
Theorems on the convergence of a normalizing change, on the existence of analytic invariant sets, etc., carry over to the systems (9) and (10). Here the best studied case is when 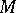 is a periodic solution, that is,
is a periodic solution, that is, 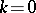 ,
, 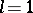 . In this case the theory of normal forms is in many respects identical with the case when
. In this case the theory of normal forms is in many respects identical with the case when 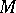 is a fixed point. Poincaré suggested that one should consider a pointwise mapping of a normal section across the periods. In this context arose a theory of normal forms of pointwise mappings, which is parallel to the corresponding theory for systems (1). For other generalizations of normal forms see [3], , [12]–[14].
is a fixed point. Poincaré suggested that one should consider a pointwise mapping of a normal section across the periods. In this context arose a theory of normal forms of pointwise mappings, which is parallel to the corresponding theory for systems (1). For other generalizations of normal forms see [3], , [12]–[14].
References
| [1] | H. Poincaré, "Thèse, 1928" , Oeuvres , 1 , Gauthier-Villars (1951) pp. IL-CXXXII |
| [2a] | A.D. [A.D. Bryuno] Bruno, "Analytical form of differential equations" Trans. Moscow Math. Soc. , 25 (1971) pp. 131–288 Trudy Moskov. Mat. Obshch. , 25 (1971) pp. 119–262 |
| [2b] | A.D. [A.D. Bryuno] Bruno, "Analytical form of differential equations" Trans. Moscow Math. Soc. (1972) pp. 199–239 Trudy Moskov. Mat. Obshch. , 26 (1972) pp. 199–239 |
| [3] | A.D. Bryuno, "Local methods in nonlinear differential equations" , 1 , Springer (1989) (Translated from Russian) MR0993771 |
| [4] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) MR0658490 Zbl 0476.34002 |
| [5a] | V.S. Samovol, "Linearization of a system of differential equations in the neighbourhood of a singular point" Soviet Math. Dokl. , 13 (1972) pp. 1255–1259 Dokl. Akad. Nauk SSSR , 206 (1972) pp. 545–548 Zbl 0667.34041 |
| [5b] | V.S. Samovol, "Equivalence of systems of differential equations in the neighbourhood of a singular point" Trans. Moscow Math. Soc. (2) , 44 (1982) pp. 217–237 Trudy Moskov. Mat. Obshch. , 44 (1982) pp. 213–234 |
| [6a] | G.R. Belitskii, "Equivalence and normal forms of germs of smooth mappings" Russian Math. Surveys , 33 : 1 (1978) pp. 95–155 Uspekhi Mat. Nauk. , 33 : 1 (1978) MR0490708 |
| [6b] | G.R. Belitskii, "Normal forms relative to a filtering action of a group" Trans. Moscow Math. Soc. , 40 (1979) pp. 3–46 Trudy Moskov. Mat. Obshch. , 40 (1979) pp. 3–46 |
| [6c] | G.R. Belitskii, "Smooth equivalence of germs of vector fields with a single zero eigenvalue or a pair of purely imaginary eigenvalues" Funct. Anal. Appl. , 20 : 4 (1986) pp. 253–259 Funkts. Anal. i Prilozen. , 20 : 4 (1986) pp. 1–8 |
| [7] | A.M. [A.M. Lyapunov] Liapunoff, "Problème général de la stabilité du mouvement" , Princeton Univ. Press (1947) (Translated from Russian) |
| [8] | A.L. Kunitsyn, A.P. Markev, "Stability in resonant cases" Itogi Nauk. i Tekhn. Ser. Obsh. Mekh. , 4 (1979) pp. 58–139 (In Russian) |
| [9] | J.N. Bibikov, "Local theory of nonlinear analytic ordinary differential equations" , Springer (1979) MR0547669 Zbl 0404.34005 |
| [10] | N.N. Bogolyubov, Yu.A. Mitropol'skii, "Asymptotic methods in the theory of non-linear oscillations" , Hindushtan Publ. Comp. , Delhi (1961) (Translated from Russian) MR0100379 Zbl 0151.12201 |
| [11] | A.D. [A.D. Bryuno] Bruno, "Normal form in perturbation theory" , Proc. VIII Internat. Conf. Nonlinear Oscillations, Prague, 1978 , 1 , Academia (1979) pp. 177–182 (In Russian) |
| [12] | V.V. Kostin, Le Dinh Thuy, "Some tests of the convergence of a normalizing transformation" Dapovidi Akad. Nauk URSR Ser. A : 11 (1975) pp. 982–985 (In Russian) MR407356 |
| [13] | E.J. Zehnder, "C.L. Siegel's linearization theorem in infinite dimensions" Manuscr. Math. , 23 (1978) pp. 363–371 MR0501144 Zbl 0374.47037 |
| [14] | N.V. Nikolenko, "The method of Poincaré normal forms in problems of integrability of equations of evolution type" Russian Math. Surveys , 41 : 5 (1986) pp. 63–114 Uspekhi Mat. Nauk , 41 : 5 (1986) pp. 109–152 MR0878327 Zbl 0632.35026 |
A.D. Bryuno
Comments
For more on various linearization theorems for ordinary differential equations and canonical form theorems for ordinary differential equations, as well as generalizations to the case of non-linear representations of nilpotent Lie algebras, cf. also Poincaré–Dulac theorem and Analytic theory of differential equations, and [a1].
References
| [a1] | V.I. Arnol'd, "Geometrical methods in the theory of ordinary differential equations" , Springer (1983) (Translated from Russian) |
Normal form (for matrices). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_form_(for_matrices)&oldid=24779