Normal
to a curve (or surface) at a point of it
A straight line passing through the point and perpendicular to the tangent (or tangent plane) of the curve (or surface) at this point. A smooth plane curve has at every point a unique normal situated in the plane of the curve. If a curve in a plane is given in rectangular coordinates by an equation 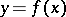 , then the equation of the normal to the curve at
, then the equation of the normal to the curve at 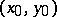 has the form
has the form
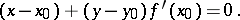 |
A curve in space has infinitely many normals at every point of it. These fill a certain plane (the normal plane). The normal lying in the osculating plane is called the principal normal; the one perpendicular to the osculating plane is called the binormal.
The normal at  to a surface given by an equation
to a surface given by an equation 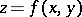 is defined by
is defined by
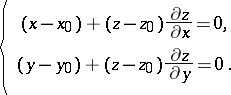 |
If the equation of the surface has the form  , then the parametric representation of the normal is
, then the parametric representation of the normal is
 |
Comments
The notion of a normal obviously extends to 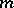 -dimensional submanifolds of Euclidean
-dimensional submanifolds of Euclidean  -space
-space  , giving an
, giving an 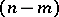 -dimensional affine subspace as the normal
-dimensional affine subspace as the normal 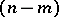 -plane to the manifold at the corresponding point. For submanifolds of (pseudo-) Riemannian manifolds, the normal planes are considered as subspaces of the tangent space of the ambient space, where orthogonality is defined by means of the (ambient) (pseudo-) Riemannian metric. See also Normal bundle; Normal plane; Normal space (to a surface).
-plane to the manifold at the corresponding point. For submanifolds of (pseudo-) Riemannian manifolds, the normal planes are considered as subspaces of the tangent space of the ambient space, where orthogonality is defined by means of the (ambient) (pseudo-) Riemannian metric. See also Normal bundle; Normal plane; Normal space (to a surface).
References
| [a1] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
| [a2] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1963) |
| [a3] | M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) pp. 145 |
| [a4] | M. Spivak, "A comprehensive introduction to differential geometry" , 1979 , Publish or Perish pp. 1–5 |
| [a5] | W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973) |
| [a6] | B.-Y. Chen, "Geometry of submanifolds" , M. Dekker (1973) |
Normal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal&oldid=11310