Norm on a field

A mapping  from
from  to the set
to the set  of real numbers, which satisfies the following conditions:
of real numbers, which satisfies the following conditions:
1)  , and
, and  if and only if
if and only if  ;
;
2)  ;
;
3)  .
.
Hence 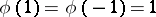 ;
; 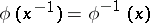 .
.
The norm of  is often denoted by
is often denoted by 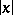 instead of
instead of 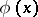 . A norm is also called an absolute value or a multiplicative valuation. Norms may (more generally) be considered on any ring with values in a linearly ordered ring [4]. See also Valuation.
. A norm is also called an absolute value or a multiplicative valuation. Norms may (more generally) be considered on any ring with values in a linearly ordered ring [4]. See also Valuation.
Examples of norms. If 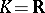 , the field of real numbers, then
, the field of real numbers, then 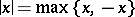 , the ordinary absolute value or modulus of the number
, the ordinary absolute value or modulus of the number 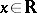 , is a norm. Similarly, if
, is a norm. Similarly, if 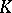 is the field
is the field  of complex numbers or the skew-field
of complex numbers or the skew-field  of quaternions, then
of quaternions, then 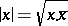 is a norm. The subfields of these fields are thus also provided with an induced norm. Any field has the trivial norm:
is a norm. The subfields of these fields are thus also provided with an induced norm. Any field has the trivial norm:
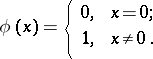 |
Finite fields and their algebraic extensions only have the trivial norm.
Examples of norms of another type are provided by logarithmic valuations of a field  : If
: If  is a valuation on
is a valuation on  with values in the group
with values in the group  and if
and if  is a real number,
is a real number, 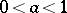 , then
, then 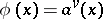 is a norm. For example, if
is a norm. For example, if 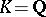 and
and  is the
is the 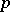 -adic valuation of the field
-adic valuation of the field  , then
, then  is called the
is called the 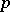 -adic absolute value or the
-adic absolute value or the 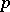 -adic norm. These absolute values satisfy the following condition, which is stronger than 3):
-adic norm. These absolute values satisfy the following condition, which is stronger than 3):
4) 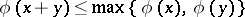 .
.
Norms satisfying condition 4) are known as ultra-metric norms or non-Archimedean norms (as distinct from Archimedean norms which do not satisfy this condition (but do satisfy 3)). They are distinguished by the fact that 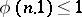 for all integers
for all integers  . All norms on a field of characteristic
. All norms on a field of characteristic 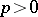 are ultra-metric. All ultra-metric norms are obtained from valuations as indicated above:
are ultra-metric. All ultra-metric norms are obtained from valuations as indicated above: 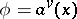 (and conversely,
(and conversely, 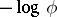 can always be taken as a valuation).
can always be taken as a valuation).
A norm 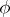 defines a metric on
defines a metric on 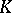 if
if 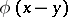 is taken as the distance between
is taken as the distance between  and
and 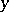 , and in this way it defines a topology on
, and in this way it defines a topology on  . The topology of any locally compact field is defined by some norm. Two norms
. The topology of any locally compact field is defined by some norm. Two norms  and
and 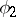 are said to be equivalent if they define the same topology; in a such case there exists a
are said to be equivalent if they define the same topology; in a such case there exists a  such that
such that  for all
for all 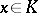 .
.
The structure of all Archimedean norms is given by Ostrowski's theorem: If 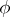 is an Archimedean norm on a field
is an Archimedean norm on a field 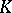 , then there exists an isomorphism of
, then there exists an isomorphism of 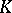 into a certain everywhere-dense subfield of one of the fields
into a certain everywhere-dense subfield of one of the fields 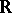 ,
, 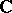 or
or  such that
such that 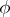 is equivalent to the norm induced by that of
is equivalent to the norm induced by that of 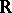 ,
, 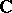 or
or  .
.
Any non-trivial norm of the field 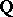 of rational numbers is equivalent either to a
of rational numbers is equivalent either to a 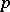 -adic norm
-adic norm 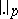 , where
, where  is a prime number, or to the ordinary norm. For any rational number
is a prime number, or to the ordinary norm. For any rational number 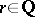 one has
one has
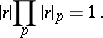 |
A similar formula is also valid for algebraic number fields [2], [3].
If 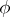 is a norm on a field
is a norm on a field 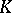 , then
, then 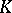 may be imbedded by the classical completion process in a field
may be imbedded by the classical completion process in a field 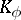 that is complete with respect to the norm that (uniquely) extends
that is complete with respect to the norm that (uniquely) extends  (cf. Complete topological space). One of the principal modern methods in the study of fields is the imbedding of a field
(cf. Complete topological space). One of the principal modern methods in the study of fields is the imbedding of a field 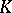 into the direct product
into the direct product 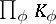 of all completions
of all completions 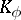 of the field
of the field 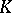 with respect to all non-trivial norms of
with respect to all non-trivial norms of  (see Adèle). If
(see Adèle). If 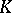 admits non-trivial valuations, then it is dense in
admits non-trivial valuations, then it is dense in 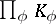 in the adèlic topology; in fact, if
in the adèlic topology; in fact, if 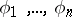 are non-trivial, non-equivalent norms on
are non-trivial, non-equivalent norms on 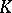 , if
, if  are elements of
are elements of 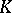 and if
and if 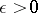 , then there exists an
, then there exists an 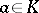 such that
such that 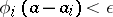 for all
for all 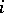 (the approximation theorem for norms).
(the approximation theorem for norms).
A norm on a field 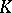 may be extended (in general, non-uniquely) to any algebraic field extension of the field
may be extended (in general, non-uniquely) to any algebraic field extension of the field 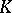 . If
. If  is complete with respect to the norm
is complete with respect to the norm 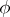 and if
and if 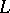 is an extension of
is an extension of  of degree
of degree  , the extension of
, the extension of 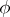 to
to 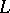 is unique, and is given by the formula
is unique, and is given by the formula
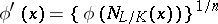 |
for 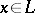 .
.
References
| [1] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
| [2] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) |
| [3] | S. Lang, "Algebra" , Addison-Wesley (1984) |
| [4] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
| [5] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986) |
Comments
Non-Archimedean norms satisfy 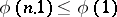 and hence do not satisfy the Archimedean axiom, whence the appellation.
and hence do not satisfy the Archimedean axiom, whence the appellation.
Norm on a field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Norm_on_a_field&oldid=16545