Natural transformation in differential geometry
The classical theory of differential-geometric objects was revisited from the functorial point of view by A. Nijenhuis, [a3]. He defined a natural bundle  over
over  -dimensional manifolds as a functor transforming every
-dimensional manifolds as a functor transforming every  -dimensional manifold
-dimensional manifold  into a fibred manifold
into a fibred manifold  over
over  (cf. Fibred space) and every local diffeomorphism
(cf. Fibred space) and every local diffeomorphism  into a fibred manifold morphism
into a fibred manifold morphism  over
over  . Later it was taken into consideration that certain geometric objects can be constructed on certain special types of manifolds only. This led to an analogous concept of bundle functor on a category over manifolds, [a1].
. Later it was taken into consideration that certain geometric objects can be constructed on certain special types of manifolds only. This led to an analogous concept of bundle functor on a category over manifolds, [a1].
From this point of view, a geometric construction on the elements of one bundle of a functor 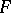 with values in the bundle of another functor
with values in the bundle of another functor  over the same base has the form of a natural transformation
over the same base has the form of a natural transformation 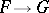 . Moreover, the
. Moreover, the 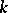 th order natural operators of
th order natural operators of  into
into 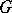 (cf. Natural operator in differential geometry) are in bijection with the natural transformations of the bundle functor of the
(cf. Natural operator in differential geometry) are in bijection with the natural transformations of the bundle functor of the 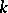 th jet prolongation
th jet prolongation  into
into 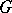 .
.
In the simplest case, if 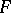 and
and  are two
are two  th order natural bundles over
th order natural bundles over 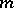 -dimensional manifolds, the natural transformations
-dimensional manifolds, the natural transformations  are in bijection with the
are in bijection with the  -equivariant mappings between their standard fibres, where
-equivariant mappings between their standard fibres, where 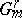 is the jet group of order
is the jet group of order  in dimension
in dimension 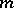 . Several methods for finding
. Several methods for finding 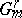 -equivariant mappings in the
-equivariant mappings in the 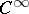 -case are collected in [a1]. If manifolds with an additional structure are studied, one has to consider the corresponding subgroup of
-case are collected in [a1]. If manifolds with an additional structure are studied, one has to consider the corresponding subgroup of  .
.
Many problems on finding natural transformations between geometrically interesting pairs of bundle functors are solved in [a1]. Even a negative answer can be of geometric interest. For example, in [a1] it is deduced that there is no natural equivalence between the iterated tangent functor 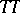 and the composition
and the composition  of the cotangent and the tangent functors. This implies that, unlike for the cotangent bundle
of the cotangent and the tangent functors. This implies that, unlike for the cotangent bundle  , there is no natural symplectic structure on the tangent bundle
, there is no natural symplectic structure on the tangent bundle  of a manifold
of a manifold 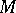 .
.
The complete description of all natural transformations between two product-preserving bundle functors 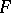 and
and  on the category of all manifolds and all
on the category of all manifolds and all  -mappings was deduced in the framework of the theory of bundle functors determined by local algebras, which was established by A. Weil, [a4] (cf. also Weil algebra). Each
-mappings was deduced in the framework of the theory of bundle functors determined by local algebras, which was established by A. Weil, [a4] (cf. also Weil algebra). Each 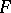 or
or  corresponds to a local algebra
corresponds to a local algebra  or
or 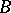 , respectively, and all natural transformations
, respectively, and all natural transformations 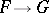 are in bijection with the algebra homomorphisms
are in bijection with the algebra homomorphisms 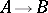 , see [a1] for a survey. An analogous characterization of all natural transformations between two product preserving bundle functors on the category of fibred manifolds was deduced by W. Mikulski, [a2].
, see [a1] for a survey. An analogous characterization of all natural transformations between two product preserving bundle functors on the category of fibred manifolds was deduced by W. Mikulski, [a2].
References
| [a1] | I. Kolář, P.W. Michor, J. Slovák, "Natural operations in differential geometry" , Springer (1993) |
| [a2] | W. Mikulski, "Product preserving bundle functors on fibered manifolds" Archivum Math. (Brno) , 32 (1996) pp. 307–316 |
| [a3] | A. Nijenhuis, "Natural bundles and their general properties" , Diff. Geom. in Honor of K. Yano , Kinokuniya (1972) pp. 317–334 |
| [a4] | A. Weil, "Théorie des points proches sur les variétés différentiables" Colloq. C.N.R.S., Strasbourg (1953) pp. 111–117 |
Natural transformation in differential geometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Natural_transformation_in_differential_geometry&oldid=13906