Multiplication of distributions
multiplication of generalized functions
Let  be an open subset of
be an open subset of  . Following L. Schwartz [a7], a distribution, or generalized function,
. Following L. Schwartz [a7], a distribution, or generalized function,  can be multiplied by a smooth function
can be multiplied by a smooth function  , the result being defined by its action on a test function
, the result being defined by its action on a test function  :
: 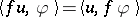 . The example of
. The example of
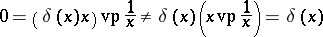 |
shows that this product is not associative (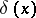 denotes the Dirac measure,
denotes the Dirac measure,  the principal value distribution, cf. Generalized function; Generalized functions, product of). There are further limitations on defining products of distributions. Schwartz [a6] proved that whenever an associative differential algebra
the principal value distribution, cf. Generalized function; Generalized functions, product of). There are further limitations on defining products of distributions. Schwartz [a6] proved that whenever an associative differential algebra 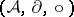 contains
contains 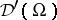 , the operations
, the operations 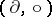 in
in 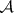 cannot simultaneously be faithful extensions of the distributional derivatives and the pointwise product of continuous functions. Thus, a multiplication of distributions can either be defined by imbedding the space of distributions into algebras, but giving up one or the other of the consistency properties above, or else can be defined only on subspaces of
cannot simultaneously be faithful extensions of the distributional derivatives and the pointwise product of continuous functions. Thus, a multiplication of distributions can either be defined by imbedding the space of distributions into algebras, but giving up one or the other of the consistency properties above, or else can be defined only on subspaces of 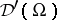 or for certain individual distributions.
or for certain individual distributions.
The first approach is summarized under the heading generalized function algebras. By common usage of the term, "multiplication of distributions" refers to the second approach. Here again one may distinguish multiplier theory (multiplication as a continuous bilinear mapping on linear topological subspaces of 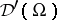 ) and methods producing individual distributional products (without continuity at large of the operations).
) and methods producing individual distributional products (without continuity at large of the operations).
Multiplier theory.
Typical examples are provided by the continuous multiplication mapping on the spaces of integration theory  ,
,  , or the Sobolov spaces
, or the Sobolov spaces 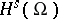 (cf. also Sobolev classes (of functions)), which form an algebra when
(cf. also Sobolev classes (of functions)), which form an algebra when 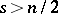 . By duality, a multiplication mapping
. By duality, a multiplication mapping  can be defined. For multiplier theory in Sobolev–Besov spaces, see [a8].
can be defined. For multiplier theory in Sobolev–Besov spaces, see [a8].
Another example arises from the convolution algebra 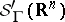 of tempered distributions with support in an acute cone
of tempered distributions with support in an acute cone 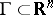 . The inverse image of
. The inverse image of 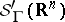 under the Fourier transform
under the Fourier transform 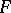 is the algebra of retarded distributions, on which the product, defined by
is the algebra of retarded distributions, on which the product, defined by 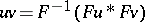 , is a sequentially continuous bilinear mapping.
, is a sequentially continuous bilinear mapping.
Individual distributional products.
Product mappings will be defined on certain subsets 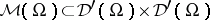 with values in
with values in 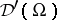 . The product will be bilinear, when applicable, commutative and partially associative: If
. The product will be bilinear, when applicable, commutative and partially associative: If  and
and 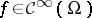 , then both
, then both 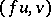 and
and 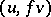 belong to
belong to 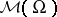 and
and 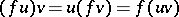 . With these properties, localization is possible, that is, the product mapping is uniquely defined by its restrictions to open neighbourhoods of points in
. With these properties, localization is possible, that is, the product mapping is uniquely defined by its restrictions to open neighbourhoods of points in  . Equivalently, it suffices to define the products
. Equivalently, it suffices to define the products 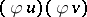 for every
for every  to specify
to specify 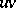 . The following definitions are instances of such products of increasing generality.
. The following definitions are instances of such products of increasing generality.
a) 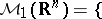 pairs of distributions with disjoint singular support
pairs of distributions with disjoint singular support . This is the localized version of the product of a distribution and a smooth function. Note that
. This is the localized version of the product of a distribution and a smooth function. Note that 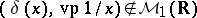 .
.
b) 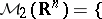 pairs of distributions
pairs of distributions 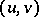 such that the
such that the 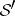 -convolution of
-convolution of 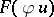 and
and 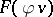 exists for all
exists for all 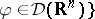 . The definition of the
. The definition of the 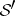 -convolution is a generalization of the convolution in
-convolution is a generalization of the convolution in 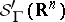 not requiring the support property, see [a3]. The product is defined locally by
not requiring the support property, see [a3]. The product is defined locally by 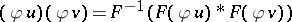 . The product of retarded distributions is a special case, as is the wave front set criterion of L. Hörmander [a4] (cf. also Wave front): If for all
. The product of retarded distributions is a special case, as is the wave front set criterion of L. Hörmander [a4] (cf. also Wave front): If for all 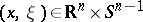 ,
,  implies
implies 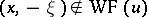 , then
, then 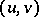 belongs to
belongs to 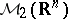 .
.
c) Regularization and passage to the limit. A strict delta-net is a net (cf. also Net (directed set)) of test functions 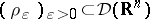 such that the supports of the functions
such that the supports of the functions 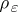 shrink to
shrink to 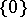 as
as 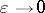 ,
, 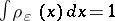 and
and 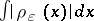 is bounded independently of
is bounded independently of  . A model delta-net is a net of the form
. A model delta-net is a net of the form 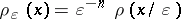 with
with 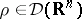 fixed. Then
fixed. Then
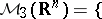 pairs of distributions
pairs of distributions 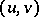 such that
such that  exists for all strict delta-nets
exists for all strict delta-nets 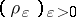 and
and 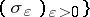 ;
;
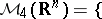 pairs of distributions
pairs of distributions 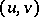 such that
such that 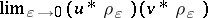 exists for all model delta nets
exists for all model delta nets 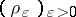 and does not depend on the net chosen
and does not depend on the net chosen . The product of
. The product of  and
and  is defined by the respective limit. Various other classes of delta nets are in use as well.
is defined by the respective limit. Various other classes of delta nets are in use as well.
d) Harmonic regularization. Every distribution 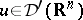 can be represented as the boundary value as
can be represented as the boundary value as 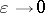 of a harmonic function
of a harmonic function 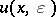 in the variables
in the variables 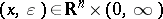 , obtained by convolution with the Poisson kernel (locally; cf. also Poisson integral). Then
, obtained by convolution with the Poisson kernel (locally; cf. also Poisson integral). Then
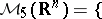 pairs of distributions
pairs of distributions  such that
such that 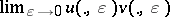 exists
exists . The product by analytic regularization in dimension
. The product by analytic regularization in dimension 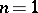 is a special case.
is a special case.
It holds that 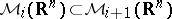 for all
for all 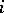 , and the products coincide when they exist, see [a1], [a5]. Every inclusion is strict. The products defined in multiplier theory are special cases of
, and the products coincide when they exist, see [a1], [a5]. Every inclusion is strict. The products defined in multiplier theory are special cases of 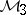 . A short review of further definitions, which may produce results not consistent with
. A short review of further definitions, which may produce results not consistent with 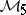 , can be found in [a5].
, can be found in [a5].
The products 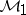 –
–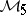 can be used to define restrictions of distributions to submanifolds or to compute convolutions, for example. Generally (with exceptions), they cannot be used to define multiplications arising in non-linear partial differential equations because they are not stable with respect to perturbations, due to lack of continuity. In non-linear partial differential equations, either generalized function algebras or multiplier theory are applicable. A typical example for the latter is a conservation law like
can be used to define restrictions of distributions to submanifolds or to compute convolutions, for example. Generally (with exceptions), they cannot be used to define multiplications arising in non-linear partial differential equations because they are not stable with respect to perturbations, due to lack of continuity. In non-linear partial differential equations, either generalized function algebras or multiplier theory are applicable. A typical example for the latter is a conservation law like 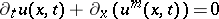 where the multiplication is done in
where the multiplication is done in 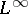 and the derivatives are computed in
and the derivatives are computed in 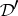 .
.
Related to multiplier theory, introduced to derive estimates in non-linear (pseudo-)differential equations, is the paraproduct of J.M. Bony [a2]. Given 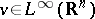 with compact support, the paramultiplication by
with compact support, the paramultiplication by  is a linear operator
is a linear operator 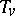 mapping the Sobolev space
mapping the Sobolev space 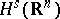 into itself for any
into itself for any 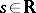 . The paraproduct does not reproduce the pointwise product (when defined by multiplier theory, for example) but serves to control non-linear terms up to some more regular deviation. For example, if
. The paraproduct does not reproduce the pointwise product (when defined by multiplier theory, for example) but serves to control non-linear terms up to some more regular deviation. For example, if  ,
,  belong to
belong to  with
with 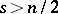 , then
, then 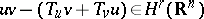 for every
for every 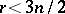 .
.
See also Generalized function algebras.
References
| [a1] | V. Boie, "Multiplication of distributions" Comment. Math. Univ. Carolinae , 39 (1998) pp. 309–321 |
| [a2] | J.M. Bony, "Calcul symbolique et propagation des singularités pour les équations aux dérivées partielles non linéaires" Ann. Sci. École Norm. Sup. Sér. 4 , 14 (1981) pp. 209–246 |
| [a3] | P. Dierolf, J. Voigt, "Convolution and 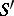 -convolution of distributions" Collect. Math. , 29 (1978) pp. 185–196 -convolution of distributions" Collect. Math. , 29 (1978) pp. 185–196 |
| [a4] | L. Hörmander, "Fourier integral operators I" Acta Math. , 127 (1971) pp. 79–183 |
| [a5] | M. Oberguggenberger, "Multiplication of distributions and applications to partial differential equations" , Longman (1992) |
| [a6] | L. Schwartz, "Sur l'impossibilité de la multiplication des distributions" C.R. Acad. Sci. Paris , 239 (1954) pp. 847–848 |
| [a7] | L. Schwartz, "Théorie des distributions" , Hermann (1966) (Edition: nouvelle) |
| [a8] | H. Triebel, "Theory of function spaces" , Birkhäuser (1983) |
Multiplication of distributions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multiplication_of_distributions&oldid=16743