Multilinear form
 -linear form, on a unitary
-linear form, on a unitary  -module
-module 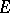
A multilinear mapping 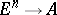 (here
(here 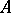 is a commutative associative ring with a unit, cf. Associative rings and algebras). A multilinear form is also called a multilinear function (
is a commutative associative ring with a unit, cf. Associative rings and algebras). A multilinear form is also called a multilinear function ( -linear function). Since a multilinear form is a particular case of a multilinear mapping, one can speak of symmetric, skew-symmetric, alternating, symmetrized, and skew-symmetrized multilinear forms. For example, the determinant of a square matrix of order
-linear function). Since a multilinear form is a particular case of a multilinear mapping, one can speak of symmetric, skew-symmetric, alternating, symmetrized, and skew-symmetrized multilinear forms. For example, the determinant of a square matrix of order  over
over 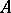 is a skew-symmetrized (and therefore alternating)
is a skew-symmetrized (and therefore alternating)  -linear form on
-linear form on 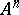 . The
. The  -linear forms on
-linear forms on 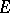 form an
form an 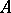 module
module 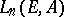 , which is naturally isomorphic to the module
, which is naturally isomorphic to the module 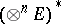 of all linear forms on
of all linear forms on 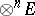 . In the case
. In the case 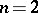 (
(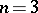 ), one speaks of bilinear forms (cf. Bilinear form) (respectively, trilinear forms).
), one speaks of bilinear forms (cf. Bilinear form) (respectively, trilinear forms).
The  -linear forms on
-linear forms on  are closely related to
are closely related to  -times covariant tensors, i.e. elements of the module
-times covariant tensors, i.e. elements of the module  . More precisely, there is a linear mapping
. More precisely, there is a linear mapping
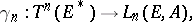 |
such that
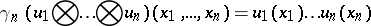 |
for any  ,
, 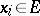 . If the module
. If the module 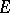 is free (cf. Free module),
is free (cf. Free module), 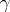 is injective, while if
is injective, while if 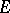 is also finitely generated,
is also finitely generated, 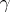 is bijective. In particular, the
is bijective. In particular, the  -linear forms on a finite-dimensional vector space over a field are identified with
-linear forms on a finite-dimensional vector space over a field are identified with  -times covariant tensors.
-times covariant tensors.
For any forms 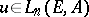 ,
,  one can define the tensor product
one can define the tensor product 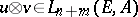 via the formula
via the formula
 |
For symmetrized multilinear forms (cf. Multilinear mapping), a symmetrical product is also defined:
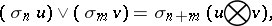 |
while for skew-symmetrized multilinear forms there is an exterior product
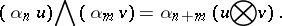 |
These operations are extended to the module  , where
, where 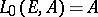 ,
, 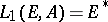 , to the module of symmetrized forms
, to the module of symmetrized forms 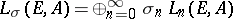 and to the module of skew-symmetrized forms
and to the module of skew-symmetrized forms 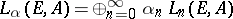 respectively, which transforms them into associative algebras with a unit. If
respectively, which transforms them into associative algebras with a unit. If 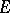 is a finitely-generated free module, then the mappings
is a finitely-generated free module, then the mappings 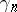 define an isomorphism of the tensor algebra
define an isomorphism of the tensor algebra  on
on 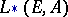 and the exterior algebra
and the exterior algebra 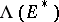 on the algebra
on the algebra 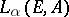 , which in that case coincides with the algebra of alternating forms. If
, which in that case coincides with the algebra of alternating forms. If 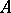 is a field of characteristic
is a field of characteristic  , then there is also an isomorphism of the symmetric algebra
, then there is also an isomorphism of the symmetric algebra  on the algebra
on the algebra 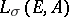 of symmetric forms.
of symmetric forms.
Any multilinear form 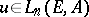 corresponds to a function
corresponds to a function 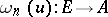 , given by the formula
, given by the formula
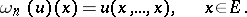 |
Functions of the form 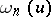 are called forms of degree
are called forms of degree  on
on 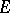 ; if
; if 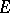 is a free module, then in coordinates relative to an arbitrary basis they are given by homogeneous polynomials of degree
is a free module, then in coordinates relative to an arbitrary basis they are given by homogeneous polynomials of degree  . In the case
. In the case 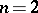 (
( ) one obtains quadratic (cubic) forms on
) one obtains quadratic (cubic) forms on 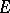 (cf. Quadratic form; Cubic form). The form
(cf. Quadratic form; Cubic form). The form 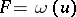 completely determines the symmetrization
completely determines the symmetrization 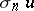 of a form
of a form 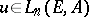 :
:
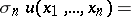 |
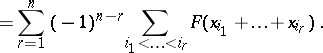 |
In particular, for 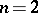 ,
,
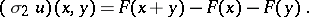 |
The mappings 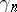 and
and 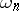 define a homomorphism of the algebra
define a homomorphism of the algebra 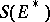 on the algebra of all polynomial functions (cf. Polynomial function)
on the algebra of all polynomial functions (cf. Polynomial function) 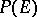 , which is an isomorphism if
, which is an isomorphism if 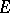 is a finitely-generated free module over an infinite integral domain
is a finitely-generated free module over an infinite integral domain 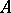 .
.
References
| [1] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) |
| [2] | N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French) |
| [3] | S. Lang, "Algebra" , Addison-Wesley (1984) |
Multilinear form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multilinear_form&oldid=16677