Monge-Ampère equation
A second-order partial differential equation of the form
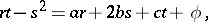 |
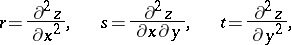 |
with coefficients depending on variables  ,
, 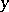 , the unknown function
, the unknown function 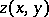 , and its first derivatives
, and its first derivatives
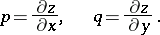 |
The type of a Monge–Ampère equation depends on the sign of the expression
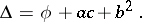 |
If  , then the Monge–Ampère equation is of elliptic type, if
, then the Monge–Ampère equation is of elliptic type, if 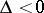 it is of hyperbolic type and if
it is of hyperbolic type and if  it is of parabolic type. A Monge–Ampère equation is invariant under contact transformations (cf. Contact transformation). In particular, the transformation
it is of parabolic type. A Monge–Ampère equation is invariant under contact transformations (cf. Contact transformation). In particular, the transformation
 |
transforms the equation
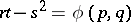 |
into the equation
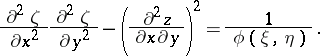 |
The development of the theory of Monge–Ampère equations is mainly connected with the solution of various geometric problems which, when formulated analytically, reduce to the discussion of such equations. For example, the construction of a surface with a given line element reduces to the solution of the Darboux equation, which is a Monge–Ampère equation. In the case of a semi-geodesic parametrization (with line element 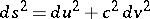 ) this equation takes the form
) this equation takes the form
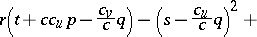 |
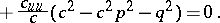 |
The type of the Darboux equation depends on the sign of the Gaussian curvature 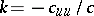 . For a hyperbolic Darboux equation (negative Gaussian curvature) the characteristics are asymptotic lines. An application of the Cauchy–Kovalevskaya theorem to Darboux's equation gives a theorem about the existence of a surface with a given line element whose coefficients are analytic functions.
. For a hyperbolic Darboux equation (negative Gaussian curvature) the characteristics are asymptotic lines. An application of the Cauchy–Kovalevskaya theorem to Darboux's equation gives a theorem about the existence of a surface with a given line element whose coefficients are analytic functions.
The particularly high level of development of the theory of elliptic Monge–Ampère equations is due to the introduction of the idea of a generalized solution and the application of geometric methods for their solution. In the simplest case of the equation 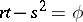 , a generalized solution is defined as a convex function
, a generalized solution is defined as a convex function 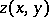 satisfying the equality
satisfying the equality
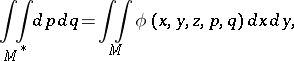 |
where 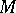 is an arbitrary Borel set in the
is an arbitrary Borel set in the 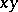 -plane in the domain in which the solution is to be discussed, and
-plane in the domain in which the solution is to be discussed, and 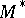 is the so-called normal image of
is the so-called normal image of 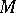 , which consists of those points of the
, which consists of those points of the 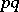 -plane for which
-plane for which 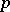 and
and 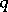 are the angular coefficients of the support planes to the surface
are the angular coefficients of the support planes to the surface 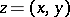 at points
at points 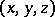 projecting into
projecting into 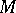 . A regular (twice-differentiable) solution is also a generalized solution. A generalized solution in the case that
. A regular (twice-differentiable) solution is also a generalized solution. A generalized solution in the case that 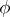 is a continuous positive function is smooth; however, the second derivatives need not exist. The construction of a generalized solution essentially reduces to the purely geometric problem of constructing an infinite convex polyhedron with given directions for the finite faces and given functions on these faces. In particular, if the right-hand side
is a continuous positive function is smooth; however, the second derivatives need not exist. The construction of a generalized solution essentially reduces to the purely geometric problem of constructing an infinite convex polyhedron with given directions for the finite faces and given functions on these faces. In particular, if the right-hand side 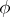 of the equation depends only on
of the equation depends only on  and
and 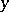 , then this function is the area of the face. Passage to the limit of these polyhedra gives the graph of a generalized solution of the equation. For generalized solutions fairly general existence and uniqueness theorems have been obtained for the solution of the Dirichlet problem. In particular, there is the following theorem. The Dirichlet problem for the equation
, then this function is the area of the face. Passage to the limit of these polyhedra gives the graph of a generalized solution of the equation. For generalized solutions fairly general existence and uniqueness theorems have been obtained for the solution of the Dirichlet problem. In particular, there is the following theorem. The Dirichlet problem for the equation
 |
in a convex domain  is solvable for any continuous boundary values if the curvature of the curve bounding
is solvable for any continuous boundary values if the curvature of the curve bounding 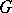 is positive, if
is positive, if 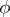 is continuous, positive, non-decreasing in
is continuous, positive, non-decreasing in  , and, as
, and, as 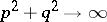 , has order of growth not exceeding
, has order of growth not exceeding 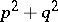 . For a given direction of convexity this solution is unique.
. For a given direction of convexity this solution is unique.
An essential result in the theory of elliptic Monge–Ampère equations is the theorem on regularity of generalized solutions. For the simplest equation
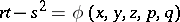 |
this theorem reads: For 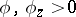 every generalized solution with a regular right-hand side
every generalized solution with a regular right-hand side 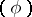 is regular. Namely, if
is regular. Namely, if 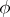 is
is 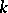 times differentiable
times differentiable 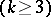 , then the generalized solution is
, then the generalized solution is 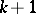 times differentiable. If
times differentiable. If 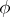 is analytic, then the generalized solution is analytic.
is analytic, then the generalized solution is analytic.
Among the general elliptic Monge–Ampère equations the strongly-elliptic Monge–Ampère equations are the ones most studied. These are the equations for which 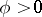 and the quadratic form
and the quadratic form
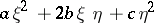 |
is non-negative. The basic results, quoted above for the simplest Monge–Ampère equations, have been extended to the strongly-elliptic case. The idea of a generalized solution has been introduced, and under very general conditions the existence and uniqueness of the solution to the Dirichlet problem as well as regularity of a generalized solution, depending on the regularity of the coefficients of the equation, has been proved. Darboux's equation for a line element with positive curvature is, in general, not strongly elliptic. A generalized solution for it is defined as the  -coordinate of a surface realizing the given line element. Darboux's equation has a generalized solution in any domain that is convex in the sense of the given metric (the geodesic curvature of the boundary should be positive). In any such domain, under sufficiently general conditions, the solvability of the Dirichlet problem has been proved. A generalized solution is regular if the coefficients of the line element are regular. The generalized solution is analytic if the coefficients are analytic.
-coordinate of a surface realizing the given line element. Darboux's equation has a generalized solution in any domain that is convex in the sense of the given metric (the geodesic curvature of the boundary should be positive). In any such domain, under sufficiently general conditions, the solvability of the Dirichlet problem has been proved. A generalized solution is regular if the coefficients of the line element are regular. The generalized solution is analytic if the coefficients are analytic.
Important results have been obtained for elliptic Monge–Ampère equations on manifolds homeomorphic to the sphere. In particular, two classical problems reduce to such equations: the Weyl problem and the Minkowski problem. The solutions of these problems, obtained by passage to the limit over polyhedra, are generalized. Regularity of these solutions is obtained from theorems on the regularity of generalized solutions.
Monge–Ampère equations were considered by G. Monge (1784) and A. Ampère (1820).
References
| [1] | E. Goursat, "Cours d'analyse mathématique" , 3 , Gauthier-Villars (1923) pp. Part 1 |
| [2] | A.V. Pogorelov, "Monge–Ampère equations of elliptic type" , Noordhoff (1964) (Translated from Russian) |
| [3] | A.V. Pogorelov, "Extrinsic geometry of convex surfaces" , Amer. Math. Soc. (1972) (Translated from Russian) |
Comments
In 1950–1970 the study of boundary value problems for general two-dimensional Monge–Ampère equations was a most active research area.
Necessary and sufficient conditions for solvability of the Dirichlet problem and other boundary value problems were obtained for generalized and regular solutions of general two-dimensional elliptic Monge–Ampère equations. Also completely investigated was the regularity of generalized solutions for the most important classes of two-dimensional elliptic Monge–Ampère equations (the Darboux equation, equations 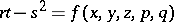 for which
for which 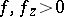 , and strongly-elliptic equations), under the condition that the prescribed data are sufficiently regular. The sharp uniqueness and non-uniqueness theorems were obtained for generalized and regular solutions of these boundary value problems. Profound applications to global problems of classical differential geometry were done on the basis of these results.
, and strongly-elliptic equations), under the condition that the prescribed data are sufficiently regular. The sharp uniqueness and non-uniqueness theorems were obtained for generalized and regular solutions of these boundary value problems. Profound applications to global problems of classical differential geometry were done on the basis of these results.
The global theorems of non-existence of regular solutions (mainly for the Darboux equation) were established for two-dimensional hyperbolic Monge–Ampère equations. A few existence theorems for regular solutions of the Cauchy problem were proved for two-dimensional hyperbolic Monge–Ampère equations. The solution of a few important global problems for saddle surfaces was obtained as an application of these results.
From 1970 up to the present time (1989) the most active research area shifts to the theory of elliptic solutions for real and complex  -dimensional Monge–Ampère equations,
-dimensional Monge–Ampère equations, 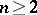 .
.
Real multi-dimensional Monge–Ampère equations.
New fundamental difficulties arise at the transition from two-dimensional Monge–Ampère equations to the multi-dimensional case. Necessary and sufficient conditions were obtained for generalized and regular elliptic solutions of  -dimensional Monge–Ampère equations,
-dimensional Monge–Ampère equations,  . Completely investigated is the regularity of certain generalized elliptic equations under the condition that the prescribed data are sufficiently regular. The sharp uniqueness and non-uniqueness theorems were obtained for generalized and regular solutions of the corresponding boundary value problems. The connections between variational problems and the Dirichlet problem for elliptic solutions of Monge–Ampère equations were also established.
. Completely investigated is the regularity of certain generalized elliptic equations under the condition that the prescribed data are sufficiently regular. The sharp uniqueness and non-uniqueness theorems were obtained for generalized and regular solutions of the corresponding boundary value problems. The connections between variational problems and the Dirichlet problem for elliptic solutions of Monge–Ampère equations were also established.
Profound applications to global problems of differential geometry, non-linear elliptic partial differential equations and the calculus of variations were obtained on the basis of these results.
Complex multi-dimensional Monge–Ampère equations.
Various important investigations were made for elliptic solutions of  -dimensional complex Monge–Ampère equations. The solvability of the Dirichlet problem for regular elliptic solutions of such equations was obtained. Deep connections with Kähler and other classical complex manifolds were established, and many interesting applications to differential geometry and topology were obtained.
-dimensional complex Monge–Ampère equations. The solvability of the Dirichlet problem for regular elliptic solutions of such equations was obtained. Deep connections with Kähler and other classical complex manifolds were established, and many interesting applications to differential geometry and topology were obtained.
References
| [a1] | L. Nirenberg, "The Weyl and Minkowski problems in differential geometry in the large" Comm. Pure Appl. Math. , 6 (1953) pp. 103–156 |
| [a2] | I.J. Bakelman, "Generalized solutions of Monge–Ampère equations" Dokl. Akad. Nauk SSSR , 114 (1957) pp. 1143–1145 (In Russian) |
| [a3] | A.D. Aleksandrov, "The Dirichlet problem for the equation 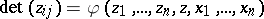 " Vestnik Leningradsk. Gosudarstv. Univ. : 1 (1958) (In Russian) " Vestnik Leningradsk. Gosudarstv. Univ. : 1 (1958) (In Russian) |
| [a4] | I.J. Bakelman, "Geometric methods for solving elliptic equations" , Moscow (1965) (In Russian) |
| [a5] | A.V. Pogorelov, "Monge–Ampère equations of elliptic type" , Noordhoff (1964) (Translated from Russian) |
| [a6] | N.V. Efimov, "The appearance of singularities on surfaces of negative curvature" Mat. Sb. , 64 : 2 (1964) pp. 286–320 (In Russian) |
| [a7] | N.V. Efimov, "Surfaces with a slowly changing negative curvature" Russian Math. Surveys , 21 : 5 (1966) pp. 1–55 Uspekhi Mat. Nauk. , 21 : 5 (1966) pp. 3–58 |
| [a8] | E.G. Poznyak, "A regular realization of two-dimensional metrics with negative curvature" Ukr. Geom. Sb. , 3 (1966) pp. 78–92 (In Russian) |
| [a9] | A.V. Pogorelov, "The Minkowski multidimensional problem" , Wiley (1978) (Translated from Russian) |
| [a10] | S. Cheng, S.T. Yau, "On the regularity of the solutions of the Monge–Ampère equations 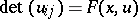 " Comm. Pure Appl. Math. , 30 (1977) pp. 41–68 " Comm. Pure Appl. Math. , 30 (1977) pp. 41–68 |
| [a11] | S.-T. Yau, "Survey on partial differential equations in differential geometry" S.-T. Yau (ed.) , Sem. Differential Geom. , Princeton Univ. Press (1982) pp. 669–706 |
| [a12] | S.T. Yau, "On the Ricci curvature of a compact Kähler manifold and the complex Monge–Ampère equation I" Comm. Pure Appl. Math. , 31 (1978) pp. 339–411 |
| [a13] | I.J. Bakelman, "Applications of the Monge–Ampère operators to the Dirichlet problem for quasilinear elliptic equations" S.-T. Yau (ed.) , Sem. Differential Geom. , Princeton Univ. Press (1982) pp. 239–258 |
| [a14] | T. Aubin, "Nonlinear analysis on manifolds. Monge–Ampère equations" , Springer (1982) |
| [a15] | I.J. Bakelman, "Variational problems and elliptic Monge–Ampére equations" J. Differential Geom. , 18 (1983) pp. 669–699 |
| [a16] | L. Caffarelli, L. Nirenberg, J. Spruck, "The Dirichlet problem for nonlinear second order elliptic equations, I: Monge–Ampère equations" Comm. Pure Appl. Math. , 37 (1984) pp. 369–402 |
| [a17] | L. Caffarelli, J.J. Kohn, L. Nirenberg, J. Sprick, "The Dirichlet problem for nonlinear second order elliptic equations, II: Complex Monge–Ampère equations and uniformly elliptic equations" Comm. Pure Appl. Math. , 38 (1985) pp. 261–301 |
| [a18] | I.J. Bakelman, "Generalized elliptic solutions of the Dirichlet problem for  -dimensional Monge–Ampère equations" F.E. Browder (ed.) , Nonlinear Functional Anal. Applic. , Proc. Symp. Pure Math. , 45.1 , Amer. Math. Soc. (1966) pp. 73–102 -dimensional Monge–Ampère equations" F.E. Browder (ed.) , Nonlinear Functional Anal. Applic. , Proc. Symp. Pure Math. , 45.1 , Amer. Math. Soc. (1966) pp. 73–102 |
| [a19] | D. Gilbarg, N.S. Trudinger, "Elliptic partial differential equations of the second order" , Springer (1984) |
| [a20] | N.V. Krylov, "Nonlinear elliptic and parabolic equations of the second order" , Kluwer (1987) (Translated from Russian) |
| [a21] | H. Minkowski, "Volumen und Oberflächen" Math. Ann. , 57 (1903) pp. 447–495 |
| [a22] | H. Weyl, "Ueber die Starrheit der Eiflächen und konvexen Flächen durch ihr Linienelement" Vierteljahrschrift naturforsch. Gesellschaft Zürich , 61 (1916) pp. 40–72 |
| [a23] | H. Lewy, "On differential geometry in the large 1" Trans. Amer. Math. Soc. , 43 (1938) pp. 258–270 |
| [a24] | E. Calabi, "Improper affine hyperspheres of convex type and a generalization of a theorem by K. Jörgens" Michigan Math. J. , 5 (1958) pp. 105–126 |
| [a25] | J. Serrin, "The Dirichlet problem for the minimal surface equation in higher dimension" J. Reine Angew. Math. , 223 (1968) pp. 170–187 |
| [a26] | I.J. Bakelman, "Geometric problems in quasilinear elliptic equations" Russian Math. Surveys , 25 : 3 (1970) pp. 45–109 Uspekhi Mat. Nauk , 25 : 3 (1970) pp. 49–112 |
| [a27] | S.Y. Cheng, S.T. Yau, "On the regularity of the solution of the  -dimensional Minkowski problem" Comm. Pure Appl. Math. , 29 (1976) pp. 495–516 -dimensional Minkowski problem" Comm. Pure Appl. Math. , 29 (1976) pp. 495–516 |
| [a28] | P.L. Lions, "Sur les équations de Monge–Ampère" Manuscripta Math. , 41 (1983) pp. 1–43 |
Monge-Ampère equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Monge-Amp%C3%A8re_equation&oldid=16131