Matsushima criterion
From Encyclopedia of Mathematics
The homogeneous space  , where
, where 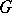 is an affine reductive algebraic group (cf. also Affine group; Reductive group) defined over an algebraically closed field
is an affine reductive algebraic group (cf. also Affine group; Reductive group) defined over an algebraically closed field 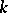 and
and 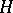 is a closed subgroup of
is a closed subgroup of 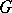 , is an affine algebraic variety if and only if
, is an affine algebraic variety if and only if 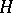 is a reductive group. This criterion was first found by Y. Matsushima [1] in the case where
is a reductive group. This criterion was first found by Y. Matsushima [1] in the case where 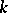 is the complex field. Later, proofs were given that are valid for every algebraically closed field of characteristic zero (see [2], [3], [4]). In the case where the characteristic of
is the complex field. Later, proofs were given that are valid for every algebraically closed field of characteristic zero (see [2], [3], [4]). In the case where the characteristic of 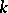 is positive, the proof of the criterion was obtained only after the proof of the Mumford hypothesis (see [5], [6]).
is positive, the proof of the criterion was obtained only after the proof of the Mumford hypothesis (see [5], [6]).
References
| [1] | Y. Matsushima, "Espaces homogènes de Stein des groupes de Lie complexes" Nagoya Math. J. , 16 (1960) pp. 205–218 |
| [2] | A. Białynicki-Birula, "On homogeneous affine spaces of linear algebraic groups" Amer. J. Math. , 85 (1963) pp. 577–582 |
| [3] | D. Luna, "Slices étales" Bull. Soc. Math. France , 33 (1973) pp. 81–105 |
| [4] | A. Borel, Harish-Chandra, "Arithmetic subgroups of algebraic groups" Ann. of Math. , 75 (1962) pp. 485–535 |
| [5] | E.A. Nisnevich, "Affine homogeneous spaces and finite subgroups of arithmetic groups over function fields" Funct. Anal. Appl. , 11 : 1 (1977) pp. 64–65 Funktsional. Anal. i Prilozhen. , 11 : 1 (1977) pp. 73–74 |
| [6] | R.W. Richardson, "Affine coset spaces of reductive algebraic groups" Bull. London Math. Soc. , 9 (1977) pp. 38–41 |
How to Cite This Entry:
Matsushima criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matsushima_criterion&oldid=19096
Matsushima criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matsushima_criterion&oldid=19096
This article was adapted from an original article by V.L. Popov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article