Lyndon word
A word is a sequence of letters  , that is, elements chosen from a set
, that is, elements chosen from a set  called an alphabet. A word is usually written as
called an alphabet. A word is usually written as  , or abbreviated by a single symbol:
, or abbreviated by a single symbol:  . The length of
. The length of  is equal to the number of letters in
is equal to the number of letters in  , i.e.
, i.e.  . One may concatenate two words
. One may concatenate two words  ,
,  , and this operation is concisely written as
, and this operation is concisely written as  . Words may be ordered lexicographically; more precisely, given a total order
. Words may be ordered lexicographically; more precisely, given a total order  on
on  , one may extend it over the set of words by setting
, one may extend it over the set of words by setting 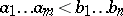 if either
if either  and
and 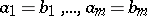 or there exists an
or there exists an  such that
such that  with
with 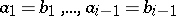 and
and 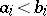 . This word order is sometimes referred to as alphabetical order. For more details, see [a1].
. This word order is sometimes referred to as alphabetical order. For more details, see [a1].
Lyndon words are words strictly less than any of their non-empty proper right factors (or strict suffixes), that is, 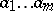 is a Lyndon word if it is strictly less than
is a Lyndon word if it is strictly less than 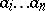 for
for  (with respect to the lexicographic order). These were introduced by R.C. Lyndon [a2] for constructing bases of the lower central series for free groups (cf. Central series of a group). From the definition one can see that letters are Lyndon words. Equivalently,
(with respect to the lexicographic order). These were introduced by R.C. Lyndon [a2] for constructing bases of the lower central series for free groups (cf. Central series of a group). From the definition one can see that letters are Lyndon words. Equivalently,  is a Lyndon word if it is strictly less than any of the circular shifts
is a Lyndon word if it is strictly less than any of the circular shifts 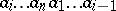 (
( ). One important characterization of these words yields a recursive process to generate them: a word
). One important characterization of these words yields a recursive process to generate them: a word 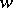 is a Lyndon word if and only if there exists two Lyndon words
is a Lyndon word if and only if there exists two Lyndon words  ,
,  such that
such that  and
and  . J.P. Duval [a3] gave a beautiful, and clever, algorithm that generates Lyndon words of bounded length over a finite alphabet. The number of Lyndon words of length
. J.P. Duval [a3] gave a beautiful, and clever, algorithm that generates Lyndon words of bounded length over a finite alphabet. The number of Lyndon words of length  over a finite alphabet of cardinality
over a finite alphabet of cardinality  may be explicitly computed, using Witt's formula:
may be explicitly computed, using Witt's formula:
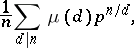 |
where  is the Möbius function.
is the Möbius function.
A multi-homogeneous version of Witt's formula may be found in [a4]. The central result about Lyndon words is the following Chen–Fox–Lyndon theorem: Any word can be expressed as a unique non-increasing product of Lyndon words. The preceding characterization suggests an algorithm to compute this factorization. Duval [a5] gave a simple and efficient algorithm that factorizes a word in linear time.
The applications of Lyndon words, in algebra and combinatorics, seem innumerable. For instance, there are as many Lyndon words over an alphabet of cardinality  (
( a prime) as there are irreducible polynomials over a finite field of characteristic
a prime) as there are irreducible polynomials over a finite field of characteristic 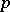 ; see [a4]. The factorization theorem, when applied to permutations (considered as words without repetitions), yields a variant of the so-called Foata transform [a1], Chap. 10.
; see [a4]. The factorization theorem, when applied to permutations (considered as words without repetitions), yields a variant of the so-called Foata transform [a1], Chap. 10.
Given any Lyndon word  , one may compute the factorization of
, one may compute the factorization of 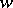 as a product
as a product  , where
, where  is a Lyndon word of maximal length (less than the length of
is a Lyndon word of maximal length (less than the length of  ). The strict suffix (or proper right factor)
). The strict suffix (or proper right factor)  can also be characterized as the smallest strict suffix of
can also be characterized as the smallest strict suffix of  . Then
. Then  is also a Lyndon word and
is also a Lyndon word and  . This factorization of
. This factorization of  is called its right standard factorization. Similarly, one may define its left standard factorization. Let
is called its right standard factorization. Similarly, one may define its left standard factorization. Let  be a mapping from the set of Lyndon words into the free associative algebra on
be a mapping from the set of Lyndon words into the free associative algebra on 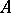 by setting
by setting  , and
, and  , where
, where 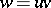 is its right standard factorization. The polynomial thus associated to
is its right standard factorization. The polynomial thus associated to  is a Lie polynomial, and the set
is a Lie polynomial, and the set  forms a linear basis of the free Lie algebra over
forms a linear basis of the free Lie algebra over  (see Lie algebra, free). Note that the iterated right standard factorizations recursively define a bracketing of
(see Lie algebra, free). Note that the iterated right standard factorizations recursively define a bracketing of  (see Binary tree), and thus define a Hall set. The corresponding basis is called the Chen–Fox–Lyndon basis, or simply the Lyndon basis. It is practically identical with the Shirshov basis.
(see Binary tree), and thus define a Hall set. The corresponding basis is called the Chen–Fox–Lyndon basis, or simply the Lyndon basis. It is practically identical with the Shirshov basis.
A good introduction to Lyndon words is [a1], Chap. 5. For applications of Lyndon words related to free Lie algebras, see [a4].
See also Hall word; Hall set; Lazard set.
References
| [a1] | "Combinatorics on words" M. Lothaire (ed.) , Addison-Wesley (1983) |
| [a2] | K.T. Chen, R.H. Fox, R.C. Lyndon, "Free differential calculus, IV. The quotient groups of the lower central series" Ann. of Math. , 68 (1958) pp. 81–95 |
| [a3] | J.P. Duval, "Génération d'une section des classes de conjugaison et arbre de mots de Lyndon de longueur bornée" Theor. Comput. Sci. , 60 (1988) pp. 255–283 |
| [a4] | C. Reutenauer, "Free Lie algebras" , London Math. Soc. Monographs New Ser. , 7 , Oxford Univ. Press (1993) |
| [a5] | J.P. Duval, "Factorizing words over an ordered alphabet" J. Algorithms , 4 (1983) pp. 363–381 |
| [a6] | G. Melançon, C. Reutenauer, "Lyndon words, free algebras and shuffles" Canad. J. Math. , XLI : 4 (1989) pp. 577–591 |
Lyndon word. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lyndon_word&oldid=11373