Lorenz attractor
A compact invariant set $ L $
in the three-dimensional phase space of a smooth flow $ \{ S _ {t} \} $
which has the complicated topological structure mentioned below and is asymptotically stable (that is, it is Lyapunov stable and all trajectories in some neighbourhood of $ L $
tend to $ L $
as $ t \rightarrow \infty $).
The concept of an attractor, that is, an attracting set, often includes only the latter of these two properties; however, both the Lorenz attractor and other practically important attractors have both these properties.
The Lorenz attractor first appeared in numerical experiments of E.N. Lorenz [1], who investigated the behaviour of the trajectories of the system
$$ \tag{* } \dot{x} = - \sigma x + \sigma y ,\ \ \dot{y} = r x - y - x z ,\ \ \dot{z} = - b z + x y $$
for certain specific values of the parameters $ \sigma , r , b $. (This system was initially introduced as the first non-trivial Galerkin approximation for certain hydrodynamical problems; this also motivated the choice of values $ \sigma = 10 $, $ r = 28 $, $ b = 8 / 3 $, but it also arises in other physical problems, see [2], [3].) In
the results of [1] and newer data of numerical experiments were compared in a general way with theoretical ideas in the theory of smooth dynamical systems, and in [5] the results of [1] were interpreted as an indication of the existence in the system (*) of an attractor (called the Lorenz attractor), which in many ways is analogous to hyperbolic sets, cf. Hyperbolic set), but is not such a set (the main difference lies in the fact that a Lorenz attractor contains an equilibrium position of saddle type with one positive eigen value; for the system (*) this equilibrium position is the origin). The existence of a Lorenz attractor and a number of its properties follow from specific properties of the Poincaré return map on some surface $ \Pi $( for the system (*) one uses the plane $ z = 27 $), the exact formulation of which, however, is very unwieldy (see [6], [9], [12], [13]) and in the verification of which for specific systems, including (*), one must recourse to numerical integration. Correspondingly, investigations of two types are devoted to Lorenz attractors.
1) In investigations of theoretical character it is assumed from the very beginning that the flows in question have on some surface $ \Pi $ a suitable Poincaré return map, and from this consequences about the properties of the Lorenz attractor are derived. Its structure is described as follows . Consider a "branched manifold" $ L _ {0} $, on which for $ t \geq 0 $ there is defined a flow $ \phi _ {t} $, as shown in the figure. Suppose that the Poincaré return map on the branch line $ a b $ is (uniformly) expanding, that is, at all points (except $ c $, where it is discontinuous) its derivative is greater than some $ \lambda > 1 $( any such $ \lambda $ is suitable, but the investigation is simplified if $ \lambda > \sqrt 2 $, which is compatible with the computational data concerning the system (*) for the given $ \sigma , r , b $). The pairs $ \{ ( L _ {0} , \phi _ {t} ) \} $ naturally form an inverse spectrum of topological spaces and mappings (cf. Spectrum of spaces); its limit is $ ( L , S _ {t} \mid _ {L} ) $. (Further study of the structure of the Lorenz attractor, , [11], is based on this description, which is therefore naturally included in the definition of the Lorenz attractor, particularly if one does not relate the definition with special properties of the Poincaré map.) Lorenz attractors have topological transitivity and the set of their periodic trajectories is dense in $ L $. Under a small (in the sense of $ C ^ {1} $) perturbation of such a flow having a suitable Poincaré map, the perturbed flow has a Lorenz attractor close to the Lorenz attractor of the original flow, but generally speaking not homeomorphic to it. In this sense a Lorenz attractor is preserved under small perturbations (in the theory of smooth dynamical systems only two classes of compact invariant sets are known (1982) with this property and whose structure is more-or-less well-studied: Lorenz attractors and locally maximal hyperbolic sets (cf. Hyperbolic set), but Lorenz attractors (in contrast to the latter) do not have the property of local structural stability. Ergodic properties of the Lorenz attractor with respect to some "natural" invariant measures are studied in
and [14].
2) In order to discover a Lorenz attractor in a specific system of the type (*) and to determine its properties more exactly, one must use numerical integration together with various theoretical arguments (see , [9]). In this way bifurcations arising in the system (*) as $ r $ or $ \sigma $ vary and leading to the appearance of Lorenz attractors have been investigated [9]. Naturally, numerical integration by itself gives some information about the attractor (since the trajectories approximate it with time, in a figure, showing successive points of intersection of $ \Pi $ with the trajectories being calculated, these points are situated significantly "more densely" along the attractor than far from it, and this immediately strikes the eye).
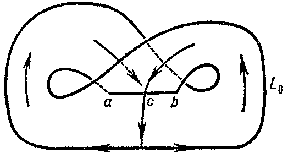
Figure: l060890a
Material on this topic is very extensive; thus, new ranges of values of parameters for which the system (*) has a Lorenz attractor have been found [10]. Here, however, the details of the topological structure, which can differ from the structure of "standard" Lorenz attractors described above, remain unclarified.
A theoretical interpretation of the data of numerical experiments for systems of order greater than three has so far (1982) not been given.
References
| [1] | E.N. Lorenz, "Deterministic non-periodic flow" J. Atmos. Sci. , 20 : 2 (1963) pp. 130–141 |
| [2] | A.S. Monin, "On the nature of turbulence" Soviet Phys. Uspekhi , 21 (1978) pp. 429–442 Uspekhi Fiz. Nauk , 125 : 1 (1978) pp. 97–122 |
| [3] | M.I. Rabinovich, "Stochastic self-oscillations and turbulence" Soviet Phys. Uspekhi , 21 (1978) pp. 443–469 Uspekhi Fiz. Nauk , 125 : 1 (1978) pp. 123–168 |
| [4a] | J.B. McLughlin, P.C. Martin, "Transition to turbulence of a statically stressed fluid system" Phys. Rev. Letters , 33 (1974) pp. 1189–1192 |
| [4b] | J.B. McLughlin, P.C. Martin, "Transition to turbulence of a statically stressed fluid system" Phys. Rev. Ser. A , 12 (1975) pp. 186–203 |
| [5] | D. Ruelle, "The Lorentz attractor and the problem of turbulence" R. Temam (ed.) , Turbulence and Navier–Stokes equations , Lect. notes in math. , 565 , Springer (1976) pp. 146–158 |
| [6] | J.E. Marsden, M. MacCracken, G.F. Oster, "The Hopf bifurcation and its applications" , Springer (1976) ((The Russian translation, Mir (1980), contains an appendix on the Lorenz attractor.)) |
| [7a] | Ya.G. Sinai, "Stochasticity of dynamical systems" , Non-linear waves , Moscow (1979) pp. 192–212 (In Russian) |
| [7b] | Z.A. Bunimovich, Ya.G. Sinai, "Stochasticity of the attractor in the Lorenz model" , Non-linear waves , Moscow (1979) pp. 212–226 (In Russian) |
| [8a] | R.F. Williams, "The structure of Lorenz attractors" R. Temam (ed.) , Turbulence and Navier–Stokes equations , Lect. notes in math. , 565 , Springer (1976) pp. 146–158 |
| [8b] | R.F. Williams, "The structure of Lorenz attractors" Publ. Math. IHES , 50 (1979) pp. 73–100 |
| [9] | V.S. Afraimovich, V.V. Bykov, L.P. Shil'nikov, "On the origin and structure of the Lorenz attractor" Dokl. Akad. Nauk SSSR , 234 : 2 (1977) pp. 336–339 (In Russian) |
| [10] | N. Morioka, T. Shimizu, "Transition between turbulent and periodic states in the Lorenz model" Phys. Letters , 66A : 6 (1978) pp. 447–449 |
| [11] | D. Rand, "The topological classification of Lorenz attractors" Math. Proc. Cambridge Phil. Soc. , 83 : 3 (1978) pp. 451–460 |
| [12] | V.S. Afraimovich, V.V. Bykov, Z.P. Shil'nikov, "On structurally unstable attracting limit sets of Lorenz-attractor type" Trans. Moscow Math. Soc. , 44 (1982) pp. 153–216 Trudy Moscov. Mat. Obshch. , 44 (1982) pp. 150–122 |
| [13] | J. Guckenheimer, R.F. Williams, "Structural stability of Lorenz attractors" Publ. Math. IHES , 50 (1979) pp. 59–72 |
| [14] | Ya. Pesin, "Ergodic properties and dimensionlike characteristics of strange attractors that are close to hyperbolic" A.M. Gleason (ed.) , Proc. Internat. Congress Mathematicians (Berkeley, 1986) , Amer. Math. Soc. (1987) pp. 1195–1209 |
Lorenz attractor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lorenz_attractor&oldid=47716