Locally finite semi-group
A semi-group in which every finitely-generated sub-semi-group is finite. A locally finite semi-group is a periodic semi-group (torsion semi-group). The converse is false: There are even torsion groups that are not locally finite (see Burnside problem). Long before the solution of the Burnside problem for groups, examples had been constructed of semi-groups that are torsion but not locally finite in classes of semi-groups remote from groups; above all, in the class of nil semi-groups (cf. Nil semi-group). These are, for example, a free semi-group with two generators in the variety given by 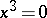 , and a free semi-group with three generators in the variety given by
, and a free semi-group with three generators in the variety given by 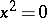 . Moreover, for a number of classes of semi-groups the conditions of periodicity and local finiteness are equivalent. A trivial example is given by commutative semi-groups. A band of locally finite semi-groups (see Band of semi-groups) is itself a locally finite semi-group [1]; moreover, a semi-group that has a decomposition into locally finite groups is a locally finite semi-group; in particular, a semi-group of idempotents (cf. Idempotents, semi-group of) is a locally finite semi-group [7]. If
. Moreover, for a number of classes of semi-groups the conditions of periodicity and local finiteness are equivalent. A trivial example is given by commutative semi-groups. A band of locally finite semi-groups (see Band of semi-groups) is itself a locally finite semi-group [1]; moreover, a semi-group that has a decomposition into locally finite groups is a locally finite semi-group; in particular, a semi-group of idempotents (cf. Idempotents, semi-group of) is a locally finite semi-group [7]. If  is such that any group satisfying the law
is such that any group satisfying the law 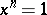 is locally finite, then any semi-group with the law
is locally finite, then any semi-group with the law  is locally finite [6]. A semi-group that has a decomposition into locally finite semi-groups need not be a locally finite semi-group [3], but if
is locally finite [6]. A semi-group that has a decomposition into locally finite semi-groups need not be a locally finite semi-group [3], but if 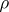 is a congruence on a semi-group
is a congruence on a semi-group 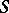 such that the quotient semi-group
such that the quotient semi-group 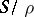 is locally finite and every
is locally finite and every 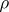 -class that is a sub-semi-group is locally finite, then
-class that is a sub-semi-group is locally finite, then  is a locally finite semi-group (see [4], [5]); in particular, an ideal extension of a locally finite semi-group by a locally finite semi-group is itself a locally finite semi-group. If
is a locally finite semi-group (see [4], [5]); in particular, an ideal extension of a locally finite semi-group by a locally finite semi-group is itself a locally finite semi-group. If  is a periodic semi-group of matrices over a skew-field and all subgroups of
is a periodic semi-group of matrices over a skew-field and all subgroups of 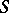 are locally finite, then
are locally finite, then 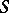 is locally finite [8], which implies that any periodic semi-group of matrices over an arbitrary field is locally finite.
is locally finite [8], which implies that any periodic semi-group of matrices over an arbitrary field is locally finite.
If 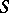 is a periodic inverse semi-group of matrices over a field and, moreover, the periods of all its elements (see Monogenic semi-group) are uniformly bounded and are not divided by the characteristic of the field, then
is a periodic inverse semi-group of matrices over a field and, moreover, the periods of all its elements (see Monogenic semi-group) are uniformly bounded and are not divided by the characteristic of the field, then 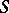 is finite [2].
is finite [2].
References
| [1] | L.N. Shevrin, "On locally finite semigroups" Soviet Math. Dokl. , 6 (1965) pp. 769–772 Dokl. Akad. Nauk SSSR , 162 (1965) pp. 770–773 |
| [2] | L.B. Shneperman, "Periodic inverse linear semigroups" Vesci Akad. Nauk BSSR Ser. Fiz. Mat. Nauk. , 4 (1976) pp. 22–28 (In Russian) |
| [3] | T.C. Brown, "On locally finite semigroups" Ukr. Math. J. , 20 (1968) pp. 631–636 Ukr. Mat. Zh. , 20 : 6 (1968) pp. 732–738 |
| [4] | T.C. Brown, "A semigroup union of disjoint locally finite subsemigroups which is not locally finite" Pacific J. Math. , 22 : 1 (1967) pp. 11–14 |
| [5] | T.C. Brown, "An interesting combinatorial method in the theory of locally finite semigroups" Pacific J. Math. , 36 : 2 (1971) pp. 285–289 |
| [6] | J.A. Green, D. Rees, "On semi-groups in which 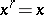 " Proc. Cambridge Philos. Soc. , 48 : 1 (1952) pp. 35–40 " Proc. Cambridge Philos. Soc. , 48 : 1 (1952) pp. 35–40 |
| [7] | D. McLean, "Idempotent semigroups" Amer. Math. Monthly , 61 : 2 (1954) pp. 110–113 |
| [8] | R. McNaughton, Y. Zalcstein, "The Burnside problem for semigroups" J. of Algebra , 34 : 2 (1975) pp. 292–299 |
Locally finite semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Locally_finite_semi-group&oldid=15721