Local and residual properties
Certain abstract properties (that is, properties preserved under isomorphism) of algebraic systems or universal algebras. If 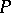 is an abstract property of algebras, one says that an algebra
is an abstract property of algebras, one says that an algebra 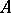 locally has the property
locally has the property 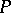 if there is a local system of subalgebras of
if there is a local system of subalgebras of 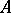 each of which has the property
each of which has the property 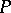 . A local system of subalgebras of
. A local system of subalgebras of 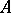 is a system of non-empty subalgebras, directed by inclusion, whose union coincides with
is a system of non-empty subalgebras, directed by inclusion, whose union coincides with 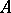 . If every algebra of some class that locally has the property
. If every algebra of some class that locally has the property  actually has the property
actually has the property 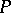 itself, then
itself, then 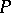 is called a local property of the algebras of this class. For example, the property of being an Abelian group is a local property in the class of all groups, but the property of being a finite group is not local. For more details about the local nature of properties, see Mal'tsev local theorems.
is called a local property of the algebras of this class. For example, the property of being an Abelian group is a local property in the class of all groups, but the property of being a finite group is not local. For more details about the local nature of properties, see Mal'tsev local theorems.
One says that an algebra 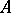 residually has the property
residually has the property 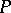 if there is a separating family of congruences
if there is a separating family of congruences 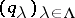 on
on 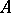 such that every quotient algebra
such that every quotient algebra 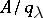 has the property
has the property 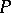 . A family
. A family 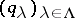 is called a separating family of congruences if the intersection of all the
is called a separating family of congruences if the intersection of all the 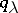 is the diagonal congruence (the equality relation) on the given algebra. An algebra residually has the property
is the diagonal congruence (the equality relation) on the given algebra. An algebra residually has the property 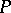 if and only if it can be represented as a subdirect product of algebras of the appropriate type having the property
if and only if it can be represented as a subdirect product of algebras of the appropriate type having the property 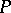 . A property
. A property 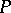 is said to be residual in a class of algebras if every algebra of this class that residually has the property
is said to be residual in a class of algebras if every algebra of this class that residually has the property 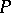 actually has the property
actually has the property  itself. In the class of all groups the property of being Abelian is residual, but finiteness is not residual. Every residual property of algebras that is preserved under transition to homomorphic images is local.
itself. In the class of all groups the property of being Abelian is residual, but finiteness is not residual. Every residual property of algebras that is preserved under transition to homomorphic images is local.
References
| [1] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
Comments
Of course, the precise meaning of the phrase "local property" depends on the local system of algebras that is used to define it.
A most important example of a local system of subalgebras of 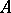 is the system of all finitely-generated subalgebras of
is the system of all finitely-generated subalgebras of 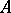 ; see also e.g. Locally free group; Locally solvable group; Locally solvable algebra; Local property; Locally nilpotent group; Locally nilpotent algebra; Locally finite group; Locally finite algebra.
; see also e.g. Locally free group; Locally solvable group; Locally solvable algebra; Local property; Locally nilpotent group; Locally nilpotent algebra; Locally finite group; Locally finite algebra.
The term "local property" is used in topology as well as algebra. If 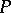 is an abstract property of topological spaces, one says that a space
is an abstract property of topological spaces, one says that a space 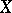 locally has the property
locally has the property 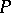 if every point of
if every point of 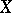 possesses a base of neighbourhoods having the property
possesses a base of neighbourhoods having the property 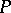 . (For example, the properties "locally compact" and "locally connected" may be defined in this way.) One says that
. (For example, the properties "locally compact" and "locally connected" may be defined in this way.) One says that 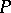 is a local property if the spaces which locally have the property
is a local property if the spaces which locally have the property 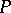 are exactly the
are exactly the 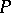 -spaces: for example, the
-spaces: for example, the 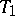 separation axiom is a local property, but the Hausdorff axiom is not.
separation axiom is a local property, but the Hausdorff axiom is not.
Local and residual properties. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Local_and_residual_properties&oldid=12157