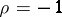Linear system of differential equations with periodic coefficients
A system of  linear ordinary differential equations of the form
linear ordinary differential equations of the form
 | (1) |
where 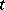 is a real variable,
is a real variable, 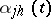 and
and 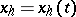 are complex-valued functions, and
are complex-valued functions, and
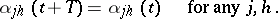 | (2) |
The number 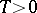 is called the period of the coefficients of the system (1). It is convenient to write (1) as one vector equation
is called the period of the coefficients of the system (1). It is convenient to write (1) as one vector equation
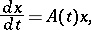 | (3) |
where
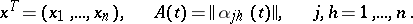 |
It is assumed that the functions 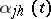 are defined for
are defined for 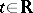 and are measurable and Lebesgue integrable on
and are measurable and Lebesgue integrable on 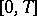 , and that the equalities (2) are satisfied almost-everywhere, that is,
, and that the equalities (2) are satisfied almost-everywhere, that is, 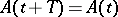 . A solution of (3) is a vector function
. A solution of (3) is a vector function  with absolutely-continuous components such that (3) is satisfied almost-everywhere. Suppose that
with absolutely-continuous components such that (3) is satisfied almost-everywhere. Suppose that 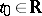 and
and  are an (arbitrarily) given number and vector. A solution
are an (arbitrarily) given number and vector. A solution 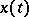 satisfying the condition
satisfying the condition 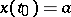 exists and is uniquely determined. A matrix
exists and is uniquely determined. A matrix  of order
of order  with absolutely-continuous entries is called the matrizant (or evolution matrix, or transition matrix, or Cauchy matrix) of (3) if almost-everywhere on
with absolutely-continuous entries is called the matrizant (or evolution matrix, or transition matrix, or Cauchy matrix) of (3) if almost-everywhere on 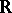 one has
one has
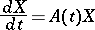 |
and 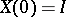 , where
, where 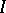 is the unit
is the unit 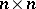 matrix. The transition matrix
matrix. The transition matrix 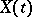 satisfies the relation
satisfies the relation
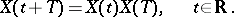 |
The matrix 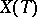 is called the monodromy matrix, and its eigen values
is called the monodromy matrix, and its eigen values 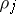 are called the multipliers of (3). The equation
are called the multipliers of (3). The equation
 | (4) |
for the multipliers 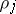 is called the characteristic equation of equation (3) (or of the system (1)). To every eigen vector
is called the characteristic equation of equation (3) (or of the system (1)). To every eigen vector 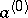 of the monodromy matrix with multiplier
of the monodromy matrix with multiplier 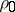 corresponds a solution
corresponds a solution 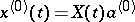 of (3) satisfying the condition
of (3) satisfying the condition
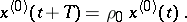 |
The Floquet–Lyapunov theorem holds: The transition matrix of (3) with 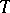 -periodic matrix
-periodic matrix 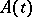 can be represented in the form
can be represented in the form
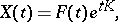 | (5) |
where 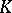 is a constant matrix and
is a constant matrix and 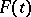 is an absolutely-continuous matrix function, periodic with period
is an absolutely-continuous matrix function, periodic with period 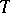 , non-singular for all
, non-singular for all 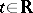 , and such that
, and such that 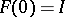 . Conversely, if
. Conversely, if 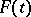 and
and 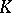 are matrices with the given properties, then the matrix (5) is the transition matrix of an equation (3) with
are matrices with the given properties, then the matrix (5) is the transition matrix of an equation (3) with 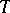 -periodic matrix
-periodic matrix 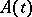 . The matrix
. The matrix 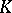 , called the indicator matrix, and the matrix function
, called the indicator matrix, and the matrix function 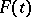 in the representation (5) are not uniquely determined. In the case of real coefficients
in the representation (5) are not uniquely determined. In the case of real coefficients 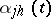 in (5),
in (5), 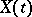 is a real matrix, but
is a real matrix, but 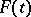 and
and 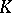 are complex matrices, generally speaking. For this case there is a refinement of the Floquet–Lyapunov theorem: The transition matrix of (3) with
are complex matrices, generally speaking. For this case there is a refinement of the Floquet–Lyapunov theorem: The transition matrix of (3) with 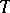 -periodic real matrix
-periodic real matrix 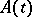 can be represented in the form (5), where
can be represented in the form (5), where 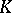 is a constant real matrix and
is a constant real matrix and 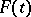 is a real absolutely-continuous matrix function, non-singular for all
is a real absolutely-continuous matrix function, non-singular for all 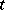 , satisfying the relations
, satisfying the relations
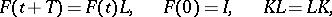 |
where 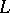 is a real matrix such that
is a real matrix such that
 |
In particular, 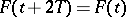 . Conversely, if
. Conversely, if 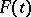 ,
, 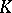 and
and 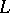 are arbitrary matrices with the given properties, then (5) is the transition matrix of an equation (3) with a
are arbitrary matrices with the given properties, then (5) is the transition matrix of an equation (3) with a 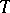 -periodic real matrix
-periodic real matrix 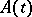 .
.
An immediate consequence of (5) is Floquet's theorem, which asserts that equation (3) has a fundamental system of solutions splitting into subsets, each of which has the form
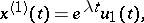 |
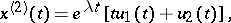 |
 |
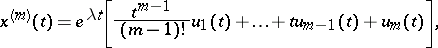 |
where the 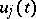 are absolutely-continuous
are absolutely-continuous 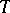 -periodic (generally speaking, complex-valued) vector functions. (The given subset of solutions corresponds to one
-periodic (generally speaking, complex-valued) vector functions. (The given subset of solutions corresponds to one 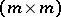 -cell of the Jordan form of
-cell of the Jordan form of 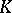 .) If all elementary divisors of
.) If all elementary divisors of 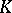 are simple (in particular, if all roots of the characteristic equation (4) are simple), then there is a fundamental system of solutions of the form
are simple (in particular, if all roots of the characteristic equation (4) are simple), then there is a fundamental system of solutions of the form
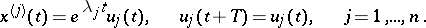 |
Formula (5) implies that (3) is reducible (see Reducible linear system) to the equation
 |
by means of the change of variable  (Lyapunov's theorem).
(Lyapunov's theorem).
Let 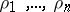 be the multipliers of equation (3) and let
be the multipliers of equation (3) and let 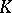 be an arbitrary indicator matrix, that is,
be an arbitrary indicator matrix, that is,
 | (6) |
The eigen values 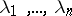 of
of  are called the characteristic exponents (cf. Characteristic exponent) of (3). From (6) one obtains
are called the characteristic exponents (cf. Characteristic exponent) of (3). From (6) one obtains  ,
, 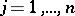 . The characteristic exponent
. The characteristic exponent 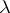 can be defined as the complex number for which (3) has a solution that is representable in the form
can be defined as the complex number for which (3) has a solution that is representable in the form
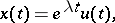 |
where  is a
is a 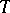 -periodic vector-valued function. The main properties of the solutions in which one is usually interested in applications are determined by the characteristic exponents or multipliers of the given equation (see the Table).'
-periodic vector-valued function. The main properties of the solutions in which one is usually interested in applications are determined by the characteristic exponents or multipliers of the given equation (see the Table).'
<tbody> </tbody>
|
In applications, the coefficients of (1) often depend on parameters; in the parameter space one must distinguish the domains at whose points the solutions of (1) have desired properties (usually these are the first four properties mentioned in the Table, or the fact that 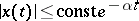 with
with 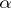 given). These problems thus reduce to the calculation or estimation of the characteristic exponents (multipliers) of (1).
given). These problems thus reduce to the calculation or estimation of the characteristic exponents (multipliers) of (1).
The equation
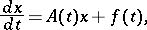 | (7) |
where 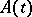 and
and 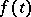 are a measurable
are a measurable 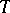 -periodic matrix function and vector function, respectively, that are Lebesgue integrable on
-periodic matrix function and vector function, respectively, that are Lebesgue integrable on 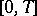 (
( ,
, 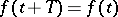 almost-everywhere), is called an "inhomogeneous linear ordinary differential equation with periodic coefficientsinhomogeneous linear ordinary differential equation with periodic coefficients" . If the corresponding homogeneous equation
almost-everywhere), is called an "inhomogeneous linear ordinary differential equation with periodic coefficientsinhomogeneous linear ordinary differential equation with periodic coefficients" . If the corresponding homogeneous equation
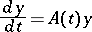 | (8) |
does not have 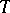 -periodic solutions, then (7) has a unique
-periodic solutions, then (7) has a unique 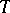 -periodic solution. It can be determined by the formula
-periodic solution. It can be determined by the formula
 |
where 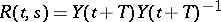 and
and 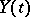 is the transition matrix of the homogeneous equation (8), where
is the transition matrix of the homogeneous equation (8), where 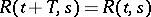 ,
, 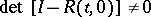 .
.
Suppose that (8) has 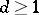 linearly independent
linearly independent 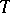 -periodic solutions
-periodic solutions  . Then the adjoint equation
. Then the adjoint equation
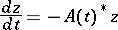 |
also has 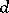 linearly independent
linearly independent 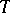 -periodic solutions,
-periodic solutions, 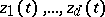 . The inhomogeneous equation (7) has a
. The inhomogeneous equation (7) has a 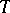 -periodic solution if and only if that the orthogonality relations
-periodic solution if and only if that the orthogonality relations
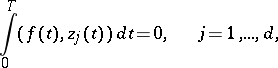 | (9) |
hold. If so, an arbitrary 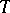 -periodic solution of (7) has the form
-periodic solution of (7) has the form
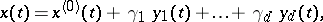 |
where 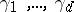 are arbitrary numbers and
are arbitrary numbers and 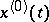 is a
is a 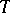 -periodic solution of (7). Under the additional conditions
-periodic solution of (7). Under the additional conditions
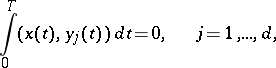 |
the 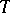 -periodic solution
-periodic solution 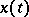 is determined uniquely; moreover, there is a constant
is determined uniquely; moreover, there is a constant  , independent of
, independent of 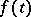 , such that
, such that
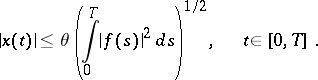 |
Suppose one is given an equation
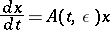 | (10) |
with a matrix coefficient that holomorphically depends on a complex "small" parameter  :
:
 | (11) |
Suppose that for  the series
the series
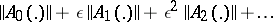 |
converges, where
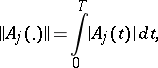 |
which guarantees the (componentwise) convergence of the series (11) for  in the space
in the space  . Then the transition matrix
. Then the transition matrix  of (10) for fixed
of (10) for fixed  is an analytic function of
is an analytic function of  for
for  . Let
. Let 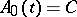 be a constant matrix with eigen values
be a constant matrix with eigen values 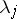 ,
, 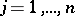 . Let
. Let 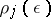 be the multipliers of equation (10),
be the multipliers of equation (10), 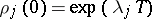 . If
. If 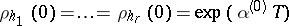 is a multiplier of multiplicity
is a multiplier of multiplicity  , then
, then
 | (12) |
where 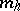 are integers. If simple elementary divisors of the monodromy matrix correspond to this multiplier, or, in other words, if to each
are integers. If simple elementary divisors of the monodromy matrix correspond to this multiplier, or, in other words, if to each 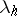 ,
,  , correspond simple elementary divisors of the matrix
, correspond simple elementary divisors of the matrix 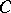 (for example, if all the numbers
(for example, if all the numbers 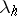 are distinct), then
are distinct), then 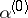 is called an
is called an  -fold characteristic exponent (of equation (10) with
-fold characteristic exponent (of equation (10) with 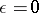 ) of simple type. It turns out that the corresponding
) of simple type. It turns out that the corresponding  characteristic exponents of (10) with small
characteristic exponents of (10) with small 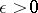 can be very easily computed to a first approximation. Namely, let
can be very easily computed to a first approximation. Namely, let 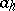 and
and 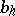 be the corresponding normalized eigen vectors of the matrices
be the corresponding normalized eigen vectors of the matrices 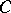 and
and 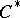 ;
;
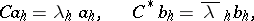 |
 |
let
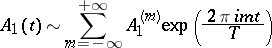 |
be the Fourier series of 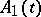 , and let
, and let
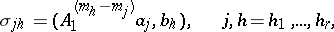 |
where 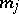 are the numbers from (12). Then for the corresponding
are the numbers from (12). Then for the corresponding  characteristic exponents
characteristic exponents 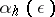 ,
, 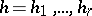 , of (10), which become
, of (10), which become 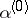 for
for 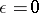 , one has series expansions in fractional powers of
, one has series expansions in fractional powers of  , starting with terms of the first order:
, starting with terms of the first order:
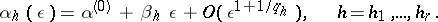 | (13) |
Here the 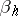 are the roots (written as many times as their multiplicity) of the equation
are the roots (written as many times as their multiplicity) of the equation
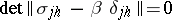 |
and 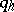 are natural numbers equal to the multiplicities of the corresponding
are natural numbers equal to the multiplicities of the corresponding 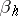 (
(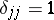 ,
, 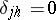 for
for  ). If the root
). If the root  is simple, then
is simple, then 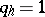 and the corresponding function
and the corresponding function 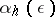 is analytic for
is analytic for 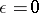 . From (13) it follows that cases are possible in which the "unperturbed" (that is, with
. From (13) it follows that cases are possible in which the "unperturbed" (that is, with  ) system is stable (all the
) system is stable (all the 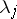 are purely imaginary and simple elementary divisors correspond to them), but the "perturbed" system (small
are purely imaginary and simple elementary divisors correspond to them), but the "perturbed" system (small 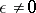 ) is unstable (
) is unstable (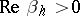 for at least one
for at least one 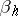 ). This phenomenon of stability loss for an arbitrary small periodic change of parameters (with time) is called parametric resonance. Similar but more complicated formulas hold for characteristic exponents of non-simple type.
). This phenomenon of stability loss for an arbitrary small periodic change of parameters (with time) is called parametric resonance. Similar but more complicated formulas hold for characteristic exponents of non-simple type.
Let 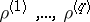 be the distinct multipliers of equation (3) and let
be the distinct multipliers of equation (3) and let 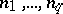 be their multiplicities, where
be their multiplicities, where 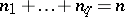 . Suppose that the points
. Suppose that the points 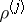 on the complex
on the complex 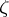 -plane are surrounded by non-intersecting discs
-plane are surrounded by non-intersecting discs 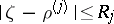 and that a cut, not intersecting these discs, is drawn from the point
and that a cut, not intersecting these discs, is drawn from the point  to the point
to the point 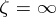 . Suppose that with each multiplier
. Suppose that with each multiplier 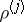 is associated an arbitrary integer
is associated an arbitrary integer 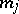 and that
and that 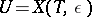 is the transition matrix of (10). The branches of the logarithm
is the transition matrix of (10). The branches of the logarithm 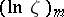 are determined by means of the cut. The matrix
are determined by means of the cut. The matrix 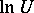 ( "matrix logarithmmatrix logarithm" ) can be defined by the formula
( "matrix logarithmmatrix logarithm" ) can be defined by the formula
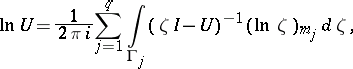 | (14) |
where 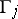 is the circle
is the circle 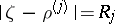 . The set of numbers
. The set of numbers 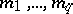 determines a branch of the matrix logarithm. Also,
determines a branch of the matrix logarithm. Also,  for small
for small  . Generally speaking, formula (14) for all possible
. Generally speaking, formula (14) for all possible 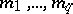 does not cover all the values of the matrix logarithm, that is, all solutions
does not cover all the values of the matrix logarithm, that is, all solutions 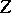 of the equation
of the equation 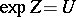 . However, the solution given by (14) has the important property of holomorphy: The entries of the matrix
. However, the solution given by (14) has the important property of holomorphy: The entries of the matrix 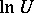 in (14) are holomorphic functions of the entries of
in (14) are holomorphic functions of the entries of 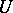 . For equation (10), formula (5) takes the form
. For equation (10), formula (5) takes the form
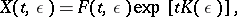 | (15) |
where  ,
, 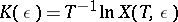 . If
. If 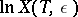 is determined in accordance with (14), then
is determined in accordance with (14), then
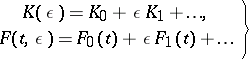 | (16) |
are series that converge for small 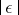 . The main information about the behaviour of the solutions as
. The main information about the behaviour of the solutions as 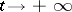 which is usually of interest in applications is contained in the indicator matrix
which is usually of interest in applications is contained in the indicator matrix 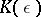 . Below a method for the asymptotic integration of (10) is given, that is, a method for successively determining the coefficients
. Below a method for the asymptotic integration of (10) is given, that is, a method for successively determining the coefficients 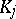 and
and 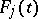 in (16).
in (16).
Suppose that 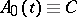 in (11). Although
in (11). Although 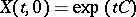 , generally speaking there is no branch of the matrix logarithm such that the matrix
, generally speaking there is no branch of the matrix logarithm such that the matrix 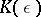 is analytic for
is analytic for 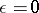 and
and 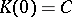 . This branch of the logarithm will exist in the so-called non-resonance case, when among the eigen values
. This branch of the logarithm will exist in the so-called non-resonance case, when among the eigen values 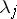 of
of 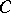 there are no numbers for which
there are no numbers for which
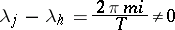 |
(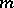 is an integer). In the resonance case (when such eigen values exist) equation (10) reduces by a suitable change of variable
is an integer). In the resonance case (when such eigen values exist) equation (10) reduces by a suitable change of variable 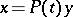 , where
, where 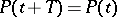 , to an analogous equation for which the non-resonance case holds. The matrix
, to an analogous equation for which the non-resonance case holds. The matrix 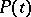 can be determined from the matrix
can be determined from the matrix 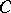 .
.
In (16), in the non-resonance case 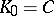 ,
,  , and the matrices
, and the matrices 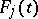 ,
, 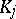 ,
,  are found from the equation
are found from the equation
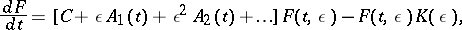 |
after equating coefficients at the same powers of  in this equation. To determine
in this equation. To determine 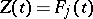 and
and 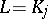 one obtains a matrix equation of the form
one obtains a matrix equation of the form
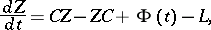 | (17) |
where 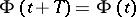 . The matrices
. The matrices 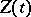 and
and 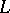 are found, and moreover uniquely (the non-resonance case), from (17) and the periodicity condition
are found, and moreover uniquely (the non-resonance case), from (17) and the periodicity condition 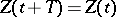 .
.
For special cases of the system (1) see Hamiltonian system, linear and Hill equation.
References
| [1] | I.Z. Shtokalo, "Linear differential equations with variable coefficients: criteria of stability and unstability of their solutions" , Hindushtan Publ. Comp. (1961) (Translated from Russian) |
| [2] | N.P. Erugin, "Linear systems of ordinary differential equations with periodic and quasi-periodic coefficients" , Acad. Press (1966) (Translated from Russian) |
| [3] | V.A. Yakubovich, V.M. Starzhinskii, "Linear differential equations with periodic coefficients" , Wiley (1975) (Translated from Russian) |
Comments
References
| [a1] | R.W. Brockett, "Finite dimensional linear systems" , Wiley (1970) |
| [a2] | J.K. Hale, "Ordinary differential equations" , Wiley (1969) |
Linear system of differential equations with periodic coefficients. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_system_of_differential_equations_with_periodic_coefficients&oldid=16408
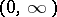 of all solutions)
of all solutions)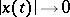 as
as 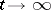 for any solution)
for any solution)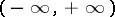
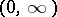 )
)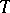 -periodic solution
-periodic solution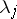 one has
one has 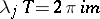 (
(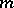 is an integer)
is an integer) for which
for which 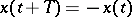 for all
for all 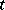
 one has
one has 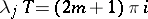 (
(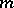 is an integer)
is an integer)