Lindelöf theorem
on asymptotic values
1) Let $ w = f ( z) $ be a bounded regular analytic function in the unit disc $ D = \{ {z } : {| z | < 1 } \} $ and let $ \alpha $ be the asymptotic value of $ f ( z) $ along a Jordan arc $ L $ situated in $ D $ and ending at a point $ e ^ {i \theta _ {0} } $, that is, $ f ( z) \rightarrow \alpha $ as $ z \rightarrow e ^ {i \theta _ {0} } $ along $ L $. Then $ \alpha $ is the angular boundary value (non-tangential boundary value) of $ f ( z) $ at $ e ^ {i \theta _ {0} } $, that is, $ f ( z) $ tends uniformly to $ \alpha $ as $ z \rightarrow e ^ {i \theta _ {0} } $ inside an angle with vertex $ e ^ {i \theta _ {0} } $ formed by two chords of the disc $ D $.
The Lindelöf theorem is also true in domains $ D $ of other types, and the conditions on $ f ( z) $ have been significantly weakened. For example, it is sufficient to require that $ f ( z) $ is a meromorphic function in $ D $ that does not assume three different values. Lindelöf's theorem can also be generalized to functions $ f ( z) $ of several complex variables $ z = ( z _ {1} \dots z _ {n} ) $. For example, if $ f ( z) $ is a bounded holomorphic function in the ball $ D = \{ {z } : {| z | < 1 } \} $ that has asymptotic value $ \alpha $ along a non-tangential path $ L $ at a point $ \zeta \in \partial D $, then $ \alpha $ is the non-tangential boundary value of $ f ( z) $ at $ \zeta $( see [4]).
2) Let $ w = f ( z) $ be a bounded regular analytic function in the disc $ D = \{ {z } : {| z | < 1 } \} $ that has asymptotic values $ \alpha $ and $ \beta $ along two distinct paths $ L _ {1} $ and $ L _ {2} $ that end at the point $ e ^ {i \theta _ {0} } $. Then $ \alpha = \beta $ and $ f ( z) \rightarrow \alpha $ uniformly inside the angle between the paths $ L _ {1} $ and $ L _ {2} $. This theorem is also true for domains $ D $ of other types. For unbounded functions it is false, generally speaking.
These theorems were discovered by E. Lindelöf [1].
References
| [1] | E. Lindelöf, "Sur un principe générale de l'analyse et ses applications à la théorie de la représentation conforme" Acta Soc. Sci. Fennica , 46 : 4 (1915) pp. 1–35 |
| [2] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [3] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 1;6 |
| [4] | E.M. [E.M. Chirka] Čirka, G.M. [G.M. Khenkin] Henkin, "Boundary properties of holomorphic functions of several complex variables" J. Soviet Math. , 5 (1976) pp. 612–687 Itogi Nauk. i Tekhn. Sovrem. Probl. , 4 (1975) pp. 13–142 |
Comments
For the generalization of Lindelöf's theorem to functions of several variables, the condition that the path $ L $ is non-tangential may be weakened, see [a1], Chapt. 8.
References
| [a1] | W. Rudin, "Function theory in the unit ball in 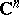 " , Springer (1980) " , Springer (1980) |
Lindelöf theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lindel%C3%B6f_theorem&oldid=47644