Difference between revisions of "Limit-absorption principle"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | l0588301.png | ||
| + | $#A+1 = 67 n = 1 | ||
| + | $#C+1 = 67 : ~/encyclopedia/old_files/data/L058/L.0508830 Limit\AAhabsorption principle | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A manner for uniquely finding solutions to equations analogous to the [[Helmholtz equation|Helmholtz equation]] by introducing an infinitesimal absorption. Mathematically the principle is as follows. Let $ \Omega $ | |
| + | be an unbounded region in $ \mathbf R ^ {n} $, | ||
| + | let $ P $ | ||
| + | be the self-adjoint operator on $ L _ {2} ( \Omega ) $ | ||
| + | given by the differential expression $ P ( x, \partial / \partial x) $, | ||
| + | $ x \in \Omega $, | ||
| + | and homogeneous boundary conditions on $ \Omega $ | ||
| + | and let $ \lambda $ | ||
| + | be a point in the continuous spectrum of $ P $. | ||
| + | Then for $ \epsilon \neq 0 $ | ||
| + | the equation | ||
| − | + | $$ | |
| + | Pu _ \epsilon = \ | ||
| + | ( \lambda + i \epsilon ) | ||
| + | u _ \epsilon + f | ||
| + | $$ | ||
| + | |||
| + | is uniquely solvable in $ L _ {2} ( \Omega ) $, | ||
| + | and in certain cases it is possible to find solutions $ u = u _ \pm $ | ||
| + | of the equation | ||
| + | |||
| + | $$ | ||
| + | Pu = \lambda u + f | ||
| + | $$ | ||
by the limit transition | by the limit transition | ||
| − | + | $$ | |
| + | u _ \pm = \ | ||
| + | \lim\limits _ {\epsilon \rightarrow \pm 0 } \ | ||
| + | u _ \epsilon . | ||
| + | $$ | ||
| + | |||
| + | It is assumed here that $ f $ | ||
| + | has compact support and the convergence $ u _ \epsilon \rightarrow u _ \pm $, | ||
| + | as $ \epsilon \rightarrow \pm 0 $, | ||
| + | is understood in the sense of $ L _ {2} ( \Omega ^ \prime ) $, | ||
| + | where $ \Omega ^ \prime $ | ||
| + | is an arbitrary bounded set in $ \Omega $. | ||
| + | Since $ \lambda $ | ||
| + | is a point of the continuous spectrum of $ P $, | ||
| + | the limit in $ L _ {2} ( \Omega ) $ | ||
| + | does not exist, in general. | ||
| + | |||
| + | The first limit-absorption principle was formulated for the Helmholtz equation in $ \mathbf R ^ {2} $( | ||
| + | cf. [[#References|[1]]]): | ||
| − | + | $$ | |
| + | ( \Delta + k ^ {2} ) u = - f,\ \ | ||
| + | \Omega = \mathbf R ^ {2} , | ||
| + | $$ | ||
| − | + | $$ | |
| + | P = - \Delta ,\ \lambda = - k ^ {2} < 0. | ||
| + | $$ | ||
| − | + | The solutions $ u _ \pm $ | |
| + | found using this principle are diverging or converging waves and satisfy the [[Radiation conditions|radiation conditions]] at infinity. These results were carried over (cf. [[#References|[2]]], [[#References|[3]]]) to elliptic boundary value problems in the exterior of bounded regions in $ \mathbf R ^ {n} $ | ||
| + | for an operator | ||
| − | + | $$ \tag{* } | |
| + | P \left ( x,\ | ||
| + | { | ||
| + | \frac \partial {\partial x } | ||
| + | } | ||
| + | \right ) = - | ||
| + | \sum _ {k, j = 1 } ^ { n } | ||
| + | { | ||
| + | \frac \partial {\partial x _ {k} } | ||
| + | } | ||
| + | \left ( a _ {kj} | ||
| + | \frac \partial {\partial x _ {j} } | ||
| − | + | \right ) + q ( x), | |
| + | $$ | ||
| − | + | where the coefficients $ a _ {kj} ( x) $ | |
| + | tend to constants sufficiently rapidly as $ | x | \rightarrow \infty $. | ||
| + | In order that the limit-absorption principle holds in this case it is necessary that $ \lambda $ | ||
| + | is not an eigen value of $ P $ | ||
| + | or that $ f $ | ||
| + | is orthogonal to the eigen functions. A theorem of T. Kato (cf. [[#References|[3]]]) gives sufficient conditions for the absence of eigen values in the continuous spectrum of the operator $ P = - \Delta + q ( x) $. | ||
| + | Such a theorem has been obtained for the operator (*) (cf. [[#References|[3]]]). The limit-absorption principle has been substantiated for certain regions with non-compact boundary (cf. [[#References|[3]]], [[#References|[4]]]). | ||
| − | + | A limit-absorption principle and corresponding radiation conditions have been found for higher-order equations and for systems of equations (cf. [[#References|[5]]]–[[#References|[7]]]); they consist of the following. Let $ P = ( i \partial / \partial x) $ | |
| + | be an elliptic (or hypo-elliptic) operator satisfying: 1) the polynomial $ P ( \sigma ) $ | ||
| + | has real coefficients; 2) the surface $ P ( \sigma ) = 0 $, | ||
| + | $ \sigma \in \mathbf R ^ {n} $, | ||
| + | decomposes into connected smooth surfaces $ S _ {j} $, | ||
| + | $ 1 \leq j \leq k $, | ||
| + | whose curvatures do not vanish; and 3) $ \mathop{\rm grad} P ( \sigma ) \neq 0 $ | ||
| + | on $ S _ {j} $. | ||
| + | Suppose that an orientation is given on $ S _ {j} $, | ||
| + | i.e. for each surface one has independently chosen a normal direction $ \nu $. | ||
| + | Let $ \omega = x/ | x | $, | ||
| + | let $ \sigma _ {j} = \sigma _ {j} ( \omega ) $ | ||
| + | be a point on $ S _ {j} $ | ||
| + | at which $ \nu $ | ||
| + | and $ \omega $ | ||
| + | have identical direction and let $ \mu _ {j} ( \omega ) = ( \sigma _ {j} ( \omega ), \omega ) $. | ||
| + | Then the function $ u ( x) $ | ||
| + | does satisfy the radiation conditions if it can be represented as | ||
| − | + | $$ | |
| + | u = \sum _ {j = 1 } ^ { k } u _ {j} ( x),\ \ | ||
| + | u _ {j} = O ( r ^ {( 1 - n)/2 } ), | ||
| + | $$ | ||
| − | + | $$ | |
| − | + | \frac{\partial u _ {j} }{\partial r } | |
| + | - i \mu _ {j} ( \omega ) u _ {j} = o ( r ^ {( 1 - n)/2 } ),\ r \rightarrow \infty . | ||
| + | $$ | ||
These conditions determine a unique solution of the equation | These conditions determine a unique solution of the equation | ||
| − | + | $$ | |
| + | P \left ( i | ||
| + | { | ||
| + | \frac \partial {\partial x } | ||
| + | } | ||
| + | \right ) | ||
| + | u = f,\ \ | ||
| + | x \in \mathbf R ^ {n} , | ||
| + | $$ | ||
| − | for any function | + | for any function $ f $ |
| + | with compact support. The limit-absorption principle for this equation is that this solution can be obtained as the limit, for $ \epsilon \rightarrow + 0 $, | ||
| + | of the unique solution $ u _ \epsilon ( x) \in L _ {2} ( \mathbf R ^ {n} ) $ | ||
| + | of the elliptic equation | ||
| − | + | $$ | |
| + | P \left ( i | ||
| + | { | ||
| + | \frac \partial {\partial x } | ||
| + | } | ||
| + | \right ) | ||
| + | u _ \epsilon + i \epsilon Q | ||
| + | \left ( i | ||
| + | { | ||
| + | \frac \partial {\partial x } | ||
| + | } | ||
| + | \right ) | ||
| + | u _ \epsilon = f, | ||
| + | $$ | ||
| − | where | + | where $ Q ( \sigma ) $ |
| + | has real coefficients and $ Q ( \sigma ) \neq 0 $ | ||
| + | on $ S _ {j} $. | ||
| + | Depending on the choice of $ \mathop{\rm sign} _ {\sigma \in S _ {j} } Q ( \sigma ) $, | ||
| + | $ 1 \leq j \leq k $, | ||
| + | one obtains in the limit solutions satisfying the radiation conditions corresponding to some orientation of $ S _ {j} $. | ||
| + | This principle has been substantiated for higher-order equations and systems with variable coefficients in the exterior of bounded regions (cf. [[#References|[5]]]–[[#References|[7]]]), as well as in the case of non-convex $ S _ {j} $. | ||
| + | For such equations there is also a uniqueness theorem of Kato type. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> W. [V.S. Ignatovskii] Ignatowsky, "Reflexion elektromagnetischer Wellen an einem Drahte" ''Ann. der Physik'' , '''18''' : 13 (1905) pp. 495–522</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.Ya. Povzner, "On the decomposition of arbitrary functions into eigenfunctions of the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l058/l058830/l05883068.png" />" ''Mat. Sb.'' , '''32''' : 1 (1953) pp. 109–156 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> D.M. Eidus, "The principle of limiting amplitude" ''Russian Math. Surveys'' , '''24''' : 3 (1969) pp. 97–167 ''Uspekhi Mat. Nauk'' , '''24''' : 3 (1969) pp. 91–156</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.V. Sveshnikov, "The limit absorption principle for a wave guide" ''Dokl. Akad. Nauk SSSR'' , '''80''' : 3 (1951) pp. 345–347 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B.R. Vainberg, "Principles of radiation, limit absorption and limit amplitude in the general theory of partial differential equations" ''Russian Math. Surveys'' , '''21''' : 3 (1966) pp. 115–193 ''Uspekhi Mat. Nauk'' , '''21''' : 3 (1966) pp. 115–194</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B.R. Vainberg, "On elliptic problems in unbounded domains" ''Math. USSR Sb.'' , '''4''' (1968) pp. 419–444 ''Mat. Sb.'' , '''75''' : 3 (1968) pp. 454–480</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> B.R. Vainberg, "Asymptotic methods in equations of mathematical physics" , Gordon & Breach (1988) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> W. [V.S. Ignatovskii] Ignatowsky, "Reflexion elektromagnetischer Wellen an einem Drahte" ''Ann. der Physik'' , '''18''' : 13 (1905) pp. 495–522</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.Ya. Povzner, "On the decomposition of arbitrary functions into eigenfunctions of the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l058/l058830/l05883068.png" />" ''Mat. Sb.'' , '''32''' : 1 (1953) pp. 109–156 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> D.M. Eidus, "The principle of limiting amplitude" ''Russian Math. Surveys'' , '''24''' : 3 (1969) pp. 97–167 ''Uspekhi Mat. Nauk'' , '''24''' : 3 (1969) pp. 91–156</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.V. Sveshnikov, "The limit absorption principle for a wave guide" ''Dokl. Akad. Nauk SSSR'' , '''80''' : 3 (1951) pp. 345–347 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B.R. Vainberg, "Principles of radiation, limit absorption and limit amplitude in the general theory of partial differential equations" ''Russian Math. Surveys'' , '''21''' : 3 (1966) pp. 115–193 ''Uspekhi Mat. Nauk'' , '''21''' : 3 (1966) pp. 115–194</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B.R. Vainberg, "On elliptic problems in unbounded domains" ''Math. USSR Sb.'' , '''4''' (1968) pp. 419–444 ''Mat. Sb.'' , '''75''' : 3 (1968) pp. 454–480</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> B.R. Vainberg, "Asymptotic methods in equations of mathematical physics" , Gordon & Breach (1988) (Translated from Russian)</TD></TR></table> | ||
Revision as of 22:16, 5 June 2020
A manner for uniquely finding solutions to equations analogous to the Helmholtz equation by introducing an infinitesimal absorption. Mathematically the principle is as follows. Let $ \Omega $
be an unbounded region in $ \mathbf R ^ {n} $,
let $ P $
be the self-adjoint operator on $ L _ {2} ( \Omega ) $
given by the differential expression $ P ( x, \partial / \partial x) $,
$ x \in \Omega $,
and homogeneous boundary conditions on $ \Omega $
and let $ \lambda $
be a point in the continuous spectrum of $ P $.
Then for $ \epsilon \neq 0 $
the equation
$$ Pu _ \epsilon = \ ( \lambda + i \epsilon ) u _ \epsilon + f $$
is uniquely solvable in $ L _ {2} ( \Omega ) $, and in certain cases it is possible to find solutions $ u = u _ \pm $ of the equation
$$ Pu = \lambda u + f $$
by the limit transition
$$ u _ \pm = \ \lim\limits _ {\epsilon \rightarrow \pm 0 } \ u _ \epsilon . $$
It is assumed here that $ f $ has compact support and the convergence $ u _ \epsilon \rightarrow u _ \pm $, as $ \epsilon \rightarrow \pm 0 $, is understood in the sense of $ L _ {2} ( \Omega ^ \prime ) $, where $ \Omega ^ \prime $ is an arbitrary bounded set in $ \Omega $. Since $ \lambda $ is a point of the continuous spectrum of $ P $, the limit in $ L _ {2} ( \Omega ) $ does not exist, in general.
The first limit-absorption principle was formulated for the Helmholtz equation in $ \mathbf R ^ {2} $( cf. [1]):
$$ ( \Delta + k ^ {2} ) u = - f,\ \ \Omega = \mathbf R ^ {2} , $$
$$ P = - \Delta ,\ \lambda = - k ^ {2} < 0. $$
The solutions $ u _ \pm $ found using this principle are diverging or converging waves and satisfy the radiation conditions at infinity. These results were carried over (cf. [2], [3]) to elliptic boundary value problems in the exterior of bounded regions in $ \mathbf R ^ {n} $ for an operator
$$ \tag{* } P \left ( x,\ { \frac \partial {\partial x } } \right ) = - \sum _ {k, j = 1 } ^ { n } { \frac \partial {\partial x _ {k} } } \left ( a _ {kj} \frac \partial {\partial x _ {j} } \right ) + q ( x), $$
where the coefficients $ a _ {kj} ( x) $ tend to constants sufficiently rapidly as $ | x | \rightarrow \infty $. In order that the limit-absorption principle holds in this case it is necessary that $ \lambda $ is not an eigen value of $ P $ or that $ f $ is orthogonal to the eigen functions. A theorem of T. Kato (cf. [3]) gives sufficient conditions for the absence of eigen values in the continuous spectrum of the operator $ P = - \Delta + q ( x) $. Such a theorem has been obtained for the operator (*) (cf. [3]). The limit-absorption principle has been substantiated for certain regions with non-compact boundary (cf. [3], [4]).
A limit-absorption principle and corresponding radiation conditions have been found for higher-order equations and for systems of equations (cf. [5]–[7]); they consist of the following. Let $ P = ( i \partial / \partial x) $ be an elliptic (or hypo-elliptic) operator satisfying: 1) the polynomial $ P ( \sigma ) $ has real coefficients; 2) the surface $ P ( \sigma ) = 0 $, $ \sigma \in \mathbf R ^ {n} $, decomposes into connected smooth surfaces $ S _ {j} $, $ 1 \leq j \leq k $, whose curvatures do not vanish; and 3) $ \mathop{\rm grad} P ( \sigma ) \neq 0 $ on $ S _ {j} $. Suppose that an orientation is given on $ S _ {j} $, i.e. for each surface one has independently chosen a normal direction $ \nu $. Let $ \omega = x/ | x | $, let $ \sigma _ {j} = \sigma _ {j} ( \omega ) $ be a point on $ S _ {j} $ at which $ \nu $ and $ \omega $ have identical direction and let $ \mu _ {j} ( \omega ) = ( \sigma _ {j} ( \omega ), \omega ) $. Then the function $ u ( x) $ does satisfy the radiation conditions if it can be represented as
$$ u = \sum _ {j = 1 } ^ { k } u _ {j} ( x),\ \ u _ {j} = O ( r ^ {( 1 - n)/2 } ), $$
$$ \frac{\partial u _ {j} }{\partial r } - i \mu _ {j} ( \omega ) u _ {j} = o ( r ^ {( 1 - n)/2 } ),\ r \rightarrow \infty . $$
These conditions determine a unique solution of the equation
$$ P \left ( i { \frac \partial {\partial x } } \right ) u = f,\ \ x \in \mathbf R ^ {n} , $$
for any function $ f $ with compact support. The limit-absorption principle for this equation is that this solution can be obtained as the limit, for $ \epsilon \rightarrow + 0 $, of the unique solution $ u _ \epsilon ( x) \in L _ {2} ( \mathbf R ^ {n} ) $ of the elliptic equation
$$ P \left ( i { \frac \partial {\partial x } } \right ) u _ \epsilon + i \epsilon Q \left ( i { \frac \partial {\partial x } } \right ) u _ \epsilon = f, $$
where $ Q ( \sigma ) $ has real coefficients and $ Q ( \sigma ) \neq 0 $ on $ S _ {j} $. Depending on the choice of $ \mathop{\rm sign} _ {\sigma \in S _ {j} } Q ( \sigma ) $, $ 1 \leq j \leq k $, one obtains in the limit solutions satisfying the radiation conditions corresponding to some orientation of $ S _ {j} $. This principle has been substantiated for higher-order equations and systems with variable coefficients in the exterior of bounded regions (cf. [5]–[7]), as well as in the case of non-convex $ S _ {j} $. For such equations there is also a uniqueness theorem of Kato type.
References
| [1] | W. [V.S. Ignatovskii] Ignatowsky, "Reflexion elektromagnetischer Wellen an einem Drahte" Ann. der Physik , 18 : 13 (1905) pp. 495–522 |
| [2] | A.Ya. Povzner, "On the decomposition of arbitrary functions into eigenfunctions of the operator 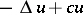 " Mat. Sb. , 32 : 1 (1953) pp. 109–156 (In Russian) " Mat. Sb. , 32 : 1 (1953) pp. 109–156 (In Russian) |
| [3] | D.M. Eidus, "The principle of limiting amplitude" Russian Math. Surveys , 24 : 3 (1969) pp. 97–167 Uspekhi Mat. Nauk , 24 : 3 (1969) pp. 91–156 |
| [4] | A.V. Sveshnikov, "The limit absorption principle for a wave guide" Dokl. Akad. Nauk SSSR , 80 : 3 (1951) pp. 345–347 (In Russian) |
| [5] | B.R. Vainberg, "Principles of radiation, limit absorption and limit amplitude in the general theory of partial differential equations" Russian Math. Surveys , 21 : 3 (1966) pp. 115–193 Uspekhi Mat. Nauk , 21 : 3 (1966) pp. 115–194 |
| [6] | B.R. Vainberg, "On elliptic problems in unbounded domains" Math. USSR Sb. , 4 (1968) pp. 419–444 Mat. Sb. , 75 : 3 (1968) pp. 454–480 |
| [7] | B.R. Vainberg, "Asymptotic methods in equations of mathematical physics" , Gordon & Breach (1988) (Translated from Russian) |
Limit-absorption principle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Limit-absorption_principle&oldid=13580