Difference between revisions of "Lehmer conjecture"
(Tex partly done) |
(Tex partly done) |
||
| Line 9: | Line 9: | ||
and this observation permits one to generalize Mahler's measure to polynomials in several variables (see [[#References|[a11]]], [[#References|[a13]]]). | and this observation permits one to generalize Mahler's measure to polynomials in several variables (see [[#References|[a11]]], [[#References|[a13]]]). | ||
| − | A theorem of L. Kronecker implies that if | + | A theorem of L. Kronecker implies that if $\alpha$ is an algebraic integer with $M(\alpha\le1$, then $\alpha$ is either zero or a root of unity. D.H. Lehmer [[#References|[a7]]] asked whether $M(\alpha$ could attain values arbitrarily close to $1$. This subsequently led to the following formulation of Lehmer's conjecture: There exists a positive constant $\eta$ such that if $\alpha\ne0$ is an algebraic integer, not a root of unity, then |
| + | $$ | ||
| + | M(\alpha) \ge 1 + \eta \ . | ||
| + | $$ | ||
| − | + | Lehmer's conjecture is equivalent to the existence of ergodic automorphisms of the infinite-dimensional torus having finite [[entropy]] [[#References|[a8]]] and its truth would imply the following conjecture stated by A. Schinzel and H. Zassenhaus [[#References|[a16]]]: There exists a positive constant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130020/l13002022.png" /> with the property that if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130020/l13002023.png" /> is a non-zero algebraic integer of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130020/l13002024.png" />, not a root of unity, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130020/l13002025.png" />, the maximal absolute value of a conjugate of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130020/l13002026.png" /> is at least | |
| − | |||
| − | Lehmer's conjecture is equivalent to the existence of ergodic automorphisms of the infinite-dimensional torus having finite [[ | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130020/l13002027.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130020/l13002027.png" /></td> </tr></table> | ||
| Line 40: | Line 41: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.E. Blanksby, H.L. Montgomery, "Algebraic integers near the unit circle" ''Acta Arith.'' , '''18''' (1971) pp. 355–369</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> K. Breusch, "On the distribution of the roots of a polynomial with integral coefficients" ''Proc. Amer. Math. Soc.'' , '''3''' (1951) pp. 939–941</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D.G. Cantor, E.G. Straus, "On a conjecture of D.H. Lehmer" ''Acta Arith.'' , '''42''' (1982) pp. 97–100; 325</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> E. Dobrowolski, "On a question of Lehmer and the number of irreducible factors of a polynomial" ''Acta Arith.'' , '''34''' (1979) pp. 391–401</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> A. Dubickas, "On algebraic numbers of small measure" ''Liet. Mat. Rink.'' , '''35''' (1995) pp. 421–431</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> A. Dubickas, "Algebraic conjugates outside the unit circle" , ''New Trends in Probability and Statistics'' , '''4''' (1997) pp. 11–21</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> D.H. Lehmer, "Factorization of certain cyclotomic functions" ''Ann. Math.'' , '''34''' : 2 (1933) pp. 461–479</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> D.A. Lind, K. Schmidt, T. Ward, "Mahler measure and entropy for commuting automorphisms of compact groups" ''Invent. Math.'' , '''101''' (1990) pp. 503–629</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> R. Louboutin, "Sur la mesure de Mahler d'un nombre algébrique" ''C.R. Acad. Sci. Paris'' , '''296''' (1983) pp. 707–708</TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> K. Mahler, "An application of Jensen's formula to polynomials" ''Mathematika'' , '''7''' (1960) pp. 98–100</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> K. Mahler, "On some inequalities for polynomials in several variables" ''J. London Math. Soc.'' , '''37''' (1962) pp. 341–344</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> U. Rausch, "On a theorem of Dobrowolski about the product of conjugate numbers" ''Colloq. Math.'' , '''50''' (1985) pp. 137–142</TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> A. Schinzel, "The Mahler measure of polynomials" , ''Number Theory and its Applications (Ankara, 1996)'' , M. Dekker (1999) pp. 171–183</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> C.J. Smyth, "On the product of the conjugates outside the unit circle of an algebraic integer" ''Bull. London Math. Soc.'' , '''3''' (1971) pp. 169–175</TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> C.L. Stewart, "Algebraic integers whose conjugates lie near the unit circle" ''Bull. Soc. Math. France'' , '''196''' (1978) pp. 169–176</TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> A. Schinzel, H. Zassenhaus, "A refinement of two theorems of Kronecker" ''Michigan J. Math.'' , '''12''' (1965) pp. 81–85</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> P.E. Blanksby, H.L. Montgomery, "Algebraic integers near the unit circle" ''Acta Arith.'' , '''18''' (1971) pp. 355–369</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> K. Breusch, "On the distribution of the roots of a polynomial with integral coefficients" ''Proc. Amer. Math. Soc.'' , '''3''' (1951) pp. 939–941</TD></TR> | ||
| + | <TR><TD valign="top">[a3]</TD> <TD valign="top"> D.G. Cantor, E.G. Straus, "On a conjecture of D.H. Lehmer" ''Acta Arith.'' , '''42''' (1982) pp. 97–100; 325</TD></TR> | ||
| + | <TR><TD valign="top">[a4]</TD> <TD valign="top"> E. Dobrowolski, "On a question of Lehmer and the number of irreducible factors of a polynomial" ''Acta Arith.'' , '''34''' (1979) pp. 391–401</TD></TR> | ||
| + | <TR><TD valign="top">[a5]</TD> <TD valign="top"> A. Dubickas, "On algebraic numbers of small measure" ''Liet. Mat. Rink.'' , '''35''' (1995) pp. 421–431</TD></TR>< | ||
| + | TR><TD valign="top">[a6]</TD> <TD valign="top"> A. Dubickas, "Algebraic conjugates outside the unit circle" , ''New Trends in Probability and Statistics'' , '''4''' (1997) pp. 11–21</TD></TR> | ||
| + | <TR><TD valign="top">[a7]</TD> <TD valign="top"> D.H. Lehmer, "Factorization of certain cyclotomic functions" ''Ann. Math.'' , '''34''' : 2 (1933) pp. 461–479</TD></TR> | ||
| + | <TR><TD valign="top">[a8]</TD> <TD valign="top"> D.A. Lind, K. Schmidt, T. Ward, "Mahler measure and entropy for commuting automorphisms of compact groups" ''Invent. Math.'' , '''101''' (1990) pp. 503–629</TD></TR> | ||
| + | <TR><TD valign="top">[a9]</TD> <TD valign="top"> R. Louboutin, "Sur la mesure de Mahler d'un nombre algébrique" ''C.R. Acad. Sci. Paris'' , '''296''' (1983) pp. 707–708</TD></TR> | ||
| + | <TR><TD valign="top">[a10]</TD> <TD valign="top"> K. Mahler, "An application of Jensen's formula to polynomials" ''Mathematika'' , '''7''' (1960) pp. 98–100</TD></TR> | ||
| + | <TR><TD valign="top">[a11]</TD> <TD valign="top"> K. Mahler, "On some inequalities for polynomials in several variables" ''J. London Math. Soc.'' , '''37''' (1962) pp. 341–344</TD></TR> | ||
| + | <TR><TD valign="top">[a12]</TD> <TD valign="top"> U. Rausch, "On a theorem of Dobrowolski about the product of conjugate numbers" ''Colloq. Math.'' , '''50''' (1985) pp. 137–142</TD></TR> | ||
| + | <TR><TD valign="top">[a13]</TD> <TD valign="top"> A. Schinzel, "The Mahler measure of polynomials" , ''Number Theory and its Applications (Ankara, 1996)'' , M. Dekker (1999) pp. 171–183</TD></TR> | ||
| + | <TR><TD valign="top">[a14]</TD> <TD valign="top"> C.J. Smyth, "On the product of the conjugates outside the unit circle of an algebraic integer" ''Bull. London Math. Soc.'' , '''3''' (1971) pp. 169–175</TD></TR> | ||
| + | <TR><TD valign="top">[a15]</TD> <TD valign="top"> C.L. Stewart, "Algebraic integers whose conjugates lie near the unit circle" ''Bull. Soc. Math. France'' , '''196''' (1978) pp. 169–176</TD></TR> | ||
| + | <TR><TD valign="top">[a16]</TD> <TD valign="top"> A. Schinzel, H. Zassenhaus, "A refinement of two theorems of Kronecker" ''Michigan J. Math.'' , '''12''' (1965) pp. 81–85</TD></TR> | ||
| + | </table> | ||
{{TEX|part}} | {{TEX|part}} | ||
Revision as of 16:36, 25 March 2018
A conjecture about the minimal Mahler measure of a non-zero algebraic integer which is not a root of unity. The Mahler measure $M(\alpha)$ of an algebraic number $\alpha$ is defined by $$ M(\alpha) = a_0 \prod_{i=1}^N \max(1,|\alpha_i|) \ , $$ where $a_0$ denotes the leading coefficient and $N$ the degree of the minimal polynomial $f$ (with integral coefficients) of $\alpha$ (cf. also Algebraic number) and $\alpha=\alpha_1,\alpha_2,\ldots,\alpha_N$ are its conjugates. Since $M(\alpha)$ depends only on $f$, it is also denoted by $M(f)$ and called the Mahler measure of $f$. Jensen's formula (cf. also Jensen formula) implies the equality $$ M(f) = \exp\left({ \int_0^1 \log\left\vert{ f\left({ e^{2\pi i t} }\right) }\right\vert d t }\right) $$ and this observation permits one to generalize Mahler's measure to polynomials in several variables (see [a11], [a13]).
A theorem of L. Kronecker implies that if $\alpha$ is an algebraic integer with $M(\alpha\le1$, then $\alpha$ is either zero or a root of unity. D.H. Lehmer [a7] asked whether $M(\alpha$ could attain values arbitrarily close to $1$. This subsequently led to the following formulation of Lehmer's conjecture: There exists a positive constant $\eta$ such that if $\alpha\ne0$ is an algebraic integer, not a root of unity, then $$ M(\alpha) \ge 1 + \eta \ . $$
Lehmer's conjecture is equivalent to the existence of ergodic automorphisms of the infinite-dimensional torus having finite entropy [a8] and its truth would imply the following conjecture stated by A. Schinzel and H. Zassenhaus [a16]: There exists a positive constant 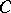 with the property that if
with the property that if 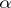 is a non-zero algebraic integer of degree
is a non-zero algebraic integer of degree  , not a root of unity, then
, not a root of unity, then 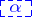 , the maximal absolute value of a conjugate of
, the maximal absolute value of a conjugate of 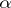 is at least
is at least
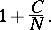 |
It is known ([a2], [a14]) that Lehmer's conjecture holds for non-reciprocal integers 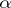 , i.e. algebraic integers whose minimal polynomials do not have
, i.e. algebraic integers whose minimal polynomials do not have 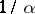 as a root. In this case the minimal value for
as a root. In this case the minimal value for 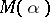 equals
equals 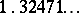 and is attained by roots of the polynomial
and is attained by roots of the polynomial 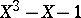 .
.
In 1971, P.E. Blanksby and H.L. Montgomery [a1] established, for all algebraic integers 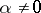 of degree
of degree 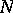 that are not roots of unity, the inequality
that are not roots of unity, the inequality
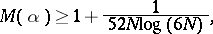 |
and subsequently E. Dobrowolski [a4] obtained
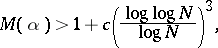 |
with 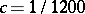 , whereas for
, whereas for 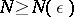 he got
he got  . Subsequently, several authors increased the value of
. Subsequently, several authors increased the value of  to
to 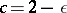 ([a3], [a12]) and
([a3], [a12]) and  ([a9]). Since for non-reciprocal integers
([a9]). Since for non-reciprocal integers 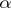 one has
one has  , the last result leads to the inequality
, the last result leads to the inequality
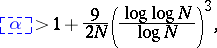 |
but this has been superseded by A. Dubickas [a5], who proved for sufficiently large  the inequality
the inequality
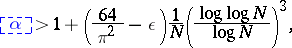 |
which is the strongest known result toward the Schinzel–Zassenhaus conjecture as of 2000.
The smallest known value of 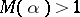 is
is  , realized by the root of
, realized by the root of 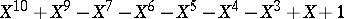 and found in [a7].
and found in [a7].
References
< TR>| [a1] | P.E. Blanksby, H.L. Montgomery, "Algebraic integers near the unit circle" Acta Arith. , 18 (1971) pp. 355–369 |
| [a2] | K. Breusch, "On the distribution of the roots of a polynomial with integral coefficients" Proc. Amer. Math. Soc. , 3 (1951) pp. 939–941 |
| [a3] | D.G. Cantor, E.G. Straus, "On a conjecture of D.H. Lehmer" Acta Arith. , 42 (1982) pp. 97–100; 325 |
| [a4] | E. Dobrowolski, "On a question of Lehmer and the number of irreducible factors of a polynomial" Acta Arith. , 34 (1979) pp. 391–401 |
| [a5] | A. Dubickas, "On algebraic numbers of small measure" Liet. Mat. Rink. , 35 (1995) pp. 421–431 |
| [a6] | A. Dubickas, "Algebraic conjugates outside the unit circle" , New Trends in Probability and Statistics , 4 (1997) pp. 11–21 |
| [a7] | D.H. Lehmer, "Factorization of certain cyclotomic functions" Ann. Math. , 34 : 2 (1933) pp. 461–479 |
| [a8] | D.A. Lind, K. Schmidt, T. Ward, "Mahler measure and entropy for commuting automorphisms of compact groups" Invent. Math. , 101 (1990) pp. 503–629 |
| [a9] | R. Louboutin, "Sur la mesure de Mahler d'un nombre algébrique" C.R. Acad. Sci. Paris , 296 (1983) pp. 707–708 |
| [a10] | K. Mahler, "An application of Jensen's formula to polynomials" Mathematika , 7 (1960) pp. 98–100 |
| [a11] | K. Mahler, "On some inequalities for polynomials in several variables" J. London Math. Soc. , 37 (1962) pp. 341–344 |
| [a12] | U. Rausch, "On a theorem of Dobrowolski about the product of conjugate numbers" Colloq. Math. , 50 (1985) pp. 137–142 |
| [a13] | A. Schinzel, "The Mahler measure of polynomials" , Number Theory and its Applications (Ankara, 1996) , M. Dekker (1999) pp. 171–183 |
| [a14] | C.J. Smyth, "On the product of the conjugates outside the unit circle of an algebraic integer" Bull. London Math. Soc. , 3 (1971) pp. 169–175 |
| [a15] | C.L. Stewart, "Algebraic integers whose conjugates lie near the unit circle" Bull. Soc. Math. France , 196 (1978) pp. 169–176 |
| [a16] | A. Schinzel, H. Zassenhaus, "A refinement of two theorems of Kronecker" Michigan J. Math. , 12 (1965) pp. 81–85 |
Lehmer conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lehmer_conjecture&oldid=43023