Lefschetz theorem
Lefschetz' fixed-point theorem, or the Lefschetz–Hopf theorem, is a theorem that makes it possible to express the number of fixed points of a continuous mapping in terms of its Lefschetz number. Thus, if a continuous mapping 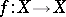 of a finite CW-complex (cf. also Cellular space)
of a finite CW-complex (cf. also Cellular space) 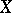 has no fixed points, then its Lefschetz number
has no fixed points, then its Lefschetz number 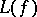 is equal to zero. A special case of this assertion is Brouwer's fixed-point theorem (cf. Brouwer theorem).
is equal to zero. A special case of this assertion is Brouwer's fixed-point theorem (cf. Brouwer theorem).
Comments
References
| [a1] | M.J. Greenberg, J.R. Harper, "Algebraic topology, a first course" , Benjamin/Cummings (1981) MR643101 Zbl 0498.55001 |
Lefschetz' hyperplane-section theorem, or the weak Lefschetz theorem: Let 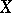 be an algebraic subvariety (cf. Algebraic variety) of complex dimension
be an algebraic subvariety (cf. Algebraic variety) of complex dimension  in the complex projective space
in the complex projective space 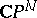 , let
, let 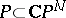 be a hyperplane passing through all singular points of
be a hyperplane passing through all singular points of 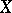 (if any) and let
(if any) and let 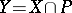 be a hyperplane section of
be a hyperplane section of 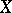 ; then the relative homology groups (cf. Homology group)
; then the relative homology groups (cf. Homology group) 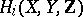 vanish for
vanish for 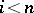 . This implies that the natural homomorphism
. This implies that the natural homomorphism
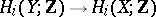 |
is an isomorphism for 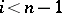 and is surjective for
and is surjective for 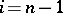 (see ).
(see ).
Using universal coefficient formulas (cf. Künneth formula) one obtains corresponding assertions for arbitrary cohomology groups. In every case, for cohomology with coefficients in the field of rational numbers the dual assertions hold: The homomorphism of cohomology spaces
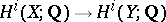 |
induced by the imbedding 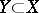 is an isomorphism for
is an isomorphism for 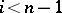 and is injective for
and is injective for 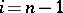 (see ).
(see ).
An analogous assertion is true for homotopy groups: 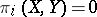 for
for 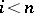 . In particular, the canonical homomorphism
. In particular, the canonical homomorphism 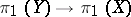 is an isomorphism for
is an isomorphism for 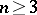 and is surjective for
and is surjective for 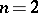 (the Lefschetz theorem on the fundamental group). There is a generalization of this theorem to the case of an arbitrary algebraically closed field (see ), and also to the case when
(the Lefschetz theorem on the fundamental group). There is a generalization of this theorem to the case of an arbitrary algebraically closed field (see ), and also to the case when 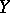 is a normal complete intersection of
is a normal complete intersection of 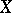 (see ).
(see ).
The hard Lefschetz theorem is a theorem about the existence of a Lefschetz decomposition of the cohomology of a complex Kähler manifold into primitive components.
Let 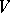 be a compact Kähler manifold of dimension
be a compact Kähler manifold of dimension  with Kähler form
with Kähler form 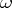 , let
, let
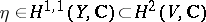 |
be the cohomology class of type 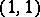 corresponding to
corresponding to 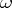 under the de Rham isomorphism (cf. de Rham cohomology; if
under the de Rham isomorphism (cf. de Rham cohomology; if 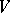 is a projective algebraic variety over
is a projective algebraic variety over 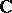 with the natural Hodge metric, then
with the natural Hodge metric, then 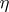 is the cohomology class dual to the homology class of a hyperplane section) and let
is the cohomology class dual to the homology class of a hyperplane section) and let
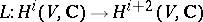 |
be the linear operator defined by multiplication by 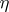 , that is,
, that is,
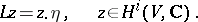 |
One has the isomorphism (see )
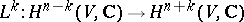 |
for any 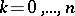 . The kernel of the operator
. The kernel of the operator
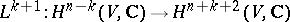 |
is denoted by 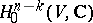 and is called the primitive part of the
and is called the primitive part of the 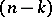 -cohomology of the variety
-cohomology of the variety 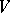 . The elements of
. The elements of 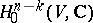 are called primitive cohomology classes, and the cycles corresponding to them are called primitive cycles. The hard Lefschetz theorem establishes the following decomposition of the cohomology into the direct sum of primitives (called the Lefschetz decomposition):
are called primitive cohomology classes, and the cycles corresponding to them are called primitive cycles. The hard Lefschetz theorem establishes the following decomposition of the cohomology into the direct sum of primitives (called the Lefschetz decomposition):
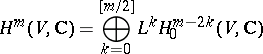 |
for all 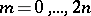 . The mappings
. The mappings
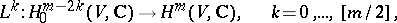 |
are imbeddings. The Lefschetz decomposition commutes with the Hodge decomposition (cf. Hodge conjecture)
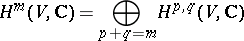 |
(see ). In particular, the primitive part 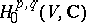 of
of 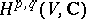 is defined and
is defined and
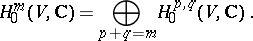 |
The hard Lefschetz theorem and the Lefschetz decomposition have analogues in abstract algebraic geometry for 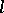 -adic and crystalline cohomology (see , ).
-adic and crystalline cohomology (see , ).
The Lefschetz theorem on cohomology of type 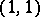 is a theorem about the correspondence between the two-dimensional algebraic cohomology classes of a complex algebraic variety and the cohomology classes of type
is a theorem about the correspondence between the two-dimensional algebraic cohomology classes of a complex algebraic variety and the cohomology classes of type 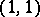 .
.
Let 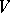 be a non-singular projective algebraic variety over the field
be a non-singular projective algebraic variety over the field  . An element
. An element 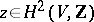 is said to be algebraic if the cohomology class dual to it (in the sense of Poincaré) is determined by a certain divisor. The Lefschetz theorem on cohomology of type
is said to be algebraic if the cohomology class dual to it (in the sense of Poincaré) is determined by a certain divisor. The Lefschetz theorem on cohomology of type 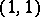 asserts that a class
asserts that a class 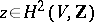 is algebraic if and only if
is algebraic if and only if
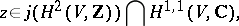 |
where 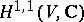 is the Hodge component of type
is the Hodge component of type 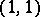 of the two-dimensional complex cohomology space
of the two-dimensional complex cohomology space 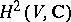 , and the mapping
, and the mapping 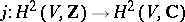 is induced by the natural imbedding
is induced by the natural imbedding 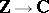 (see [1], and also [6], [12]). For algebraic cohomology classes in dimensions greater than 2, see Hodge conjecture.
(see [1], and also [6], [12]). For algebraic cohomology classes in dimensions greater than 2, see Hodge conjecture.
For an arbitrary complex-analytic manifold 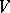 there is an analogous characterization of elements of the group
there is an analogous characterization of elements of the group 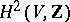 that are Chern classes of complex line bundles over
that are Chern classes of complex line bundles over 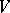 (see [11]).
(see [11]).
References
| [1] | S. Lefschetz, "L'analysis situs et la géométrie algébrique" , Gauthier-Villars (1950) MR0033557 |
| [2] | S. Lefschetz, "On certain numerical invariants of algebraic varieties with applications to Abelian varieties" Trans. Amer. Math. Soc. , 22 (1921) pp. 327–482 MR1501180 MR1501178 |
| [3] | S. Lefschetz, "On the fixed point formula" Ann. of Math. (2) , 38 (1937) pp. 819–822 MR1503373 Zbl 0018.17703 Zbl 63.0563.02 |
| [4] | P. Berthelot, "Cohomologie cristalline des schémas de caractéristique 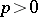 " , Springer (1974) MR0384804 Zbl 0298.14012 " , Springer (1974) MR0384804 Zbl 0298.14012 |
| [5] | P. Deligne (ed.) N.M. Katz (ed.) , Groupes de monodromie en géométrie algébrique. SGA 7.II , Lect. notes in math. , 340 , Springer (1973) MR0354657 |
| [6] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) MR0507725 Zbl 0408.14001 |
| [7] | A. Grothendieck, "Cohomologie locale des faisceaux cohérents et théorèmes de Lefschetz locaux et globaux" , SGA 2 , North-Holland & Masson (1968) MR0476737 Zbl 1079.14001 Zbl 0159.50402 |
| [8] | R. Hartshorne, "Ample subvarieties of algebraic varieties" , Springer (1970) MR0282977 Zbl 0208.48901 |
| [9] | D. Mumford, "Abelian varieties" , Oxford Univ. Press (1974) MR2514037 MR1083353 MR0352106 MR0441983 MR0282985 MR0248146 MR0219542 MR0219541 MR0206003 MR0204427 Zbl 0326.14012 |
| [10] | J.W. Milnor, "Morse theory" , Princeton Univ. Press (1963) MR0163331 Zbl 0108.10401 |
| [11] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) MR0608414 Zbl 0435.32004 |
| [12] | S.S. Chern, "Complex manifolds without potential theory" , Springer (1979) MR0533884 Zbl 0444.32004 |
| [13] | A. Weil, "Introduction à l'Aeetude des variétés kahlériennes" , Hermann (1958) |
| [14] | P. Deligne, "La conjecture de Weil" Publ. Math. IHES , 43 (1974) pp. 273–307 MR0340258 Zbl 0456.14014 Zbl 0314.14007 Zbl 0287.14001 Zbl 0219.14022 |
V.A. Iskovskikh
Comments
For a modern treatment of the classical Lefschetz hyperplane-section theorems see [a1].
Weak and hard (strong) Lefschetz theorems also hold in étale cohomology [a4] and in intersection homology [a5], [a6]. For the proof of the hard Lefschetz theorem in 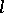 -adic cohomology, see [a2].
-adic cohomology, see [a2].
References
| [a1] | K. Lamotke, "The topology of complex projective varieties after S. Lefschetz" Topology , 20 (1981) pp. 15–51 MR0592569 Zbl 0445.14010 |
| [a2] | P. Deligne, "La conjecture de Weil II" Publ. Math. IHES , 52 (1980) pp. 137–252 MR0601520 Zbl 0456.14014 |
| [a3] | M.J. Greenberg, J.R. Harper, "Algebraic topology, a first course" , Benjamin/Cummings (1981) MR643101 Zbl 0498.55001 |
| [a4] | J.S. Milne, "Etale cohomology" , Princeton Univ. Press (1980) MR0559531 Zbl 0433.14012 |
| [a5] | M. Goresky, "Stratified Morse theory" , Springer (1988) MR0932724 Zbl 0639.14012 |
| [a6] | A. Beilinson, J. Bernstein, P. Deligne, "Faisceaux pervers" Astérisque , 100 (1982) MR0751966 Zbl 0536.14011 |
Lefschetz theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lefschetz_theorem&oldid=23883