Lambda-ring
A pre-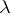 -ring is a commutative ring
-ring is a commutative ring 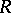 with identity element and a set of mappings
with identity element and a set of mappings 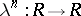 ,
, 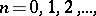 such that
such that
i) 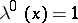 for all
for all 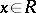 ;
;
ii) 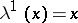 for all
for all 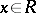 ;
;
iii) 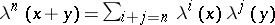 .
.
Examples are, for instance, the topological 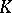 -groups
-groups  and
and  ,
, 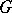 a compact Lie group (cf.
a compact Lie group (cf. 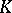 -theory), and the complex representation ring
-theory), and the complex representation ring 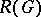 of a finite group
of a finite group 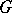 (cf. Representation of a compact group). In all these cases the
(cf. Representation of a compact group). In all these cases the 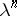 are induced by taking exterior powers. For instance, for
are induced by taking exterior powers. For instance, for 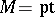 ,
, 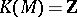 and the
and the 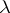 -structure is given by
-structure is given by 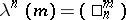 (binomial coefficients; the formula
(binomial coefficients; the formula 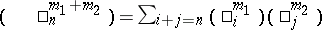 follows by the binomial expansion theorem from
follows by the binomial expansion theorem from 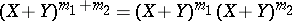 .
.
Let 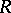 be any commutative ring with unit element 1. Consider the set
be any commutative ring with unit element 1. Consider the set 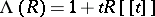 of power series in
of power series in 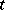 over
over 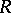 with constant term 1. Multiplication of power series turns
with constant term 1. Multiplication of power series turns 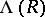 into an Abelian group. A pre-
into an Abelian group. A pre-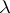 -ring structure on
-ring structure on 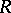 defines a homomorphism of Abelian groups
defines a homomorphism of Abelian groups 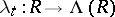 ,
, 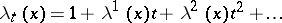 , and vice versa.
, and vice versa.
Let 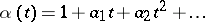 ,
, 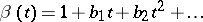 be two elements of
be two elements of 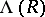 . Formally, write
. Formally, write
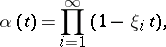 |
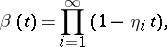 |
and consider the expressions
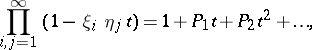 |
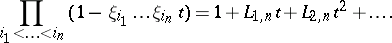 |
The 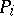 and
and 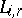 are symmetric polynomial expressions in the
are symmetric polynomial expressions in the 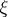 's and
's and 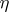 's and hence can be written as universal polynomial expressions in the
's and hence can be written as universal polynomial expressions in the  's and
's and 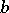 's. Now define a multiplication on
's. Now define a multiplication on 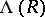 by
by
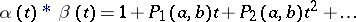 |
(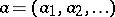 ,
, 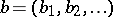 ), and define operations (mappings)
), and define operations (mappings) 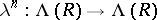 by
by
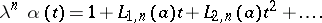 |
The ring 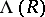 with these operations is a pre-
with these operations is a pre-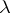 -ring. Given two pre-
-ring. Given two pre-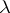 -rings
-rings 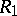 ,
, 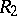 , a
, a 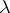 -ring homomorphism
-ring homomorphism 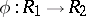 is a homomorphism of rings such that
is a homomorphism of rings such that 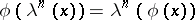 for all
for all 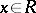 ,
, 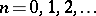 .
.
A pre-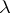 -ring
-ring 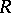 is a
is a 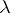 -ring if
-ring if 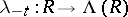 ,
, 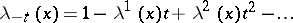 , is a homomorphism of pre-
, is a homomorphism of pre-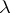 -rings. The ring
-rings. The ring 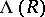 is always a
is always a 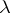 -ring and so are the standard examples
-ring and so are the standard examples 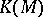 ,
, 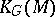 ,
, 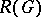 of pre-
of pre-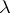 -rings mentioned above.
-rings mentioned above.
On the other hand, consider a finite group 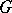 . A finite
. A finite 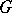 -set is a finite set together with an action of
-set is a finite set together with an action of 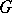 on it. Using disjoint union and Cartesian products with diagonal action, the isomorphism classes of finite
on it. Using disjoint union and Cartesian products with diagonal action, the isomorphism classes of finite 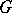 -sets form a semi-ring,
-sets form a semi-ring, 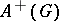 . The associated Grothendieck ring
. The associated Grothendieck ring 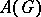 (cf. Grothendieck group) is called the Burnside ring. On
(cf. Grothendieck group) is called the Burnside ring. On 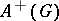 , define operations
, define operations 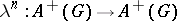 by
by 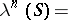 (set of
(set of  -element subsets of
-element subsets of 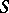 ) (with the natural induced
) (with the natural induced 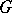 -action). This generalizes the
-action). This generalizes the 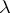 -operations
-operations 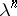 on
on 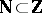 ,
, 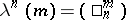 . Using iii), the
. Using iii), the 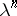 extend to
extend to 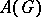 , making the Burnside ring into a pre-
, making the Burnside ring into a pre-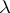 -ring. As a rule this pre-
-ring. As a rule this pre-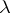 -ring is not a
-ring is not a 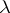 -ring, [a9].
-ring, [a9].
Instead of pre-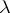 -ring and
-ring and 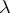 -ring one also finds, respectively, the phrases
-ring one also finds, respectively, the phrases 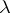 -ring and special
-ring and special 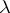 -ring in the literature.
-ring in the literature.
Let 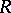 be a pre-
be a pre-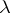 -ring. One defines new operations
-ring. One defines new operations 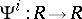 by the formula
by the formula
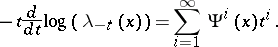 |
These operations are called the Adams operations on the pre-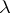 -ring
-ring 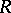 . They were introduced in the case
. They were introduced in the case 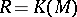 by J.F. Adams ([a10]).
by J.F. Adams ([a10]).
The Adams operations satisfy
iv) 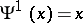 ;
;
v) 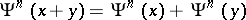 .
.
Let 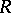 be a torsion-free pre-
be a torsion-free pre-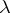 -ring; then
-ring; then 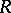 is a
is a 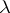 -ring if and only if the Adams operations satisfy in addition
-ring if and only if the Adams operations satisfy in addition
vi) 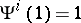 ;
;
vii) 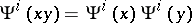 ;
;
viii) 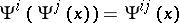 .
.
A ring 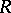 with operations
with operations 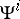 satisfying iv)–viii) is sometimes called a
satisfying iv)–viii) is sometimes called a 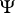 -ring.
-ring.
The ring 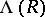 is isomorphic to the ring
is isomorphic to the ring 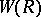 of (big) Witt vectors (cf. (the editorial comments to) Witt vector):
of (big) Witt vectors (cf. (the editorial comments to) Witt vector):
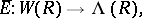 |
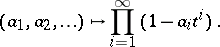 |
Under this isomorphism the Adams operations 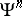 on
on 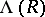 correspond to the Frobenius operations
correspond to the Frobenius operations 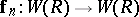 .
.
The 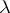 -structures on the rings
-structures on the rings 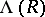 define a functorial morphism of ring-valued functors
define a functorial morphism of ring-valued functors 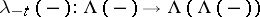 . Together with
. Together with 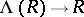 ,
, 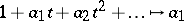 , this defines a co-triple structure on the functor
, this defines a co-triple structure on the functor 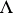 , and the
, and the 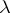 -rings are precisely the co-algebras of this co-triple (cf. Triple).
-rings are precisely the co-algebras of this co-triple (cf. Triple).
Via the isomorphism 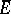 one finds "exponential homomorphisms"
one finds "exponential homomorphisms"
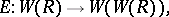 |
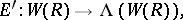 |
which should be seen as (generalizing) the so-called Artin–Hasse exponential ([a11], [a12]).
Let 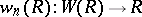 be the ring homomorphism
be the ring homomorphism
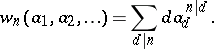 |
Then the Artin–Hasse exponential 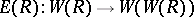 is functorially characterized by
is functorially characterized by
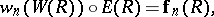 |
where 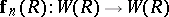 is the Frobenius homomorphism.
is the Frobenius homomorphism.
Let 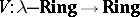 be the forgetful functor. Then the functor
be the forgetful functor. Then the functor 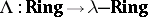 is right adjoint (cf. Adjoint functor) to
is right adjoint (cf. Adjoint functor) to 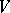 :
:
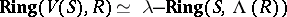 |
(cf. [a5], p. 20).
There are (besides the identity) three natural automorphisms of the Abelian group 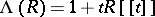 , given by the substitution
, given by the substitution 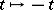 , the "inversion"
, the "inversion" 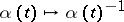 , and the combination of the two. Correspondingly there are four natural ways to introduce a ring structure on
, and the combination of the two. Correspondingly there are four natural ways to introduce a ring structure on 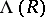 ; the corresponding unit elements are
; the corresponding unit elements are 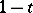 ,
, 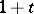 ,
, 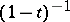 ,
, 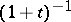 . All four occur in the literature. The most frequently occurring have
. All four occur in the literature. The most frequently occurring have 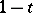 or
or 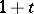 as their unit element — here, in the above,
as their unit element — here, in the above, 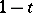 is the unit element —, and
is the unit element —, and 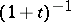 seems to be the most rare case.
seems to be the most rare case.
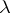 -rings were introduced by A. Grothendieck in an algebraic-geometric setting [a2] and were first used in group representation theory by M.F. Atiyah and D.O. Tall ([a1]).
-rings were introduced by A. Grothendieck in an algebraic-geometric setting [a2] and were first used in group representation theory by M.F. Atiyah and D.O. Tall ([a1]).
In case 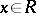 is one-dimensional, i.e.
is one-dimensional, i.e. 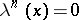 for
for 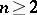 , the terminology derives from the case
, the terminology derives from the case 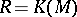 or
or 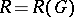 ; one has
; one has 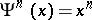 , whence the name power operations for the
, whence the name power operations for the 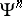 . On the
. On the 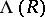 the operations
the operations 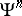 are directly defined by
are directly defined by
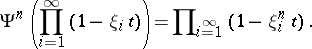 |
References
| [a1] | M.F. Atiyah, D.O. Tall, "Group representations, 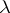 -rings and the -rings and the 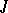 -homomorphism" Topology , 8 (1969) pp. 253–297 MR244387 -homomorphism" Topology , 8 (1969) pp. 253–297 MR244387 |
| [a2] | A. Grothendieck, "La théorie des classes de Chern" Bull. Soc. Math. France , 86 (1958) pp. 137–154 MR0116023 Zbl 0091.33201 |
| [a3] | A. Grothendieck, "Classes de faisceaux et théorème de Riemann–Roch" , Sem. Géom. Algébrique , 6 , Springer (1972) pp. 20–77 Zbl 0229.14008 |
| [a4] | M. Hazewinkel, "Formal groups and applications" , Acad. Press (1978) pp. 144ff MR0506881 MR0463184 Zbl 0454.14020 |
| [a5] | D. Knutson, "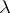 -rings and the representation theory of the symmetric group" , Springer (1974) MR0364425 Zbl 0272.20008 -rings and the representation theory of the symmetric group" , Springer (1974) MR0364425 Zbl 0272.20008 |
| [a6] | P. Berthelot, "Généralités sur les 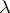 -anneaux" , Sem. Géom. Algébrique , 6 , Springer (1972) pp. 297–365 -anneaux" , Sem. Géom. Algébrique , 6 , Springer (1972) pp. 297–365 |
| [a7] | W. Fulton, S. Lang, "Riemann–Roch algebra" , Springer (1985) MR0801033 Zbl 0579.14011 |
| [a8] | T. tom Dieck, "Transformation groups and representation theory" , Springer (1979) Zbl 0445.57023 |
| [a9] | C. Siebeneicher, " -Ringstrukturen auf dem Burnsidering der Permutationsdarstellungen einer endlichen Gruppe" Math. Z. , 146 (1976) pp. 223–238 MR0390035 Zbl 0306.20011 -Ringstrukturen auf dem Burnsidering der Permutationsdarstellungen einer endlichen Gruppe" Math. Z. , 146 (1976) pp. 223–238 MR0390035 Zbl 0306.20011 |
| [a10] | J.F. Adams, "Vectorfields on spheres" Ann. of Math. , 75 (1962) pp. 603–632 |
| [a11] | M. Hazewinkel, "Twisted Lubin–Tate formal group laws, ramified Witt vectors and (ramified) Artin–Hasse exponentials" Trans. Amer. Math. Soc. , 259 (1980) pp. 47–63 MR0561822 Zbl 0437.13014 |
| [a12] | E. Artin, H. Hasse, "Die beide Ergänzungssätze zum Reciprozitätsgesetz der  -ten Potenzreste im Körper der -ten Potenzreste im Körper der  -ten Einheitswurzeln" Abh. Math. Sem. Univ. Hamburg , 6 (1928) pp. 146–162 -ten Einheitswurzeln" Abh. Math. Sem. Univ. Hamburg , 6 (1928) pp. 146–162 |
| [a13] | G. Whaples, "Generalized local class field theory III: Second form of the existence theorem, structure of analytic groups" Duke Math. J. , 21 (1954) pp. 575–581 MR73645 |
Lambda-ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lambda-ring&oldid=37663