Difference between revisions of "Kowalewski top"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | k1101601.png | ||
| + | $#A+1 = 77 n = 3 | ||
| + | $#C+1 = 77 : ~/encyclopedia/old_files/data/K110/K.1100160 Kowalewski top, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''Kovalevskaya top'' | ''Kovalevskaya top'' | ||
| − | In 1889, S. Kovalevskaya [[#References|[a11]]] solved the following problem: find all rigid bodies, rotating about a fixed point in the presence of gravity, such that the equations of motion are integrable in the sense of Kowalewski. The latter means that the system admits solutions, expressible as [[Laurent series|Laurent series]] in time | + | In 1889, S. Kovalevskaya [[#References|[a11]]] solved the following problem: find all rigid bodies, rotating about a fixed point in the presence of gravity, such that the equations of motion are integrable in the sense of Kowalewski. The latter means that the system admits solutions, expressible as [[Laurent series|Laurent series]] in time $ t $, |
| + | which contain a number of free parameters equal to the number of degrees of freedom minus one; the $ 6 $- | ||
| + | dimensional phase space for such a rigid body is $ { \mathop{\rm SO} } ( 3 ) \times { \mathop{\rm so} } ( 3 ) $. | ||
| + | After the standard reduction to the body coordinates (reduction to the [[Lie algebra|Lie algebra]] $ { \mathop{\rm so} } ( 3 ) $), | ||
| + | for the system to be integrable in the sense of Kowalewski, the Jacobian matrix of the indicial locus (of the equations of motion) must have integer spectrum. This strong condition leads to the following three cases of integrable rotating bodies: i) the Euler top, for which the fixed point and the centre of mass coincide; ii) the Lagrange top, which is an axially-symmetric rigid body, with centre of mass on the axis of symmetry; and iii) the so-called Kowalewski top, which is a solid body rotating about a fixed point such that: | ||
| − | a) its principal moments of inertia | + | a) its principal moments of inertia $ \lambda = ( \lambda _ {1} , \lambda _ {2} , \lambda _ {3} ) $ |
| + | with regard to the fixed point satisfy the relation $ \lambda _ {1} = \lambda _ {2} = 2 \lambda _ {3} $; | ||
| − | b) its centre of mass belongs to the equatorial plane (corresponding to the moment | + | b) its centre of mass belongs to the equatorial plane (corresponding to the moment $ \lambda _ {1} $ |
| + | and $ \lambda _ {2} $) | ||
| + | through the fixed point. The motion (in body coordinates) is governed by the equations | ||
| − | + | $$ | |
| + | {\dot{m} } = ( m \times \lambda m ) + ( \gamma \times l ) , | ||
| + | $$ | ||
| − | + | $$ | |
| + | {\dot \gamma } = \gamma \times \lambda m, | ||
| + | $$ | ||
| − | where | + | where $ m $, |
| + | $ l $ | ||
| + | and $ \gamma $ | ||
| + | denote, respectively, the angular momentum, the centre of mass and the unit vector in the direction of gravity; also, $ \lambda m = ( \lambda _ {1} m _ {1} , \lambda _ {2} m _ {2} , \lambda _ {3} m _ {3} ) $. | ||
| + | Upon appropriate rescaling and picking the axes of inertia in the equatorial plane, one can achieve $ l = ( 2,0,0 ) $ | ||
| + | and $ \lambda m = ( m _ {1} ,m _ {2} ,2m _ {3} ) $. | ||
| + | Besides the Casimir invariants, the angular momentum in the direction of gravity $ Q _ {1} = \langle {m, \gamma } \rangle = A _ {1} $, | ||
| + | the length of the squared gravity axis $ Q _ {2} = | \gamma | ^ {2} = A _ {2} $, | ||
| + | and the conservation of energy $ Q _ {3} = { {\langle {\lambda m,m } \rangle } / 2 } + \langle {l, \gamma } \rangle = { {A _ {3} } / 2 } $, | ||
| + | Kovalevskaya exhibited a $ 4 $ | ||
| + | th invariant, which is quartic, upon giving weight $ 1 $ | ||
| + | to the $ m $' | ||
| + | s and $ 2 $ | ||
| + | to the $ \gamma $' | ||
| + | s: | ||
| − | + | $$ | |
| + | Q _ {4} = \left ( \left ( { | ||
| + | \frac{m _ {1} + im _ {2} }{2} | ||
| + | } \right ) ^ {2} - ( \gamma _ {1} + i \gamma _ {2} ) \right ) \times | ||
| + | $$ | ||
| − | + | $$ | |
| + | \times | ||
| + | \left ( \left ( { | ||
| + | \frac{m _ {1} - im _ {2} }{2} | ||
| + | } \right ) ^ {2} - ( \gamma _ {1} - i \gamma _ {2} ) \right ) = A _ {4} . | ||
| + | $$ | ||
==Algebraic integrability.== | ==Algebraic integrability.== | ||
| − | The motion is "algebraically integrable" in a sense defined by M. Adler and P. van Moerbeke [[#References|[a3]]], [[#References|[a5]]]: for fixed but arbitrary values of the constants of motion, the level surfaces are affine parts | + | The motion is "algebraically integrable" in a sense defined by M. Adler and P. van Moerbeke [[#References|[a3]]], [[#References|[a5]]]: for fixed but arbitrary values of the constants of motion, the level surfaces are affine parts $ {\mathcal A} $ |
| + | of Abelian varieties $ T _ {\mathbf C} ^ {N} $( | ||
| + | complex algebraic tori; cf. [[Algebraic torus|Algebraic torus]]). For the Kowalewski top, the level surfaces $ \cap _ {i = 1 } ^ {4} \{ Q _ {i} = A _ {i} \} $ | ||
| + | are affine parts $ {\mathcal A} $ | ||
| + | of Abelian surfaces $ T _ {\mathbf C} ^ {2} $ | ||
| + | of polarization $ ( 2,4 ) $( | ||
| + | cf. [[Polarized algebraic variety|Polarized algebraic variety]]), and the complement $ T _ {\mathbf C} ^ {2} \backslash {\mathcal A} $ | ||
| + | is a union of two ample divisors (curves) of genus $ 3 $, | ||
| + | each of them being a doubly ramified (in $ 4 $ | ||
| + | points) cover of an [[Elliptic curve|elliptic curve]]. The Kowalewski system then "linearizes" on these Abelian varieties, and the motion can be written in terms of Abelian integrals (quadratures; cf. also [[Abelian integral|Abelian integral]]), involving an intricate change of variables, governed by the algebraic geometry above; see [[#References|[a13]]] and for the quadratures [[#References|[a9]]]. A birational mapping transforms Kowalewski's motion into a [[Geodesic flow|geodesic flow]] on $ { \mathop{\rm SO} } ( 4 ) $ | ||
| + | for the Manakov metric [[#References|[a4]]]. | ||
==Lax pairs.== | ==Lax pairs.== | ||
The Kowalewski top equations can be expressed as a Lax pair (see [[#References|[a8]]]) of the following form: | The Kowalewski top equations can be expressed as a Lax pair (see [[#References|[a8]]]) of the following form: | ||
| − | + | $$ \tag{a1 } | |
| + | - { | ||
| + | \frac{i}{2} | ||
| + | } ( L _ {- 1 } h ^ {- 1 } + L _ {0} + L _ {1} h ) ^ \bullet = | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | = | ||
| + | [ L _ {- 1 } h ^ {- 1 } + L _ {0} + L _ {1} h, B _ {0} - L _ {1} h ] , | ||
| + | $$ | ||
| − | + | where $ h $ | |
| + | is an indeterminate, and where the $ L _ {i} $ | ||
| + | and $ B _ {0} $ | ||
| + | are $ { \mathop{\rm sl} } ( 4 ) $ | ||
| + | matrices, defined below. The motion then linearizes on the Jacobian of the corresponding spectral curve $ { \mathop{\rm det} } ( L _ {- 1 } h ^ {- 1 } + L _ {0} + L _ {1} h - zI ) = 0 $, | ||
| + | which is a double cover (of genus $ 5 $) | ||
| + | of a [[Hyper-elliptic curve|hyper-elliptic curve]] of genus $ 2 $, | ||
| + | ramified at $ 4 $ | ||
| + | points. The matrices in (a1) are given by: | ||
| − | + | $$ | |
| + | L _ {- 1 } = \left ( | ||
| − | + | \begin{array}{cccc} | |
| + | 0 &y _ {2} - x _ {2} ^ {2} & 0 &- y _ {3} \\ | ||
| + | x _ {1} ^ {2} - y _ {1} & 0 &y _ {3} & 0 \\ | ||
| + | 0 &- y _ {3} & 0 &x _ {1} ^ {2} - y _ {1} \\ | ||
| + | y _ {3} & 0 &y _ {2} - x _ {2} ^ {2} & 0 \\ | ||
| + | \end{array} | ||
| + | |||
| + | \right ) , | ||
| + | $$ | ||
| − | + | $$ | |
| + | L _ {0} = \left ( | ||
| − | + | \begin{array}{cccc} | |
| + | 0 & 0 &- x _ {2} & 0 \\ | ||
| + | 0 & 0 & 0 &x _ {1} \\ | ||
| + | - x _ {1} & 0 &- x _ {3} & 0 \\ | ||
| + | 0 &x _ {2} & 0 &x _ {3} \\ | ||
| + | \end{array} | ||
| − | + | \right ) , | |
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | L _ {1} = \left ( | ||
| + | |||
| + | \begin{array}{cccc} | ||
| + | 0 & 0 & 0 & 0 \\ | ||
| + | 0 & 0 & 0 & 0 \\ | ||
| + | 0 & 0 & 0 &- 1 \\ | ||
| + | 0 & 0 & 1 & 0 \\ | ||
| + | \end{array} | ||
| + | |||
| + | \right ) , | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | B _ {0} = \left ( | ||
| + | |||
| + | \begin{array}{cccc} | ||
| + | - x _ {3} & 0 &x _ {2} & 0 \\ | ||
| + | 0 &x _ {3} & 0 &- x _ {1} \\ | ||
| + | x _ {1} & 0 &x _ {3} & 0 \\ | ||
| + | 0 &- x _ {2} & 0 &- x _ {3} \\ | ||
| + | \end{array} | ||
| + | |||
| + | \right ) , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | ( x _ {1} ,x _ {2} ,x _ {3} ,y _ {1} ,y _ {2} ,y _ {3} ) = | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | = | ||
| + | \left ( { | ||
| + | \frac{m _ {1} + im _ {2} }{2} | ||
| + | } , { | ||
| + | \frac{m _ {1} - im _ {2} }{2} | ||
| + | } ,m _ {3} , \right . \left . x _ {1} ^ {2} - ( \gamma _ {1} + i \gamma _ {2} ) ,x _ {2} ^ {2} - ( \gamma _ {1} - i \gamma _ {2} ) , \gamma _ {3} \right ) . | ||
| + | $$ | ||
| + | |||
| + | Such Lax pairs arise in the context of Kostant–Kirillov–Souriau orbits, for Lie algebra splittings into two Lie subalgebras, as summarized by the Adler–Kostant–Symes theorem [[#References|[a1]]], [[#References|[a2]]]. A variation of the latter theorem was applied in [[#References|[a8]]] to a loop algebra $ {\mathcal L} $( | ||
| + | cf. also [[Loop|Loop]]) with a new bracket $ [ x,y ] _ {R} $, | ||
| + | constructed as follows: consider the [[Lie algebra|Lie algebra]] $ g = { \mathop{\rm so} } ( p,q ) $ | ||
| + | and its decomposition $ g = g _ {0} + g _ {1} $ | ||
| + | into even and odd subspaces for the automorphism $ \nu : M \rightarrow {- M ^ \top } $. | ||
| + | Then $ g _ {0} = { \mathop{\rm so} } ( p ) + { \mathop{\rm so} } ( q ) $. | ||
| + | From this, construct the twisted loop algebra $ {\mathcal L} = {\mathcal L} ( g, \nu ) = \oplus h ^ {i} g _ {i} ( { \mathop{\rm mod} } 1 ) $, | ||
| + | together with its splitting and dual splitting, for a non-degenerate ad-invariant pairing: | ||
| + | |||
| + | $$ | ||
| + | {\mathcal L} = {\mathcal L} _ {+} + {\mathcal L} _ {-} = \left \{ \sum _ {n \geq 0 } M _ {n} h ^ {n} \right \} + \left \{ \sum _ {n < 0 } M _ {n} h ^ {n} \right \} | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | {\mathcal L} ^ {*} = {\mathcal L} _ {+} ^ \perp + {\mathcal L} _ {-} ^ \perp = \left \{ \sum _ {n \geq 1 } M _ {n} h ^ {n} \right \} + \left \{ \sum _ {n \leq 0 } M _ {n} h ^ {n} \right \} . | ||
| + | $$ | ||
| − | + | For the Kowalewski top, pick $ g = { \mathop{\rm so} } ( 3,2 ) $, | |
| + | viewed as a $ 10 $- | ||
| + | dimensional subspace of the $ 15 $- | ||
| + | dimensional $ { \mathop{\rm so} } ( 3,3 ) \simeq { \mathop{\rm sl} } ( 4 ) $. | ||
| + | After conjugation by a constant matrix, the Lax pair has the form (a1). | ||
| − | + | Another Lax pair mentioned in [[#References|[a4]]] and, in a slight variation, in [[#References|[a12]]] is based on the following idea: the birational mapping, mentioned above, from the Kowalewski top to the geodesic flow on $ { \mathop{\rm SO} } ( 4 ) $ | |
| + | for the Manakov metric leads to the following Lax pair: | ||
| − | + | $$ \tag{a2 } | |
| + | L _ {h} ^ \bullet = [ L _ {h} ,B _ {h} ] , | ||
| + | $$ | ||
| − | + | and the motion linearizes on the Jacobian of the spectral curve $ { \mathop{\rm det} } ( L _ {h} - zI ) = 0 $, | |
| + | which is Kowalewski's original hyper-elliptic curve. In (a2), | ||
| − | + | $$ | |
| + | L _ {h} = ( M + I ) ( v - v ^ \sigma ) \otimes | ||
| + | $$ | ||
| − | + | $$ | |
| + | \otimes | ||
| + | ( v - v ^ \sigma ) + h ( v + v ^ \sigma ) ^ \wedge + Ih ^ {2} , | ||
| + | $$ | ||
| − | + | $$ | |
| + | B _ {h} = ( M + I ) ( v + v ^ \sigma ) ^ \wedge + Ih ^ {2} , | ||
| + | $$ | ||
| − | + | $$ | |
| + | M = { | ||
| + | \frac{1}{2} | ||
| + | } \left ( | ||
| − | + | \begin{array}{ccc} | |
| + | A _ {3} - 1 &- A _ {2} &i ( A _ {3} + 1 ) \\ | ||
| + | - A _ {2} &A _ {1} &- iA _ {2} \\ | ||
| + | i ( A _ {3} + 1 ) &- iA _ {2} &- ( A _ {3} - 1 ) \\ | ||
| + | \end{array} | ||
| − | + | \right ) , | |
| + | $$ | ||
| − | + | $$ | |
| + | v = - { | ||
| + | \frac{1}{2p } | ||
| + | } ( ( x _ {2} ^ {2} - 1 ) , - 2x _ {2} ,i ( x _ {2} ^ {2} + 1 ) ) , | ||
| + | $$ | ||
| − | + | $$ | |
| + | p = - y _ {2} y _ {3} - x _ {2} x _ {3} + x _ {1} x _ {3} y _ {2} + y _ {3} , | ||
| + | $$ | ||
| − | + | $$ | |
| + | \sigma : {( x _ {1} ,x _ {2} ,x _ {3} ,y _ {1} ,y _ {2} ,y _ {3} ) } \rightarrow {( x _ {2} ,x _ {1} , - x _ {3} ,y _ {1} ,y _ {2} , - y _ {3} ) } , | ||
| + | $$ | ||
| − | + | $$ | |
| + | \wedge : {\mathbf R ^ {3} } \rightarrow { { \mathop{\rm so} } ( 3 ) } , | ||
| + | $$ | ||
| − | + | $$ | |
| + | ( a,b,c ) \rightarrow \left ( | ||
| − | + | \begin{array}{ccc} | |
| + | 0 &- c & b \\ | ||
| + | c & 0 &- a \\ | ||
| + | - b & a & 0 \\ | ||
| + | \end{array} | ||
| − | + | \right ) . | |
| + | $$ | ||
See also [[Goryachev–Chaplygin top|Goryachev–Chaplygin top]]. | See also [[Goryachev–Chaplygin top|Goryachev–Chaplygin top]]. | ||
Latest revision as of 22:15, 5 June 2020
Kovalevskaya top
In 1889, S. Kovalevskaya [a11] solved the following problem: find all rigid bodies, rotating about a fixed point in the presence of gravity, such that the equations of motion are integrable in the sense of Kowalewski. The latter means that the system admits solutions, expressible as Laurent series in time $ t $, which contain a number of free parameters equal to the number of degrees of freedom minus one; the $ 6 $- dimensional phase space for such a rigid body is $ { \mathop{\rm SO} } ( 3 ) \times { \mathop{\rm so} } ( 3 ) $. After the standard reduction to the body coordinates (reduction to the Lie algebra $ { \mathop{\rm so} } ( 3 ) $), for the system to be integrable in the sense of Kowalewski, the Jacobian matrix of the indicial locus (of the equations of motion) must have integer spectrum. This strong condition leads to the following three cases of integrable rotating bodies: i) the Euler top, for which the fixed point and the centre of mass coincide; ii) the Lagrange top, which is an axially-symmetric rigid body, with centre of mass on the axis of symmetry; and iii) the so-called Kowalewski top, which is a solid body rotating about a fixed point such that:
a) its principal moments of inertia $ \lambda = ( \lambda _ {1} , \lambda _ {2} , \lambda _ {3} ) $ with regard to the fixed point satisfy the relation $ \lambda _ {1} = \lambda _ {2} = 2 \lambda _ {3} $;
b) its centre of mass belongs to the equatorial plane (corresponding to the moment $ \lambda _ {1} $ and $ \lambda _ {2} $) through the fixed point. The motion (in body coordinates) is governed by the equations
$$ {\dot{m} } = ( m \times \lambda m ) + ( \gamma \times l ) , $$
$$ {\dot \gamma } = \gamma \times \lambda m, $$
where $ m $, $ l $ and $ \gamma $ denote, respectively, the angular momentum, the centre of mass and the unit vector in the direction of gravity; also, $ \lambda m = ( \lambda _ {1} m _ {1} , \lambda _ {2} m _ {2} , \lambda _ {3} m _ {3} ) $. Upon appropriate rescaling and picking the axes of inertia in the equatorial plane, one can achieve $ l = ( 2,0,0 ) $ and $ \lambda m = ( m _ {1} ,m _ {2} ,2m _ {3} ) $. Besides the Casimir invariants, the angular momentum in the direction of gravity $ Q _ {1} = \langle {m, \gamma } \rangle = A _ {1} $, the length of the squared gravity axis $ Q _ {2} = | \gamma | ^ {2} = A _ {2} $, and the conservation of energy $ Q _ {3} = { {\langle {\lambda m,m } \rangle } / 2 } + \langle {l, \gamma } \rangle = { {A _ {3} } / 2 } $, Kovalevskaya exhibited a $ 4 $ th invariant, which is quartic, upon giving weight $ 1 $ to the $ m $' s and $ 2 $ to the $ \gamma $' s:
$$ Q _ {4} = \left ( \left ( { \frac{m _ {1} + im _ {2} }{2} } \right ) ^ {2} - ( \gamma _ {1} + i \gamma _ {2} ) \right ) \times $$
$$ \times \left ( \left ( { \frac{m _ {1} - im _ {2} }{2} } \right ) ^ {2} - ( \gamma _ {1} - i \gamma _ {2} ) \right ) = A _ {4} . $$
Algebraic integrability.
The motion is "algebraically integrable" in a sense defined by M. Adler and P. van Moerbeke [a3], [a5]: for fixed but arbitrary values of the constants of motion, the level surfaces are affine parts $ {\mathcal A} $ of Abelian varieties $ T _ {\mathbf C} ^ {N} $( complex algebraic tori; cf. Algebraic torus). For the Kowalewski top, the level surfaces $ \cap _ {i = 1 } ^ {4} \{ Q _ {i} = A _ {i} \} $ are affine parts $ {\mathcal A} $ of Abelian surfaces $ T _ {\mathbf C} ^ {2} $ of polarization $ ( 2,4 ) $( cf. Polarized algebraic variety), and the complement $ T _ {\mathbf C} ^ {2} \backslash {\mathcal A} $ is a union of two ample divisors (curves) of genus $ 3 $, each of them being a doubly ramified (in $ 4 $ points) cover of an elliptic curve. The Kowalewski system then "linearizes" on these Abelian varieties, and the motion can be written in terms of Abelian integrals (quadratures; cf. also Abelian integral), involving an intricate change of variables, governed by the algebraic geometry above; see [a13] and for the quadratures [a9]. A birational mapping transforms Kowalewski's motion into a geodesic flow on $ { \mathop{\rm SO} } ( 4 ) $ for the Manakov metric [a4].
Lax pairs.
The Kowalewski top equations can be expressed as a Lax pair (see [a8]) of the following form:
$$ \tag{a1 } - { \frac{i}{2} } ( L _ {- 1 } h ^ {- 1 } + L _ {0} + L _ {1} h ) ^ \bullet = $$
$$ = [ L _ {- 1 } h ^ {- 1 } + L _ {0} + L _ {1} h, B _ {0} - L _ {1} h ] , $$
where $ h $ is an indeterminate, and where the $ L _ {i} $ and $ B _ {0} $ are $ { \mathop{\rm sl} } ( 4 ) $ matrices, defined below. The motion then linearizes on the Jacobian of the corresponding spectral curve $ { \mathop{\rm det} } ( L _ {- 1 } h ^ {- 1 } + L _ {0} + L _ {1} h - zI ) = 0 $, which is a double cover (of genus $ 5 $) of a hyper-elliptic curve of genus $ 2 $, ramified at $ 4 $ points. The matrices in (a1) are given by:
$$ L _ {- 1 } = \left ( \begin{array}{cccc} 0 &y _ {2} - x _ {2} ^ {2} & 0 &- y _ {3} \\ x _ {1} ^ {2} - y _ {1} & 0 &y _ {3} & 0 \\ 0 &- y _ {3} & 0 &x _ {1} ^ {2} - y _ {1} \\ y _ {3} & 0 &y _ {2} - x _ {2} ^ {2} & 0 \\ \end{array} \right ) , $$
$$ L _ {0} = \left ( \begin{array}{cccc} 0 & 0 &- x _ {2} & 0 \\ 0 & 0 & 0 &x _ {1} \\ - x _ {1} & 0 &- x _ {3} & 0 \\ 0 &x _ {2} & 0 &x _ {3} \\ \end{array} \right ) , $$
$$ L _ {1} = \left ( \begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 &- 1 \\ 0 & 0 & 1 & 0 \\ \end{array} \right ) , $$
$$ B _ {0} = \left ( \begin{array}{cccc} - x _ {3} & 0 &x _ {2} & 0 \\ 0 &x _ {3} & 0 &- x _ {1} \\ x _ {1} & 0 &x _ {3} & 0 \\ 0 &- x _ {2} & 0 &- x _ {3} \\ \end{array} \right ) , $$
where
$$ ( x _ {1} ,x _ {2} ,x _ {3} ,y _ {1} ,y _ {2} ,y _ {3} ) = $$
$$ = \left ( { \frac{m _ {1} + im _ {2} }{2} } , { \frac{m _ {1} - im _ {2} }{2} } ,m _ {3} , \right . \left . x _ {1} ^ {2} - ( \gamma _ {1} + i \gamma _ {2} ) ,x _ {2} ^ {2} - ( \gamma _ {1} - i \gamma _ {2} ) , \gamma _ {3} \right ) . $$
Such Lax pairs arise in the context of Kostant–Kirillov–Souriau orbits, for Lie algebra splittings into two Lie subalgebras, as summarized by the Adler–Kostant–Symes theorem [a1], [a2]. A variation of the latter theorem was applied in [a8] to a loop algebra $ {\mathcal L} $( cf. also Loop) with a new bracket $ [ x,y ] _ {R} $, constructed as follows: consider the Lie algebra $ g = { \mathop{\rm so} } ( p,q ) $ and its decomposition $ g = g _ {0} + g _ {1} $ into even and odd subspaces for the automorphism $ \nu : M \rightarrow {- M ^ \top } $. Then $ g _ {0} = { \mathop{\rm so} } ( p ) + { \mathop{\rm so} } ( q ) $. From this, construct the twisted loop algebra $ {\mathcal L} = {\mathcal L} ( g, \nu ) = \oplus h ^ {i} g _ {i} ( { \mathop{\rm mod} } 1 ) $, together with its splitting and dual splitting, for a non-degenerate ad-invariant pairing:
$$ {\mathcal L} = {\mathcal L} _ {+} + {\mathcal L} _ {-} = \left \{ \sum _ {n \geq 0 } M _ {n} h ^ {n} \right \} + \left \{ \sum _ {n < 0 } M _ {n} h ^ {n} \right \} $$
$$ {\mathcal L} ^ {*} = {\mathcal L} _ {+} ^ \perp + {\mathcal L} _ {-} ^ \perp = \left \{ \sum _ {n \geq 1 } M _ {n} h ^ {n} \right \} + \left \{ \sum _ {n \leq 0 } M _ {n} h ^ {n} \right \} . $$
For the Kowalewski top, pick $ g = { \mathop{\rm so} } ( 3,2 ) $, viewed as a $ 10 $- dimensional subspace of the $ 15 $- dimensional $ { \mathop{\rm so} } ( 3,3 ) \simeq { \mathop{\rm sl} } ( 4 ) $. After conjugation by a constant matrix, the Lax pair has the form (a1).
Another Lax pair mentioned in [a4] and, in a slight variation, in [a12] is based on the following idea: the birational mapping, mentioned above, from the Kowalewski top to the geodesic flow on $ { \mathop{\rm SO} } ( 4 ) $ for the Manakov metric leads to the following Lax pair:
$$ \tag{a2 } L _ {h} ^ \bullet = [ L _ {h} ,B _ {h} ] , $$
and the motion linearizes on the Jacobian of the spectral curve $ { \mathop{\rm det} } ( L _ {h} - zI ) = 0 $, which is Kowalewski's original hyper-elliptic curve. In (a2),
$$ L _ {h} = ( M + I ) ( v - v ^ \sigma ) \otimes $$
$$ \otimes ( v - v ^ \sigma ) + h ( v + v ^ \sigma ) ^ \wedge + Ih ^ {2} , $$
$$ B _ {h} = ( M + I ) ( v + v ^ \sigma ) ^ \wedge + Ih ^ {2} , $$
$$ M = { \frac{1}{2} } \left ( \begin{array}{ccc} A _ {3} - 1 &- A _ {2} &i ( A _ {3} + 1 ) \\ - A _ {2} &A _ {1} &- iA _ {2} \\ i ( A _ {3} + 1 ) &- iA _ {2} &- ( A _ {3} - 1 ) \\ \end{array} \right ) , $$
$$ v = - { \frac{1}{2p } } ( ( x _ {2} ^ {2} - 1 ) , - 2x _ {2} ,i ( x _ {2} ^ {2} + 1 ) ) , $$
$$ p = - y _ {2} y _ {3} - x _ {2} x _ {3} + x _ {1} x _ {3} y _ {2} + y _ {3} , $$
$$ \sigma : {( x _ {1} ,x _ {2} ,x _ {3} ,y _ {1} ,y _ {2} ,y _ {3} ) } \rightarrow {( x _ {2} ,x _ {1} , - x _ {3} ,y _ {1} ,y _ {2} , - y _ {3} ) } , $$
$$ \wedge : {\mathbf R ^ {3} } \rightarrow { { \mathop{\rm so} } ( 3 ) } , $$
$$ ( a,b,c ) \rightarrow \left ( \begin{array}{ccc} 0 &- c & b \\ c & 0 &- a \\ - b & a & 0 \\ \end{array} \right ) . $$
See also Goryachev–Chaplygin top.
References
| [a1] | M. Adler, "On a trace functional for formal pseudodifferential operators and the symplectic structure for the Korteweg–de Vries type equations" Invent. Math. , 50 (1979) pp. 451–500 |
| [a2] | M. Adler, P. van Moerbeke, "Completely integrable systems, Euclidean Lie algebras and curves; Linearization of Hamiltonian Systems, Jacobi varieties and representation theory" Adv. Math. , 38 (1980) pp. 267–317;318–379 MR0597729 Zbl 0455.58017 |
| [a3] | M. Adler, P. van Moerbeke, "The algebraic integrability of geodesic flow on 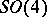 " Invent. Math. , 67 (1982) pp. 297–331 MR0665159 Zbl 0539.58012 " Invent. Math. , 67 (1982) pp. 297–331 MR0665159 Zbl 0539.58012 |
| [a4] | M. Adler, P. van Moerbeke, "The Kowalevski and Hénon–Heiles motions as Manakov geodesic flows on 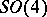 - a two-dimensional family of Lax pairs" Comm. Math. Phys. , 113 (1988) pp. 659–700 - a two-dimensional family of Lax pairs" Comm. Math. Phys. , 113 (1988) pp. 659–700 |
| [a5] | M. Adler, P. van Moerbeke, "The complex geometry of the Kowalevski–Painlevé analysis" Invent. Math. , 97 (1989) pp. 3–51 |
| [a6] | A.G. Reyman, M.A. Semenov-Tian-Shanski, "Reduction of Hamiltonian systems, affine Lie algebras and Lax equations I" Invent. Math. , 54 (1979) pp. 81–100 MR549548 |
| [a7] | A.G. Reyman, M.A. Semenov-Tian-Shanski, "Reduction of Hamiltonian systems, affine Lie algebras and Lax equations II" Invent. Math. , 63 (1981) pp. 423–432 MR0620678 |
| [a8] | A.I. Bobenko, A.G. Reyman, M.A. Semenov-Tian-Shansky, "The Kowalevski top 9 years later: A Lax pair, generalizations and explicit solutions" Comm. Math. Phys. , 122 (1989) pp. 321–354 |
| [a9] | P. Vanhaecke, "Linearising two-dimensional integrable systems and the construction of angle-action variables" Math. Z. , 211 (1992) pp. 265–313 |
| [a10] | V.V. Golubev, "Lectures on the integration of equations of motions of a heavy solid about a fixed point" , Gostekhizdat (1953) (English translation by the Israeli information agency) |
| [a11] | S. Kowalewski, "Sur le problème de la rotation d'un corps solide autour d'un point fixe" Acta Math. , 14 (1889) pp. 81–93 |
| [a12] | L. Haine, E. Horozov, "A Lax pair for Kowalevski's top" Physica D , 29 (1987) pp. 173–180 MR923889 |
| [a13] | E. Horozov, P. van Moerbeke, "The full geometry of Kowalevski's top and 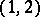 -abelian surfaces" Comm. Pure Appl. Math , 42 (1989) pp. 357–407 -abelian surfaces" Comm. Pure Appl. Math , 42 (1989) pp. 357–407 |
Kowalewski top. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kowalewski_top&oldid=47524