Kodaira theorem
Kodaira's vanishing theorem
A theorem on the vanishing of the cohomology groups 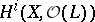 ,
,  , where
, where 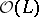 is the sheaf of holomorphic sections of the negative vector bundle
is the sheaf of holomorphic sections of the negative vector bundle 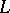 of rank
of rank 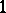 on a compact complex manifold
on a compact complex manifold 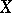 . An equivalent statement of Kodaira's vanishing theorem is that
. An equivalent statement of Kodaira's vanishing theorem is that
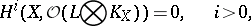 |
for any positive vector bundle of rank 1 (here 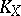 denotes the canonical line bundle on
denotes the canonical line bundle on 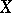 ). In terms of divisors (cf. Divisor) Kodaira's vanishing theorem is stated as the equation
). In terms of divisors (cf. Divisor) Kodaira's vanishing theorem is stated as the equation 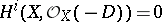 for
for  and any divisor
and any divisor 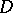 such that for some
such that for some 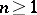 ,
, 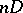 is a hyperplane section in some projective imbedding of
is a hyperplane section in some projective imbedding of 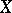 .
.
The theorem was proved by transcendental methods by K. Kodaira [1] (see also [2]) as a generalization to arbitrary dimension of the classical theorem on the regularity of an adjoint system on an algebraic surface. There exists an example of a normal algebraic surface over a field of positive characteristic for which Kodaira's vanishing theorem is false [4].
Kodaira's theorem also holds for holomorphic vector bundles of arbitrary rank that are negative in the sense of J. Nakano. The following result is also a generalization of Kodaira's theorem:
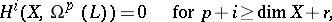 |
where 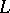 is a weakly-positive vector bundle of rank
is a weakly-positive vector bundle of rank  on the compact complex manifold
on the compact complex manifold 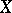 , and
, and 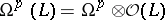 is the sheaf of holomorphic forms (cf. Holomorphic form) of degree
is the sheaf of holomorphic forms (cf. Holomorphic form) of degree 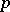 with values in
with values in 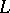 . For weakly-negative vector bundles
. For weakly-negative vector bundles 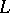 , vanishing takes place when
, vanishing takes place when 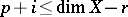 . Analogues of these theorems have been obtained for weakly-complete manifolds
. Analogues of these theorems have been obtained for weakly-complete manifolds 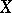 , that is, manifolds admitting a smooth pluriharmonic function
, that is, manifolds admitting a smooth pluriharmonic function  such that the set
such that the set 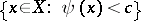 is relatively compact in
is relatively compact in 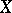 for all
for all 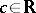 , and for compact complex spaces
, and for compact complex spaces 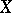 having
having 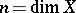 algebraically-independent meromorphic functions [5].
algebraically-independent meromorphic functions [5].
References
| [1] | K. Kodaira, "On a differential geometric method in the theory of analytic stacks" Proc. Nat. Acad. Sci. USA , 39 (1953) pp. 1268–1273 |
| [2] | R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980) |
| [3] | D. Mumford, "Pathologies III" Amer. J. Math. , 89 : 1 (1967) pp. 94–104 |
| [4] | O. Zariski, "Algebraic surfaces" , Springer (1971) |
| [5] | A.L. Onishchik, "Pseudoconvexity in the theory of complex spaces" J. Soviet Math. , 14 : 4 (1980) pp. 1363–1407 Itogi Nauk. Algebra Topol. Geom. , 15 (1977) pp. 93–171 |
Comments
Counterexamples to Kodaira's theorem for non-singular varieties over a field of positive characteristic were given by M. Raynaud [a1]. There exists a much stronger version of Kodaira's theorem, due to E. Viehweg and Y. Kawamata [a2].
Recently, many generalizations of Kodaira vanishing have been found, see [a3].
References
| [a1] | M. Raynaud, "Contre-example du "vanishing theorem" en caractéristique 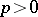 " K.G. Ramanathan (ed.) , C.P. Ramanujam, a tribute , Springer (1978) pp. 273–278 " K.G. Ramanathan (ed.) , C.P. Ramanujam, a tribute , Springer (1978) pp. 273–278 |
| [a2] | E. Viehweg, "Vanishing theorems and positivity in algebraic fibre spaces" , Proc. Internat. Congress Mathematicians (Berkeley, 1986) , 1 , Amer. Math. Soc. (1987) pp. 682–688 |
| [a3] | J. Kollar, "Vanishing theorems for cohomology groups" S.J. Bloch (ed.) , Algebraic geometry (Bowdoin, 1985) , Proc. Symp. Pure Math. , 46 : 2 , Amer. Math. Soc. (1987) pp. 233–243 |
Kodaira theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kodaira_theorem&oldid=13756