K-theory
A part of algebraic topology that studies properties of vector bundles by algebraic and topological methods. As opposed to algebraic  -theory, it is sometimes called topological
-theory, it is sometimes called topological 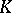 -theory. In a wide sense, the term "K-theory" is used to denote the branch of mathematics that includes algebraic
-theory. In a wide sense, the term "K-theory" is used to denote the branch of mathematics that includes algebraic 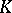 -theory and topological
-theory and topological  -theory, and it is characterized by specific algebraic and topological methods of investigation, which are called methods of
-theory, and it is characterized by specific algebraic and topological methods of investigation, which are called methods of  -theory. In the narrow sense,
-theory. In the narrow sense,  -theory is the generalized cohomology theory (cf. Generalized cohomology theories) generated by the category of vector bundles (cf. Vector bundle).
-theory is the generalized cohomology theory (cf. Generalized cohomology theories) generated by the category of vector bundles (cf. Vector bundle).
The source of  -theory is to be found in the skew-vector products (bundles) studied in algebraic topology, as well as in their numerous homotopic and algebraic properties. The most important properties of bundles and of concepts used in
-theory is to be found in the skew-vector products (bundles) studied in algebraic topology, as well as in their numerous homotopic and algebraic properties. The most important properties of bundles and of concepts used in 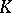 -theory are the properties of characteristic classes (cf. Characteristic class) of bundles, of classifying spaces (cf. Classifying space), of algebraic operations with bundles (direct sums, tensor products, exterior degrees), and of the inverse image of a bundle. A second source of
-theory are the properties of characteristic classes (cf. Characteristic class) of bundles, of classifying spaces (cf. Classifying space), of algebraic operations with bundles (direct sums, tensor products, exterior degrees), and of the inverse image of a bundle. A second source of 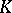 -theory is the connection with algebraic
-theory is the connection with algebraic 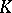 -theory, which consists of the fact that the space of continuous sections of a vector bundle can be regarded as a module over the algebra of continuous functions, which turns out to be a projective module.
-theory, which consists of the fact that the space of continuous sections of a vector bundle can be regarded as a module over the algebra of continuous functions, which turns out to be a projective module.
In analogy with 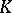 -functors in algebraic
-functors in algebraic 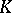 -theory, the groups
-theory, the groups 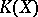 were defined as the Grothendieck groups (cf. Grothendieck group) of the category of vector bundles with
were defined as the Grothendieck groups (cf. Grothendieck group) of the category of vector bundles with 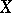 as base. Using the concept of an induced fibre bundle, the groups
as base. Using the concept of an induced fibre bundle, the groups 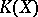 are completed to define a functor from the category of topological spaces into the category of Abelian groups. Usually a
are completed to define a functor from the category of topological spaces into the category of Abelian groups. Usually a 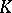 -functor is studied not on the whole category of topological spaces, but on smaller subcategories. The category most often used is that of cellular spaces (complexes, cf. CW-complex). The definition of a
-functor is studied not on the whole category of topological spaces, but on smaller subcategories. The category most often used is that of cellular spaces (complexes, cf. CW-complex). The definition of a 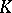 -functor is extended to the category of pointed topological spaces and pairs of topological spaces and yields the groups
-functor is extended to the category of pointed topological spaces and pairs of topological spaces and yields the groups 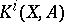 ,
, 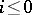 , by putting
, by putting
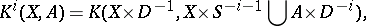 |
where 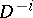 is an
is an  -dimensional disc and
-dimensional disc and 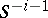 is its boundary. The set of functors
is its boundary. The set of functors 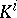 ,
, 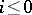 , satisfies the axioms of generalized cohomology theory, which should be altered by taking into account the inequality
, satisfies the axioms of generalized cohomology theory, which should be altered by taking into account the inequality 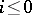 .
.
One distinguishes the  -theory built on the category of real vector bundles (real
-theory built on the category of real vector bundles (real  -theory) from the
-theory) from the 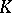 -theory built on complex vector bundles (complex
-theory built on complex vector bundles (complex 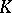 -theory). Other variants of
-theory). Other variants of 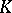 -theory are also studied, which take into account additional structures in certain bundles, for instance equivariant
-theory are also studied, which take into account additional structures in certain bundles, for instance equivariant 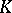 -theory.
-theory.
A property of the group 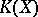 which is important in the construction of generalized cohomology theory is Bott periodicity in complex
which is important in the construction of generalized cohomology theory is Bott periodicity in complex 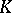 -theory (cf. Bott periodicity theorem). It allows one, in particular, to get rid of the restriction
-theory (cf. Bott periodicity theorem). It allows one, in particular, to get rid of the restriction 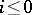 and to transform the functors
and to transform the functors 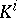 into a
into a 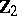 -graded generalized cohomology theory. The fundamental importance of Bott periodicity is due to the vast computational possibilities of the constructed
-graded generalized cohomology theory. The fundamental importance of Bott periodicity is due to the vast computational possibilities of the constructed 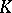 -theory.
-theory.
The computational methods of generalized cohomology theory are applicable to 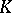 -theory, among them, in particular, the method of spectral sequences (cf. Spectral sequence), allowing one to compute the groups
-theory, among them, in particular, the method of spectral sequences (cf. Spectral sequence), allowing one to compute the groups 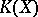 for many classical finite-dimensional and infinite-dimensional spaces. For instance, if
for many classical finite-dimensional and infinite-dimensional spaces. For instance, if  is a complex projective space, then
is a complex projective space, then
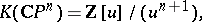 |
where  , and
, and 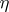 is the one-dimensional canonical bundle over
is the one-dimensional canonical bundle over  .
.
For real 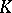 -theory, a
-theory, a 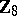 -graded generalized cohomology theory is constructed using the Bott periodicity theorem. Applying supplementary algebraic structures in vector bundles, more general cohomology theories were constructed, organically containing complex, real, and symplectic
-graded generalized cohomology theory is constructed using the Bott periodicity theorem. Applying supplementary algebraic structures in vector bundles, more general cohomology theories were constructed, organically containing complex, real, and symplectic 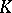 -theories.
-theories.
In the 1960s, with the help of 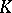 -theory many problems both in topology and in other branches of mathematics were reconsidered. The most important results in
-theory many problems both in topology and in other branches of mathematics were reconsidered. The most important results in 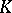 -theory were connected with the systematic study of characteristic classes and of cohomology operations (cf. Cohomology operation) in terms of which theorems about the integral nature for multiplicative genera (analogues of the Riemann–Roch theorem) were proved, and simple and lucid solutions were given for classical problems connected with division algebras and with vector fields on spheres.
-theory were connected with the systematic study of characteristic classes and of cohomology operations (cf. Cohomology operation) in terms of which theorems about the integral nature for multiplicative genera (analogues of the Riemann–Roch theorem) were proved, and simple and lucid solutions were given for classical problems connected with division algebras and with vector fields on spheres.
The methods of 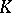 -theory were the origin for the development of many branches of topology, e.g. the theory of bordism. The proof of the Adams' conjecture on the description of the
-theory were the origin for the development of many branches of topology, e.g. the theory of bordism. The proof of the Adams' conjecture on the description of the 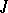 -functor in terms of cohomology operations in
-functor in terms of cohomology operations in 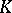 -theory was of fundamental importance for the development of algebraic topology (see [2]).
-theory was of fundamental importance for the development of algebraic topology (see [2]).
Most impressive is the application of methods of 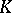 -theory to the problem of computing the indices of elliptic operators. With the help of geometric constructions of vector bundles, far-reaching generalizations were obtained of the concepts of a differential and a pseudo-differential operator, of their symbols, of a Sobolev space, and of elliptic operators and their indices. Also, the Atiyah–Singer formula
-theory to the problem of computing the indices of elliptic operators. With the help of geometric constructions of vector bundles, far-reaching generalizations were obtained of the concepts of a differential and a pseudo-differential operator, of their symbols, of a Sobolev space, and of elliptic operators and their indices. Also, the Atiyah–Singer formula
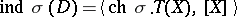 |
was obtained [3]; it describes the index of an elliptic operator with symbol 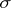 on a compact closed manifold
on a compact closed manifold 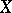 in terms of the Todd class
in terms of the Todd class 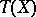 and the Chern character of the operator
and the Chern character of the operator 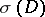 . As corollaries to the Atiyah–Singer formula many special formulas have been obtained for various classes of operators which are most important in geometry, topology and other branches of mathematics. For instance, Hirzebruch's formula expresses the signature of an oriented compact, closed manifold in terms of the characteristic Pontryagin number of this manifold. The Hirzebruch formula itself and its generalizations to non-simply-connected manifolds is applied in differential topology to problems on the classification of smooth structures of manifolds.
. As corollaries to the Atiyah–Singer formula many special formulas have been obtained for various classes of operators which are most important in geometry, topology and other branches of mathematics. For instance, Hirzebruch's formula expresses the signature of an oriented compact, closed manifold in terms of the characteristic Pontryagin number of this manifold. The Hirzebruch formula itself and its generalizations to non-simply-connected manifolds is applied in differential topology to problems on the classification of smooth structures of manifolds.
In the 1970s generalizations of 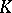 -theory connected with the applications in it of functional-analytic methods and with the adaptation of
-theory connected with the applications in it of functional-analytic methods and with the adaptation of 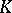 -theory to many problems of topology, geometry and of the theory of differential equations appeared. One of the generalizations consists of the replacement of the category of vector bundles by that of locally trivial fibre bundles (cf. Locally trivial fibre bundle) in which the fibres are finitely-generated modules which are projective over some
-theory to many problems of topology, geometry and of the theory of differential equations appeared. One of the generalizations consists of the replacement of the category of vector bundles by that of locally trivial fibre bundles (cf. Locally trivial fibre bundle) in which the fibres are finitely-generated modules which are projective over some 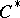 -algebra
-algebra  and the structure groups of which are groups of automorphisms of these modules. Using this class of fibre bundles, non-trivial cohomology invariants were constructed for infinite-dimensional representations of infinite discrete groups
and the structure groups of which are groups of automorphisms of these modules. Using this class of fibre bundles, non-trivial cohomology invariants were constructed for infinite-dimensional representations of infinite discrete groups 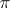 . If a discrete group
. If a discrete group 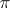 is the fundamental group of a compact manifold admitting a Riemannian metric with non-positive two-dimensional curvature, then the characteristic numbers of the form
is the fundamental group of a compact manifold admitting a Riemannian metric with non-positive two-dimensional curvature, then the characteristic numbers of the form
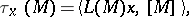 |
that is, the higher signatures, are homology invariants. (Here,  is an arbitrary rational Pontryagin–Hirzebruch class of the manifold
is an arbitrary rational Pontryagin–Hirzebruch class of the manifold 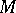 with fundamental group
with fundamental group 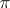 .)
.)
In a wider sense, the methods of  -theory greatly influenced the development of ideas in differential topology. With the help of a combination of algebraic and topological
-theory greatly influenced the development of ideas in differential topology. With the help of a combination of algebraic and topological 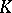 -theories, problems in differential topology were solved about the classification of smooth and of piecewise-linear structures on manifolds, about the homological and topological invariance of the characteristic Pontryagin classes, etc. Methods of
-theories, problems in differential topology were solved about the classification of smooth and of piecewise-linear structures on manifolds, about the homological and topological invariance of the characteristic Pontryagin classes, etc. Methods of 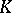 -theory have extensive applications in functional analysis, and in particular in the theory of Banach algebras (cf. Banach algebra).
-theory have extensive applications in functional analysis, and in particular in the theory of Banach algebras (cf. Banach algebra).
References
| [1] | M.F. Atiyah, F. Hirzebruch, "Vector bundles and homogeneous spaces" C.B. Allendoerfer (ed.) , Differential geometry , Proc. Symp. Pure Math. , 3 , Amer. Math. Soc. (1961) pp. 7–38 |
| [2] | D. Sullivan, "Genetics of homotopy theory" Ann. of Math. , 100 (1974) pp. 1–79 |
| [3] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators on compact manifolds" Bull. Amer. Math. Soc. , 69 (1963) pp. 422–433 |
| [4] | N.E. Steenrod, "The topology of fibre bundles" , Princeton Univ. Press (1951) |
| [5] | M.F. Atiyah, "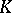 -theory: lectures" , Benjamin (1967) -theory: lectures" , Benjamin (1967) |
| [6] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) |
| [7] | M. Karoubi, "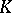 -theory: an introduction" , Springer (1978) (Translated from French) -theory: an introduction" , Springer (1978) (Translated from French) |
Comments
A most useful formula for calculating 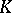 groups is the following. Let
groups is the following. Let 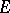 be an
be an  -dimensional vector bundle over
-dimensional vector bundle over  . Denote by
. Denote by 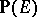 the associated
the associated 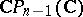 whose fibre over
whose fibre over 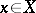 is the
is the 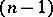 -dimensional projective space of lines in the fibre
-dimensional projective space of lines in the fibre 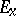 of
of 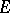 over
over 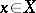 . Over
. Over 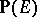 there is the canonical line bundle
there is the canonical line bundle 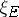 , whose fibre over
, whose fibre over 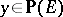 "is" the one-dimensional vector space
"is" the one-dimensional vector space 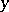 . For
. For 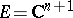 ,
, 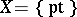 , a one-point space, this is the canonical line bundle over
, a one-point space, this is the canonical line bundle over 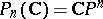 given by
given by 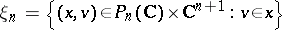 . Let
. Let 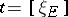 be the class of
be the class of 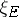 in
in 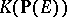 . Then
. Then 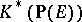 is a free
is a free 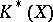 -module with basis
-module with basis  , and
, and 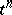 is given by the relation
is given by the relation
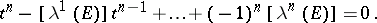 |
In equivariant 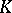 -theory one considers spaces
-theory one considers spaces 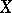 with an action of a (Lie) group
with an action of a (Lie) group  on it. A
on it. A 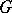 -vector bundle is a vector bundle
-vector bundle is a vector bundle 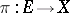 where
where 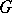 acts on both
acts on both 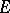 and
and 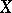 and
and 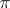 is a mapping of
is a mapping of 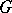 -spaces and
-spaces and 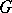 acts on
acts on 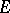 by vector bundle automorphisms (i.e. the restrictions to the fibres
by vector bundle automorphisms (i.e. the restrictions to the fibres 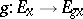 are linear). One has direct sums and tensor products of
are linear). One has direct sums and tensor products of  -vector bundles, yielding a semi-ring of isomorphism classes
-vector bundles, yielding a semi-ring of isomorphism classes 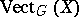 . The equivariant
. The equivariant 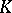 -group
-group 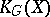 for compact spaces
for compact spaces 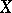 is now the Grothendieck group of
is now the Grothendieck group of 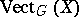 .
.
For 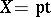 ,
, 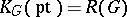 , the representation ring of
, the representation ring of 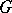 . For a space
. For a space 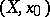 with base point, the reduced groups are defined as
with base point, the reduced groups are defined as 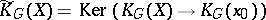 . For locally compact non-compact spaces (with proper
. For locally compact non-compact spaces (with proper 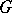 -action),
-action),  , where
, where 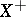 is the one-point compactification of
is the one-point compactification of 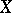 . The higher groups are defined by
. The higher groups are defined by  ,
, 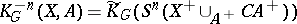 , where
, where 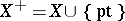 if
if 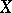 is compact and
is compact and 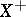 is the one-point compactification of
is the one-point compactification of 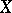 if
if 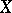 is locally compact but not compact, and where
is locally compact but not compact, and where 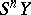 is the
is the  -fold suspension of
-fold suspension of 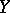 and
and 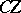 is the cone over
is the cone over 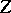 .
.
The 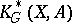 thus defined form again a generalized cohomology theory. Cf. [a1], [a6]–[a9] for more details and applications of
thus defined form again a generalized cohomology theory. Cf. [a1], [a6]–[a9] for more details and applications of 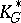 .
.
For a survey of the 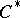 -algebra generalizations and ramifications of
-algebra generalizations and ramifications of 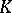 -theory (in particular, for an account of Kasparov
-theory (in particular, for an account of Kasparov 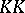 -theory) see [a2]. In addition, an extremely important connection between the topological
-theory) see [a2]. In addition, an extremely important connection between the topological 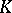 -theory and the algebraic
-theory and the algebraic 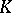 -theory of smooth complex varieties has been found by R.W. Thomason (see [a3], [a4]). Essentially, Thomason showed that the algebraic
-theory of smooth complex varieties has been found by R.W. Thomason (see [a3], [a4]). Essentially, Thomason showed that the algebraic 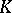 -theory of a smooth variety, when taken with finite coefficients, becomes topological
-theory of a smooth variety, when taken with finite coefficients, becomes topological 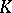 -theory if one localizes in such a way as to impose Bott periodicity. More recently, interrelations have been discovered between the
-theory if one localizes in such a way as to impose Bott periodicity. More recently, interrelations have been discovered between the 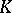 -theory of
-theory of 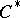 -algebras, Connes' cyclic homology and Waldhausen's algebraic
-algebras, Connes' cyclic homology and Waldhausen's algebraic 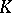 -theory of spaces. For details see [a5], for example.
-theory of spaces. For details see [a5], for example.
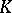 -theory and representation theory are directly related by the fact that for a compact group
-theory and representation theory are directly related by the fact that for a compact group 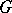 the complex
the complex 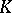 -theory
-theory 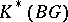 of the classifying space
of the classifying space 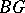 is the completion of the complex representation ring
is the completion of the complex representation ring 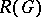 for the topology defined by the augmentation ideal
for the topology defined by the augmentation ideal 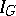 of
of 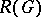 :
:  , [a10].
, [a10].
References
| [a1] | G.B. Segal, "Equivariant 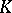 -theory" Publ. Math. IHES , 34 (1968) pp. 129–151 -theory" Publ. Math. IHES , 34 (1968) pp. 129–151 |
| [a2] | B. Blackadar, " -theory for operator algebras" , Springer (1986) -theory for operator algebras" , Springer (1986) |
| [a3] | W.C. Dwyer, E.M. Friedlander, V.P. Snaith, R.W. Thomason, "Algebraic 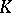 -theory eventually surjects on topological -theory eventually surjects on topological 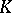 -theory" Invent. Math. , 66 (1982) pp. 481–491 -theory" Invent. Math. , 66 (1982) pp. 481–491 |
| [a4] | R.W. Thomason, "Algebraic 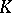 -theory and étale cohomology" Ann. Sci. Ec. Norm. Sup. , 18 (1985) pp. 437–552 -theory and étale cohomology" Ann. Sci. Ec. Norm. Sup. , 18 (1985) pp. 437–552 |
| [a5] | T.G. Goodwillie, "On the general linear group and Hochshild homology" Ann. of Math. (2) , 121 (1985) pp. 383–407 |
| [a6] | T. Petrie, J.D. Randall, "Transformation groups on manifolds" , M. Dekker (1984) pp. 8, 9 |
| [a7] | M.F. Atiyah, G. Segal, "The index of elliptic operators II" Ann. of Math. , 87 (1968) pp. 531–545 |
| [a8] | L. Illusie, "Nombres de Chern et groupes finis" Topology , 7 (1968) pp. 255–270 |
| [a9] | M.F. Atiyah, "Lectures on 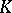 -theory" , Math. Inst. Harvard Univ. (1964) (Mimeographed notes) -theory" , Math. Inst. Harvard Univ. (1964) (Mimeographed notes) |
| [a10] | M.F. Atiyah, G. Segal, "Equivariant 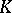 -theory and completion" J. Diff. Geom. , 3 (1969) pp. 1–18 -theory and completion" J. Diff. Geom. , 3 (1969) pp. 1–18 |
K-theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=K-theory&oldid=12407