Difference between revisions of "Jordan triple system"
(Importing text file) |
m (→Examples.: link) |
||
| Line 28: | Line 28: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130060/j13006022.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130060/j13006022.png" /></td> </tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130060/j13006023.png" /> denotes the transpose matrix of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130060/j13006024.png" />. | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130060/j13006023.png" /> denotes the [[transpose matrix]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130060/j13006024.png" />. |
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130060/j13006025.png" /> be a vector space over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130060/j13006026.png" /> equipped with a symmetric bilinear form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130060/j13006027.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130060/j13006028.png" /> is a Jordan triple system with respect to the product | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130060/j13006025.png" /> be a vector space over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130060/j13006026.png" /> equipped with a symmetric bilinear form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130060/j13006027.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130060/j13006028.png" /> is a Jordan triple system with respect to the product | ||
Revision as of 20:04, 21 November 2014
A triple system closely related to Jordan algebras.
A triple system is a vector space  over a field
over a field  together with a
together with a  -trilinear mapping
-trilinear mapping  , called a triple product and usually denoted by
, called a triple product and usually denoted by  (sometimes dropping the commas).
(sometimes dropping the commas).
It is said to be a Jordan triple system if
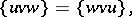 | (a1) |
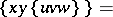 | (a2) |
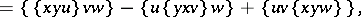 |
with  .
.
From the algebraic viewpoint, a Jordan triple system 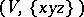 is a Lie triple system with respect to the new triple product
is a Lie triple system with respect to the new triple product
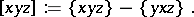 |
This implies that all simple Lie algebras over an algebraically closed field of characteristic zero, except  ,
,  and
and  (cf. also Lie algebra), can be constructed using the standard embedding Lie algebra associated with a Lie triple system via a Lie triple system.
(cf. also Lie algebra), can be constructed using the standard embedding Lie algebra associated with a Lie triple system via a Lie triple system.
From the geometrical viewpoint there is, for example, a correspondence between symmetric  -spaces and compact Jordan triple systems [a3] as well as a correspondence between bounded symmetric domains and Hermitian Jordan triple systems [a2].
-spaces and compact Jordan triple systems [a3] as well as a correspondence between bounded symmetric domains and Hermitian Jordan triple systems [a2].
For superversions of this triple system, see [a5].
Examples.
Let 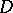 be an associative algebra over
be an associative algebra over 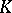 (cf. also Associative rings and algebras) and set
(cf. also Associative rings and algebras) and set  , the
, the  -matrices over
-matrices over  . This vector space
. This vector space  is a Jordan triple system with respect to the product
is a Jordan triple system with respect to the product
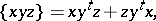 |
where 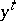 denotes the transpose matrix of
denotes the transpose matrix of 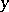 .
.
Let  be a vector space over
be a vector space over  equipped with a symmetric bilinear form
equipped with a symmetric bilinear form  . Then
. Then  is a Jordan triple system with respect to the product
is a Jordan triple system with respect to the product
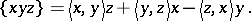 |
Let 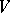 be a commutative Jordan algebra. Then
be a commutative Jordan algebra. Then 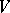 is a Jordan triple system with respect to the product
is a Jordan triple system with respect to the product
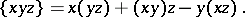 |
Note that a triple system in this sense is completely different from, e.g., the combinatorial notion of a Steiner triple system (cf. also Steiner system).
References
| [a1] | N. Jacobson, "Lie and Jordan triple systems" Amer. J. Math. , 71 (1949) pp. 149–170 |
| [a2] | W. Kaup, "Hermitian Jordan triple systems and the automorphisms of bounded symmetric domains" , Non Associative Algebra and Its Applications (Oviedo, 1993) , Kluwer Acad. Publ. (1994) pp. 204–214 |
| [a3] | O. Loos, "Jordan triple systems, 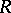 -symmetric spaces, and bounded symmetric domains" Bull. Amer. Math. Soc. , 77 (1971) pp. 558–561 -symmetric spaces, and bounded symmetric domains" Bull. Amer. Math. Soc. , 77 (1971) pp. 558–561 |
| [a4] | E. Nehr, "Jordan triple systems by the graid approach" , Lecture Notes in Mathematics , 1280 , Springer (1987) |
| [a5] | S. Okubo, N. Kamiya, "Jordan–Lie super algebra and Jordan–Lie triple system" J. Algebra , 198 : 2 (1997) pp. 388–411 |
Jordan triple system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jordan_triple_system&oldid=34723