Jacobson radical
of a ring 
The ideal  of an associative ring (cf. Associative rings and algebras)
of an associative ring (cf. Associative rings and algebras)  which satisfies the following two requirements: 1)
which satisfies the following two requirements: 1)  is the largest quasi-regular ideal in
is the largest quasi-regular ideal in  (a ring
(a ring  is called quasi-regular if the equation
is called quasi-regular if the equation  is solvable for any of its elements
is solvable for any of its elements  ); and 2) the quotient ring
); and 2) the quotient ring  contains no non-zero quasi-regular ideals. The radical was introduced and studied in detail in 1945 by N. Jacobson [1].
contains no non-zero quasi-regular ideals. The radical was introduced and studied in detail in 1945 by N. Jacobson [1].
The Jacobson radical always exists and may be characterized in very many ways: 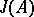 is the intersection of the kernels of all irreducible representations of the ring
is the intersection of the kernels of all irreducible representations of the ring  ; it is the intersection of all modular maximal right ideals (cf. Modular ideal); it is the intersection of all modular maximal left ideals; it contains all quasi-regular one-sided ideals; it contains all one-sided nil ideals; etc. If
; it is the intersection of all modular maximal right ideals (cf. Modular ideal); it is the intersection of all modular maximal left ideals; it contains all quasi-regular one-sided ideals; it contains all one-sided nil ideals; etc. If  is an ideal of
is an ideal of 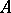 , then
, then 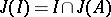 . If
. If  is the ring of all matrices of order
is the ring of all matrices of order  over
over 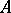 , then
, then
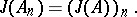 |
If the following  -composition is introduced on the associative ring
-composition is introduced on the associative ring  :
:
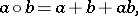 |
then the radical 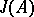 in the semi-group
in the semi-group 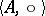 will be a subgroup with respect to the composition
will be a subgroup with respect to the composition  .
.
There are no non-zero irreducible finitely-generated modules over a quasi-regular associative ring (i.e. an associative ring coinciding with its own Jacobson radical), but there exist simple associative quasi-regular rings. The Jacobson radical of the associative ring 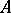 is zero if and only if
is zero if and only if 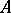 is a subdirect sum of primitive rings (cf. Primitive ring).
is a subdirect sum of primitive rings (cf. Primitive ring).
References
| [1] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) |
Comments
The Jacobson radical is the intersection of the right primitive ideals. It is also the intersection of the left primitive ideals. This is perhaps the most frequently occurring definition. Modular ideals are also called regular ideals. If  has a unit element, then all ideals are regular, so that in this case the Jacobson radical
has a unit element, then all ideals are regular, so that in this case the Jacobson radical  is the intersection of all right maximal ideals and also the intersection of all left maximal ideals. Nakayama's lemma says that if
is the intersection of all right maximal ideals and also the intersection of all left maximal ideals. Nakayama's lemma says that if  is a finitely-generated non-zero right
is a finitely-generated non-zero right 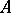 -module, then
-module, then  .
.
References
| [a1] | J.C. McConnell, J.C. Robson, "Noncommutative Noetherian rings" , Wiley (1987) |
| [a2] | I.N. Herstein, "Noncommutative rings" , Math. Assoc. Amer. (1968) |
Jacobson radical. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jacobson_radical&oldid=18564