Isogonal
Literally "same angle" . There are several concepts in mathematics involving isogonality.
Isogonal trajectory.
A trajectory that meets a given family of curves at a constant angle. See Isogonal trajectory.
Isogonal mapping.
A (differentiable) mapping that preserves angles. For instance, the stereographic projection of cartography has this property [a2]. See also Conformal mapping; Anti-conformal mapping.
Isogonal circles.
A circle is said to be isogonal with respect to two other circles if it makes the same angle with these two, [a1].
Isogonal line.
Given a triangle 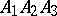 and a line
and a line 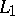 from one of the vertices, say from
from one of the vertices, say from 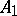 , to the opposite side. The corresponding isogonal line
, to the opposite side. The corresponding isogonal line 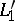 is obtained by reflecting
is obtained by reflecting 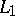 with respect to the bisectrix in
with respect to the bisectrix in 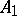 .
.
If the lines 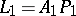 ,
,  and
and 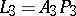 are concurrent (i.e. pass through a single point
are concurrent (i.e. pass through a single point 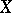 , i.e. are Cevian lines), then so are the isogonal lines
, i.e. are Cevian lines), then so are the isogonal lines 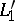 ,
, 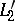 ,
, 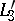 . This follows fairly directly from the Ceva theorem. The point
. This follows fairly directly from the Ceva theorem. The point 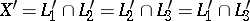 is called the isogonal conjugate point. If the barycentric coordinates of
is called the isogonal conjugate point. If the barycentric coordinates of 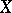 (often called trilinear coordinates in this setting) are
(often called trilinear coordinates in this setting) are 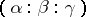 , then those of
, then those of 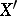 are
are 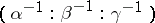

Figure: i130080a
Another notion in rather the same spirit is that of the isotomic line to 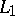 , which is the line
, which is the line 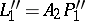 such that
such that 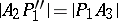 . Again it is true that if
. Again it is true that if 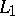 ,
, 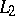 ,
, 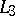 are concurrent, then so are
are concurrent, then so are 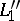 ,
, 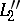 ,
, 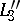 . This follows directly from the Ceva theorem.
. This follows directly from the Ceva theorem.

Figure: i130080b
The point 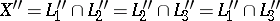 is called the isotomic conjugate point. The barycentric coordinates of
is called the isotomic conjugate point. The barycentric coordinates of 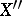 are
are 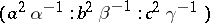 , where
, where  ,
, 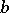 ,
,  are the lengths of the sides of the triangle. The Gergonne point is the isotomic conjugate of the Nagel point.
are the lengths of the sides of the triangle. The Gergonne point is the isotomic conjugate of the Nagel point.
The involutions 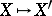 and
and  , i.e. isogonal conjugation and isotomic conjugation, are better regarded as involutions of the projective plane
, i.e. isogonal conjugation and isotomic conjugation, are better regarded as involutions of the projective plane 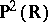 , [a4].
, [a4].
References
| [a1] | M. Berger, "Geometry" , I , Springer (1987) pp. 327 |
| [a2] | D. Hilbert, S. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) pp. 249 |
| [a3] | R.A. Johnson, "Modern geometry" , Houghton–Mifflin (1929) |
| [a4] | R.H. Eddy, J.B. Wilker, "Plane mappings of isogonal-isotomic type" Soochow J. Math. , 18 : 2 (1992) pp. 135–158 |
| [a5] | N. Altshiller–Court, "College geometry" , Barnes & Noble (1952) |
| [a6] | H.S.M. Coxeter, "The real projective plane" , Springer (1993) pp. 197–199 (Edition: Third) |
| [a7] | F. Bachmann, "Aufbau der Geometrie aus dem Spiegelungsbegriff" , Springer (1973) (Edition: Second) |
Isogonal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isogonal&oldid=12429