Invariant subspace of a representation
From Encyclopedia of Mathematics
 of a group (algebra, ring, semi-group)
of a group (algebra, ring, semi-group)  in a vector space (or topological vector space)
in a vector space (or topological vector space) 
A vector (respectively, a closed vector) subspace  such that for any
such that for any  and any
and any  one has
one has  . If
. If  is a projection operator from
is a projection operator from  onto
onto  , then
, then  is an invariant subspace of
is an invariant subspace of 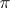 if and only if
if and only if  for all
for all 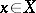 . The subspace
. The subspace  in
in  is invariant for any representation in
is invariant for any representation in  ; it is called the trivial invariant subspace; the remaining invariant subspaces (if there are any) are called non-trivial. See also Contraction of a representation; Completely-reducible set; Irreducible representation.
; it is called the trivial invariant subspace; the remaining invariant subspaces (if there are any) are called non-trivial. See also Contraction of a representation; Completely-reducible set; Irreducible representation.
How to Cite This Entry:
Invariant subspace of a representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Invariant_subspace_of_a_representation&oldid=12674
Invariant subspace of a representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Invariant_subspace_of_a_representation&oldid=12674
This article was adapted from an original article by A.I. Shtern (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article