Contraction of a representation

onto an invariant subspace

The contraction of a representation of a group onto a subgroup (of an algebra onto a subalgebra ) is the representation of the group (algebra) defined by the formula for all . A contraction of a representation 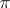is also called a restriction (or reduction) of the representation 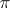onto an invariant subspace or onto a subgroup or subalgebra. If 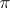is a continuous representation, then a contraction of 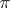is also continuous.

Comments

More usually one speaks of restriction of a representation and reduction of a representation. More precisely, if is a representation of a group, algebra and 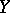is a subgroup, subalgebra 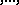then 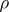can be restricted to 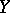. Secondly, if is an invariant subspace of , then induces a representation of (and ) in 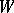yielding a subrepresentation of the given representation; this is sometimes called reduction of a representation to an invariant subspace. The phrase contraction of a representation refers more often to the following situation. Consider a representation 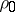over a ring of an algebra (or group) in an -module , . 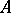Suppose that there is a representation of over , 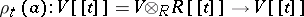such that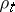 (i.e. 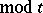for all ). Here 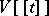denotes the module of power series in 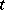with coefficients in . Then the representation is said to be a contraction of and is called a deformation of 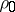. Intuitively is an (infinitesimal) family of representations parametrized by 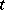. 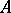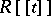More generally one also considers the situation where the algebra is also deformed at the same time, so that one has an algebra over such that 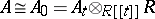and a representation of over . Cf. also Deformation.