Integral geometry
The theory of invariant measures (with respect to continuous groups of transformations of a space onto itself) on sets consisting of submanifolds of the space (for example, lines, planes, geodesics, convex surfaces, etc.; in other words, manifolds preserving their type under the transformations in question). Integral geometry has been constructed for various spaces, primarily Euclidean, projective and homogeneous spaces.
Integral geometry is concerned with the introduction of invariant measures (cf. Invariant measure), their relationships and their geometric applications. It arose in connection with refinements of statements of problems in geometric probabilities.
In order to introduce an invariant measure one tries to begin with a function depending on the coordinates of the space under consideration whose integral over some region of the space is not changed under any continuous coordinate transformation belonging to a specified Lie group. This requires finding an integral invariant of the Lie group. The latter can be found as a solution to the system of partial differential equations
$$ \tag{1 } \sum _ { i= } 1 ^ { n } \frac \partial {\partial x _ {i} } [ \xi _ {h} ^ {i} ( x) F ( x) ] = 0 ,\ \ h = - 1 \dots r , $$
where $ F ( x) $ is the required integral invariant, $ x $ is a point of the space (having dimension $ n $), $ \xi _ {h} ^ {i} $ are the coefficients of the infinitesimal transformation of the group, and $ r $ is the number of parameters of the transformation. Of great significance in integral geometry are measurable Lie groups, that is, groups that admit one and only one invariant (up to a constant factor). In particular, simple transitive groups are of this type.
The following problem in integral geometry consists of determining a measure on a set of manifolds that preserve their type under some group of continuous transformations. The measure is given by the integral
$$ \tag{2 } \int\limits _ {A _ \alpha } | F ( \alpha ^ {1} \dots \alpha ^ {q} ) | \ d \alpha ^ {1} \wedge \dots \wedge d \alpha ^ {q} , $$
where $ A _ \alpha $ is a set of points in the parameter space of the Lie group and $ F $ is an integral invariant of the group, defined by equation (1), or the density measure. The integral in (2) is also called an elementary measure of the set of manifolds. A specific choice of this measure sets up a complete correspondence with the fundamental problem in the study of geometric probabilities. In fact, the geometric probability of a set of manifolds having a property $ A _ {1} $ is the fraction of this set, regarded as a subset of the set of manifolds having a more general property $ A $. The problem reduces to establishing the measures of a set of manifolds with property $ A $ and of the subset with property $ A _ {1} $, and taking the ratio of them, the latter being the geometric probability.
In the case of a homogeneous multi-dimensional space, the measure of a set of manifolds (for example, points, straight lines, hyperplanes, pairs of hyperplanes, hyperspheres, second-order hypersurfaces) is uniquely defined (up to a constant factor) by the integral
$$ \tag{3 } \int\limits _ { X } d H = [ \omega _ {1} \dots \omega _ {h} ] , $$
where $ \{ \omega _ {i} \} _ {i=} 1 ^ {h} $ are the relative components of a given transitive Lie group $ G _ {2} $. Linear combinations with constant coefficients of these relative components are the left-hand sides of a system of Pfaffian equations corresponding to the set of manifolds under consideration. The measure (3) is called the kinematic measure in the homogeneous space with a given group of transformations defined on it. It is the generalization of the so-called Poincaré kinematic measure. (In what follows, all measures are given up to a constant factor.)
In integral geometry on the Euclidean plane $ E ^ {2} $ one usually considers only one type of continuous transformation, namely, the group of motions (without reflections). For a set of points, the integral invariant is the unit, for a set of lines it is again the unit if one selects for the parameters of the lines the parameters $ p $ and $ \phi $ of its normal equation. The length of an arbitrary curve is equal to $ \int n d p d \phi / 2 $, where $ n $ is the number of intersections of a straight line with the curve and the integration is carried out over the set of straight lines intersecting the curve. The measure of a set of straight lines intersecting two convex figures (ovals) is equal to the difference of the lengths of the crossed common tangent lines of the oval and the outer common tangent lines (see Fig. a). Outer common tangent lines Crossed common tangent lines
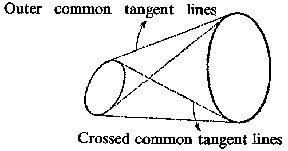
Figure: i051470a
The measure of the set of straight lines dividing two ovals is equal to the length of the crossed common tangent lines minus the sum of the lengths of the contours of the ovals. The measure of a set of pairs of points is determined as
$$ \int\limits | t _ {2} - t _ {1} | d p \wedge d \phi \wedge d t _ {1} \wedge d t _ {2} , $$
where $ p $, $ \phi $ are the parameters of the normal equation of the straight line passing through the points and $ t _ {1} $ and $ t _ {2} $ are the distances along this straight line from the points to the point on the line having minimal distance from the origin (see Fig. b).
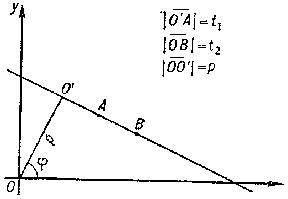
Figure: i051470b
The measure of a set of pairs of straight lines is equal to
$$ \int\limits | \sin ( \alpha _ {1} - \alpha _ {2} ) | \ d x \wedge d y \wedge d \alpha _ {1} \wedge d \alpha _ {2} , $$
where $ x $ and $ y $ are the coordinates of the point of intersection of the pair of straight lines and $ \alpha _ {1} $ and $ \alpha _ {2} $ are the angles that these lines form with one of the coordinates axes (see Fig. c.).
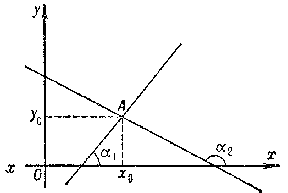
Figure: i051470c
The measure of the set of pairs of lines intersecting an oval is equal to half the square of the length of the curve bounding the oval minus the area of the oval multiplied by $ \pi $( Crofton's formula). An application of the kinematic measure to the set of congruent ovals intersecting a given oval enables one to obtain one of the isoperimetric inequalities, namely, the classical Bonnesen inequality. If
$$ I _ {n} = \int\limits _ { G } \sigma ^ {n} d p \ d \phi ,\ J _ {n} = \ \int\limits _ { H } r ^ {n} | t _ {2} - t _ {1} | d p \wedge d \phi \wedge d t _ {1} \wedge d t _ {2} , $$
where $ \sigma $ is the length of the Jordan oval $ H $, $ G $ is the set of straight lines intersecting the oval and $ r $ is the distance between two points in the interior of the oval, then
$$ J _ {n} = \ \frac{2 I _ {n+} 3 }{( n + 2 ) ( n + 3 ) } , $$
which enables one to determine the mean distance between two points inside the oval in a simple way. The kinematic measure of a set of figures is the measure of the set of figures congruent to the given one. It is equal to
$$ \int\limits _ { X } d x \wedge d y \wedge d \phi , $$
where $ X $ is the set of points of the figure, $ x , y $ are the coordinates of a fixed point of it and $ \phi $ is an angle defining the rotation of the figure. The kinematic measure can be regarded as the measure of a set of moving coordinate frames. If the fixed coordinate frame is made to move, while the moving frame is fixed, then for the same set of transformations the kinematic measure remains unaltered (symmetry of the kinematic measure). If another moving system is associated with each element of the set of congruent figures, then the kinematic measure is also preserved. The measure of the set of congruent finite arcs of an arbitrary curve intersecting a given arc of some curve is equal to four times the derivative of the length of the arcs (Poincaré's formula). The number of segments of given length $ l $ on a straight line intersecting an oval is equal to $ 2 \pi F _ {0} + 2 l L _ {0} $, where $ F _ {0} $ and $ L _ {0} $ are the area of the oval and the length of the curve bounding it. If the oval is replaced by a non-closed curve, then $ F _ {0} = 0 $ and the number of intersections is equal to $ 2 l L _ {0} $. The measure of the set of ovals intersecting a given oval is equal to $ 2 \pi ( F _ {0} + F ) + L _ {0} L $, where $ F _ {0} $ and $ F $ are the corresponding areas and $ L _ {0} $ and $ L $ the lengths of the curves bounding the ovals.
Integral geometry in Euclidean space $ E ^ {3} $ is constructed in a similar way as integral geometry in $ E ^ {2} $. For sets of points, the integral invariant is again equal to the unit. If a set of straight lines is given by the set of their equations in two projective planes,
$$ x = k z + a ,\ \ y = h z + b , $$
then the integral invariant for the set of parallel translations and rotations around axes is equal to $ ( k ^ {2} + h ^ {2} + 1 ) ^ {-} 2 $. In particular, the measure of the sets of straight lines intersecting a convex closed surface (the surface of an ovaloid) is equal to half the surface area of the ovaloid.
By introducing the measure of a set of pairs of points by analogy with $ E ^ {2} $, one is able to calculate the average value of the 4th power of the lengths of the chords of the ovaloid, which is equal to $ 12 V / \pi S $, where $ V $ and $ S $ are its volume and surface area. For pairs of intersecting straight lines defined by their equations in two projective planes:
$$ x = k _ {1} z + a - k _ {1} c ; \ \ y = h _ {1} z + b - h _ {1} c $$
and
$$ x = k _ {2} z + a - k _ {2} c ; \ \ y = h _ {2} z + b - h _ {2} c , $$
where $ a $, $ b $ and $ c $ are the coordinates of the points of intersection of the straight lines, it is equal to
$$ [ ( k _ {1} ^ {2} + h _ {1} ^ {2} + 1 ) ( k _ {2} ^ {2} + h _ {2} ^ {2} + 1 ) ] ^ {-} 3/2 . $$
The measures of the set of intersections of two given moving ovaloids are related in the same way as their volumes. For a plane, given by the equation in intercepts, the integral invariant is equal to
$$ ( a ^ {-} 2 + b ^ {-} 2 + c ^ {-} 2 ) ^ {-} 2 , $$
where $ a , b , c $ are the lengths of the intercepts. The measure of the set of planes intersecting a surface of area $ S $ is equal to $ \pi ^ {2} S / 2 $, while the average value of the lengths of the curves along which the ovaloid is intersected by the set of planes is equal to $ \pi S ^ {2} / 2 \overline{H}\; $, where $ \overline{H}\; $ is the total mean curvature.
The integral invariant for a pair of planes is equal to the product of the integral invariants of the sets of planes. The kinematic measure in $ E ^ {3} $ is equal to the product of the measure of the set of distinct oriented planes and the elementary kinematic measure in the orienting plane. The integral invariant for the rotation of a spatial figure having one fixed point is equal to
$$ 1 + l _ {1} ^ {2} + l _ {2} ^ {2} + l _ {3} ^ {2} , $$
where $ l _ {i} = \alpha _ {i} \mathop{\rm tan} ( \phi / 2 ) $, $ i = 1 , 2 , 3 $, $ \alpha _ {i} $ are the direction cosines of the axis of rotation and $ \phi $ is the angle of rotation around this axis. The measure of a set of bodies having a common point and differing by a rotation in space is equal to $ \pi ^ {2} $.
Integral geometry on a surface is constructed by the introduction of a measure on the set of geodesics as the integral of an exterior differential form on the surface over the whole set. Thus, the exterior differential form is the density of the set of geodesics, since it is invariant with respect to the choice of the system of curvilinear coordinates on the surface and with respect to the choice of the parameter defining the position of points on a geodesic. In geodesic polar coordinates the density has the form
$$ d G = \ \left ( \frac{\partial \sqrt {g ( \rho , \theta ) } }{\partial \rho } \right ) [ d \theta d \rho ] . $$
In particular, for the sphere $ d G = \cos \rho [ d \theta d \rho ] $, while for a pseudo-sphere, $ d G = \cosh \rho [ d \theta d \rho ] $. For the set of geodesics intersecting a smooth or piecewise-smooth curve, the density is equal to $ d G = | \sin \phi | [ d \phi d s ] $, where $ \phi $ is the angle of intersection and $ s $ is the arc length of the curve. The density of the kinematic measure (the kinematic density) is equal to $ d K = [ d P d V ] $, where $ d P $ is the area element of the surface and $ V $ is the angle between the geodesic and the polar radius. Many of the results of integral geometry on $ E ^ {2} $ generalize to the case of a homogeneous surface. The density of the measure of a set is the kinematic density, which enables one to obtain a generalization of Poincaré's formula for $ E ^ {2} $. The measure of the set of pairs of geodesics and pairs of points is constructed in the same way as for $ E ^ {2} $.
On the basis of the so-called polymetric geometry of P.K. Rashevskii (see [4]), the results of integral geometry on an arbitrary homogeneous surface can be generalized to a broader class of surfaces. The generalizations are carried out by the use of Rashevskii's bimetric system. To begin with, the measure is introduced on a two-parameter set of curves of the plane by two methods. Then, all the conclusions valid for the case of the plane (considered as a set of line elements) are generalized to the case of lines of constant geodesic curvature on an arbitrary surface.
Integral geometry on the projective plane $ P ^ {2} $. An integral invariant for the full group of projective transformations on $ P ^ {2} $,
$$ \tag{4 } x ^ \prime = \ \frac{a _ {1} x + b _ {1} y + c _ {1} }{a _ {3} x + b _ {3} y + 1 } ,\ \ y ^ \prime = \ \frac{a _ {2} x + b _ {2} y + c _ {2} }{a _ {3} x + b _ {3} y + 1 } , $$
exists only for triples of points and is equal to the cube of the reciprocal of the area of the triangle having these points as vertices. For pairs of points and the group of affine unimodular transformations
$$ \tag{5 } \left . \begin{array}{c} x ^ \prime = a _ {1} x + b _ {1} y + c _ {1} , \\ y ^ \prime = a _ {2} x + b _ {2} y + c _ {2} , \\ a _ {1} b _ {2} - a _ {2} b _ {1} = 1 , \\ \end{array} \right \} $$
the integral invariant is equal to the unit, while for the group of affine transformations the integral invariant of the set of pairs of points is equal to $ ( x _ {1} y _ {2} - x _ {2} y _ {1} ) ^ {-} 2 $, where $ x _ {1} , y _ {1} $ and $ x _ {2} , y _ {2} $ are the coordinates of the points.
The set of straight lines of the projective plane is non-measurable, but for point-line pairs and the full group of projective transformations (4) the integral invariant is equal to $ ( x _ {0} \alpha + y _ {0} \beta + 1 ) ^ {-} 3 $, where $ x _ {0} $, $ y _ {0} $ are the coordinates of the point and the straight line is given by the equation $ \alpha x + \beta y + 1 = 0 $. The set of parallelograms given by the equations
$$ \left . \begin{array}{c} \alpha _ {i} x + \beta _ {i} y + 1 = 0 \\ \gamma _ {i} ( \alpha _ {i} x + \beta _ {i} y ) + 1 = 0 \\ \end{array} \right \} ,\ \ i = 1 , 2 , $$
where $ \alpha _ {1} \beta _ {2} - \alpha _ {2} \beta _ {1} \neq 0 $, has density measure
$$ [ ( \gamma _ {1} - 1 ) ^ {2} ( \alpha _ {2} \beta _ {2} - \alpha _ {2} \beta _ {1} ) ^ {2} ] ^ {-} 1 $$
for the group of affine transformations
$$ \tag{6 } \left . \begin{array}{c} x ^ \prime = a _ {1} x + b _ {1} y + c _ {1} , \\ y ^ \prime = a _ {2} x + b _ {2} y + c _ {2} , \\ a _ {1} b _ {2} - a _ {2} b _ {1} \neq 0 \\ \end{array} \right \} . $$
For the set of circles on $ P ^ {2} $ given by the equation
$$ x ^ {2} + y ^ {2} - 2 \alpha x - 2 \beta y + \gamma = 0 , $$
the maximal group of transformations is the group of similarity transformations
$$ x = a x ^ \prime + b y ^ \prime + c ,\ \ y = b x ^ \prime + a y ^ \prime + d . $$
Their density measure is given by $ ( \gamma - \alpha ^ {2} - \beta ^ {2} ) ^ {-} 2 $. On this basis, the measures of sets of circles (whose centres are in some domain) intersecting a given curve can be calculated. The measure of a set of circles on $ P ^ {2} $ is equal to the kinematic measure for the transformations generated by translations and homotheties.
The set of conic sections (invariant $ \Delta \neq 0 $) has as its maximal group of invariants the projective group:
$$ x = \ \frac{\alpha _ {11} x ^ \prime + \alpha _ {12} y ^ \prime + \alpha _ {13} }{\alpha _ {31} x ^ \prime + \alpha _ {32} y ^ \prime + 1 } ,\ \ y = \ \frac{\alpha _ {21} x ^ \prime + \alpha _ {22} y ^ \prime + \alpha _ {23} }{\alpha _ {31} x ^ \prime + \alpha _ {32} y ^ \prime + 1 } , $$
where $ \mathop{\rm det} | \alpha _ {ij} | \neq 0 $, $ i , j = 1 , 2 , 3 $. Its density measure is equal to $ \Delta ^ {-} 2 $. For the set of hyperbolas, the maximal group of invariants is the affine group (6). Their density measure is equal to $ a ^ {-} 1 \Delta ^ {-} 2 \sqrt {b ^ {2} - a c } $, where $ a $, $ b $, $ c $ are the coefficients of the general equation of the hyperbola. Similarly, the maximal group of invariants of ellipses is measurable, but for parabolas it is non-measurable. For parabolas, only subgroups of it are measurable, such as the groups of unimodular affine and centro-affine transformations. The elementary kinematic measure of the group of projective transformations (4) is equal to $ \Delta ^ {-} 3 $, where $ \Delta $ is the determinant of the transformation.
The set of lines of the centro-affine plane is measurable. Their density measure is equal to $ p ^ {-} 3 $, where $ p $ is the free term of the normal equation of the line. The kinematic measure of the group of transformations (5) of the non-centro-affine plane is equal to $ a ^ {-} 1 $. If $ \Delta = \Delta ( \phi ) $ is the width of an oval, then $ \Delta ^ {-} 2 $ is its density measure for the affine unimodular transformations.
Integral geometry in the projective space $ P ^ {3} $. The group of motions in projective space $ P ^ {3} $ with a rectangular Cartesian coordinate system is measurable only for the set of quadruples of points. The density measure in this case is equal to $ \Delta ^ {-} 4 $, where $ \Delta $ is the volume of the tetrahedron whose vertices are the points. For pairs and triples of points, only the group of affine unimodular transformations is measurable. Its density measure is equal to the unit. For triples of points, the group of centro-affine transformations is also measurable (provided that the points do not lie on the same line). The set of straight lines in $ P ^ {3} $ has as its maximal group of invariance the full group of motions, but it is non-measurable for them (only a certain subgroup of it is measurable). The full group of transformations for pairs of straight lines is measurable. The set of planes does not admit a measure with respect to the full group of transformations in $ P ^ {3} $; for the set of planes, only its subgroup of orthogonal transformations is measurable. Pairs of planes admit a measure for the group of centro-affine unimodular transformations. Parallelopipeds admit a measure for the subgroup of affine transformations, the set of pairs of planes-points admits a measure for the full group of transformations in $ P ^ {3} $. The set of spheres in $ P ^ {3} $ admits a measure for the group of similarity transformations, the density being equal to $ R ^ {-} 4 $, where $ R $ is the radius of the sphere. The set of second-order surfaces admits a measure for the full group of transformations in $ P ^ {3} $, the density being $ \Delta ^ {-} 5 $, where $ \Delta $ is the invariant of the surface. The set of circles in $ P ^ {3} $ admits a measure for the group of similarity transformations, the density being equal to $ R ^ {-} 4 $, where $ R $ is the radius of the circle. The kinematic measure in $ P ^ {3} $ of the full group of transformations is equal to $ \Delta ^ {-} 4 $, where $ \Delta $ is its determinant. The density measure of a set of points in three-dimensional centro-affine unimodular space is equal to the unit. The set of planes in space is also measurable, with density $ p ^ {-} 4 $, where $ p $ is the parameter of the normal equation of the plane.
Integral geometry on a surface $ V ^ {2} $ of constant curvature. The family of curves in $ V ^ {2} $ with constant positive curvature has $ G _ {3} ^ {+} ( x) $ as maximal group of invariance. Families of special type (three-, two- and one-parameter) admit a density measure for the maximal group of invariance (infinitesimal transformations of the group $ G _ {3} ^ {+} ( x) $), and for $ G _ {1} ( x) $ in the one-parameter case.
The same holds for $ V ^ {2} $ with negative constant curvature. Three-parameter curves of special type admit a density measure for $ G _ {3} ^ {-} ( x) $ as maximal group of invariance; it is equal to the unit. Measures also exists for groups in the case of special type of two- and one-parameter families. In both cases, the condition that the family of curves $ F _ {q} ( x) $ have a measure for $ G _ {2} ( x) $ as maximal group of invariance is that the adjoint group $ H _ {2} ( \alpha ) $ be spatially transitive (measurable).
Generalizations of integral geometry. The above account relates to the traditional understanding of the content of integral geometry as a theory of invariant measures on sets of geometric objects in various spaces, mainly in homogeneous spaces. In the sense of integral geometry as a theory of transformation of functions given on a set of certain geometric objects in some space into functions defined on a set of other geometric objects of the same space, the problem converse to integrating some function of points of the space along some geometric objects of the same space is posed as the fundamental problem. For example, if an integral transform of a function $ f $ in $ n $- dimensional affine space (a Radon transform) is introduced as its integral over hypersurfaces, then the converse problem is to recover $ f $ in terms of its integral over the hypersurfaces, that is, the problem of finding the inverse Radon transform. Similarly, problems have been posed and solved concerning recovering functions on ruled second-order surfaces in four-dimensional complex space for which the integrals over the straight lines forming this surface are known, and also the question of recovering a function in terms of its integral taken over horospheres in a real or imaginary Lobachevskii space.
References
| [1] | W. Blaschke, "Vorlesungen über Integralgeometrie" , Deutsch. Verlag Wissenschaft. (1955) |
| [2] | L.A. Santaló, "Introduction to integral geometry" , Hermann (1953) |
| [3] | I.M. Gel'fand, M.I. Graev, N.Ya. Vilenkin, "Generalized functions" , 5. Integral geometry and representation theory , Acad. Press (1965) (Translated from Russian) |
| [4] | P.K. Rashevskii, "Polymetric geometry" , Proc. Sem. Vektor. Tenzor. Anal. , 5 , Moscow-Leningrad (1941) pp. 21–147 (In Russian) |
| [5] | M.I. Stoka, "Géométrie intégrale" , Gauthier-Villars (1968) |
| [6] | G.I. Drinfel'd, "Integral geometry" Progress in Math. , 12 (1972) pp. 173–214 Itogi Nauk. Algebra. Topol. Geom. 1968 (1970) pp. 157–191 |
Comments
Reference [a1] gives a fairly complete survey of classical integral geometry up to 1976. Part of the more recent development was essentially influenced by an important paper of H. Federer [a2], who extended the classical kinematic and Crofton intersection formulas to curvature measures and sets of positive reach. Some of the later integral-geometric results involving curvature measures are described in the survey articles [a3], [a4]. Integral geometry plays an essential role in the recent development of stochastic geometry, as in the work of R.E. Miles, e.g. [a5], G. Matheron [a6], and others. The use of kinematic formulas for curvature measures in stochastic geometry can be seen in the articles [a7], [a8].
Another new branch of integral geometry is the combinatorial integral geometry developed by R.V. Ambartzumian [a9]. This theory, in which combinatorial relations between measures of certain sets of geometric objects play a central role, and invariance properties are not necessarily assumed, has also applications to stochastic geometry and interesting connections to Hilbert's fourth problem.
An impression of the scope of the "generalizations of integral geometry" as it is called in the main article above, can be obtained from the contributions of the conference proceedings [a10], and from [a11].
References
| [a1] | L.A. Santaló, "Integral geometry and geometric probability" , Addison-Wesley (1976) |
| [a2] | H. Federer, "Curvature measures" Trans. Amer. Math. Soc. , 93 (1959) pp. 418–491 |
| [a3] | W. Weil, "Kinematic integral formulas for convex bodies" J. Tölke (ed.) J.M. Wills (ed.) , Contributions to geometry , Birkhäuser (1979) pp. 60–76 |
| [a4] | R. Schneider, J.A. Wieacker, "Random touching of convex bodies" R. Ambartzumian (ed.) W. Weil (ed.) , Stochastic Geometry, Geometric Statistics, Stereology , Teubner (1984) pp. 154–169 |
| [a5] | R.E. Miles, "Some new integral geometric formulae, with stochastic applications" J. Appl. Prob. , 16 (1979) pp. 592–606 |
| [a6] | G. Matheron, "Random sets and integral geometry" , Wiley (1975) |
| [a7] | W. Weil, "Stereology: A survey for geometers" P.M. Gruber (ed.) J.M. Wills (ed.) , Convexity and its applications , Birkhäuser (1983) pp. 360–412 |
| [a8] | W. Weil, "Point processes of cylinders, particles and flats" Acta. Applic. Math. , 9 (1987) pp. 103–136 |
| [a9] | R.V. [R.V. Ambartsumyan] Ambartzumian, "Combinatorial integral geometry" , Wiley (1982) |
| [a10] | R.L. Bryant (ed.) V. Guillemin (ed.) S. Helgason (ed.) R.O. Wells jr. (ed.) , Integral geometry , Amer. Math. Soc. (1987) |
| [a11] | R.V. (ed.) Ambartzumian, "Stochastic and integral geometry" Acta. Applic. Math. , 9 : 1–2 (1987) |
Integral geometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_geometry&oldid=47374