Imbedding of rings
A monomorphism of a ring into another ring; a ring 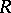 is imbeddable in a ring
is imbeddable in a ring 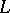 if
if 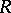 is isomorphic to a subring of
is isomorphic to a subring of 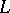 . The conditions for imbedding of an associative ring in an (associative) skew-field and of an arbitrary ring into a division ring have been studied in great detail. These studies were initiated by A.I. Mal'tsev [1], who constructed an example of an associative ring without zero divisors and not imbeddable in a skew-field. The following Mal'tsev problem remained an open question for a long time: Is any associative ring without zero divisors and for which the semi-group of non-zero elements is imbeddable in a group, imbeddable in a skew-field? This problem was negatively answered in 1966 (cf. [2]). A square matrix
. The conditions for imbedding of an associative ring in an (associative) skew-field and of an arbitrary ring into a division ring have been studied in great detail. These studies were initiated by A.I. Mal'tsev [1], who constructed an example of an associative ring without zero divisors and not imbeddable in a skew-field. The following Mal'tsev problem remained an open question for a long time: Is any associative ring without zero divisors and for which the semi-group of non-zero elements is imbeddable in a group, imbeddable in a skew-field? This problem was negatively answered in 1966 (cf. [2]). A square matrix 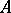 of order
of order 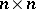 over an associative ring
over an associative ring 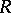 is said to be non-full if it can be represented in the form
is said to be non-full if it can be represented in the form 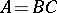 where
where 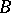 ,
, 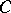 are matrices of orders
are matrices of orders 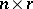 and
and 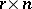 , respectively, and
, respectively, and 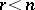 . Let
. Let
 |
be square matrices of order 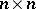 over
over 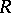 in which all columns (except, possibly, the first column) are identical. Then the matrix
in which all columns (except, possibly, the first column) are identical. Then the matrix
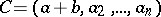 |
is said to be the determinant sum of 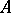 and
and 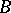 with respect to the first column. The determinant sum of square matrices of the same order with respect to an arbitrary column (row) is defined in a similar manner. An associative ring
with respect to the first column. The determinant sum of square matrices of the same order with respect to an arbitrary column (row) is defined in a similar manner. An associative ring 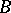 with a unit element is imbeddable in a skew-field if and only if it has no zero divisors and if no scalar matrix
with a unit element is imbeddable in a skew-field if and only if it has no zero divisors and if no scalar matrix 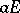 with a non-zero element
with a non-zero element  along the diagonal can be represented as the determinant sum of a finite number of non-full matrices [2]. The class of associative rings imbeddable in skew-fields is not finitely axiomatized (i.e. cannot be defined by a finite number of axioms) [3]. A number of sufficient conditions for imbedding of an associative ring in a skew-field are known; the following are the most important. Let
along the diagonal can be represented as the determinant sum of a finite number of non-full matrices [2]. The class of associative rings imbeddable in skew-fields is not finitely axiomatized (i.e. cannot be defined by a finite number of axioms) [3]. A number of sufficient conditions for imbedding of an associative ring in a skew-field are known; the following are the most important. Let 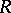 be an associative ring without zero divisors and for which the semi-group of non-zero elements satisfies Ore's condition (cf. Imbedding of semi-groups). Then
be an associative ring without zero divisors and for which the semi-group of non-zero elements satisfies Ore's condition (cf. Imbedding of semi-groups). Then 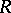 is imbeddable in a skew-field [4]. The group algebra of an ordered group is imbeddable in a skew-field (the Mal'tsev–Neumann theorem, cf. [4]). An arbitrary domain of free right (left) ideals (cf. Associative rings and algebras) is imbeddable in a skew-field [2].
is imbeddable in a skew-field [4]. The group algebra of an ordered group is imbeddable in a skew-field (the Mal'tsev–Neumann theorem, cf. [4]). An arbitrary domain of free right (left) ideals (cf. Associative rings and algebras) is imbeddable in a skew-field [2].
A ring 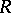 is imbeddable in a division ring if and only if it has no zero divisors. Let
is imbeddable in a division ring if and only if it has no zero divisors. Let 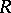 ,
, 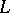 be rings, let
be rings, let 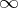 be a symbol,
be a symbol, 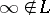 . A mapping
. A mapping 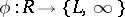 is said to be a
is said to be a 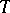 -homomorphism if: 1) the set
-homomorphism if: 1) the set 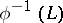 is a ring and the mapping
is a ring and the mapping 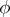 on this set is a ring homomorphism; 2) it follows from
on this set is a ring homomorphism; 2) it follows from 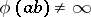 ,
, 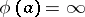 that
that 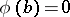 ; and 3) it follows from
; and 3) it follows from 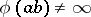 ,
, 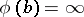 that
that 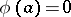 . A
. A 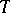 -homomorphism of a field is nothing but a specialization (of a point) of the field (cf. Specialization of a point). A division ring
-homomorphism of a field is nothing but a specialization (of a point) of the field (cf. Specialization of a point). A division ring 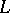 is a free
is a free 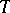 -extension of a ring
-extension of a ring 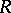 if
if 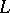 includes
includes 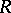 and is generated (as a division ring) by the ring
and is generated (as a division ring) by the ring 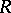 , while any
, while any 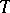 -homomorphism of the ring
-homomorphism of the ring 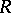 into some division ring
into some division ring 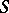 may be extended to a
may be extended to a 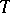 -homomorphism of
-homomorphism of 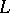 into
into 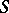 . Every ring without zero divisors has a free
. Every ring without zero divisors has a free 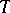 -extension [4].
-extension [4].
References
| [1] | A.I. [A.I. Mal'tsev] Malcev, "On the immersion of an algebraic ring into a field" Math. Ann. , 113 (1937) pp. 686–691 |
| [2] | P.M. Cohn, "Free rings and their relations" , Acad. Press (1971) |
| [3] | P.M. Cohn, "The class of rings embeddable in skew fields" Bull. London Math. Soc. , 6 (1974) pp. 147–148 |
| [4] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
| [5] | L.A. Bokut', "Embedding of rings" Russian Math. Surveys , 42 : 4 (1987) pp. 105–138 Uspekhi Mat. Nauk , 42 (1987) pp. 87–111 |
Comments
A 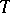 -homomorphism is also called a localization (cf. also Localization in a commutative algebra).
-homomorphism is also called a localization (cf. also Localization in a commutative algebra).
Another classical problem is imbedding of a ring 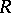 in a finite matrix ring over a commutative ring. A necessary condition is that it satisfies all universal polynomial identities
in a finite matrix ring over a commutative ring. A necessary condition is that it satisfies all universal polynomial identities 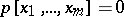 of the
of the 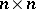 matrix ring over the integers. The condition is sufficient if
matrix ring over the integers. The condition is sufficient if  is prime or semi-prime, but fails in other cases (cf. [a1]).
is prime or semi-prime, but fails in other cases (cf. [a1]).
References
| [a1] | L.H. Rowen, "Polynomial identities in ring theory" , Acad. Press (1980) pp. Chapt. 7 |
Imbedding of rings. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Imbedding_of_rings&oldid=19119