Idempotents, semi-group of
idempotent semi-group
A semi-group each element of which is an idempotent. An idempotent semi-group is also called a band (this is consistent with the concept of a band of semi-groups: An idempotent semi-group is a band of one-element semi-groups). A commutative idempotent semi-group is called a semi-lattice; this term is consistent with its use in the theory of partially ordered sets: If a commutative idempotent semi-group 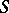 is considered with respect to its natural partial order, then
is considered with respect to its natural partial order, then 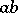 is the greatest lower bound of the elements
is the greatest lower bound of the elements 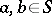 . Every semi-lattice is a subdirect product of two-element semi-lattices. A semi-group
. Every semi-lattice is a subdirect product of two-element semi-lattices. A semi-group 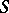 is said to be singular if
is said to be singular if 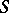 satisfies one of the identities
satisfies one of the identities 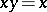 ,
, 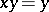 ; in the first case
; in the first case 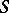 is said to be left-singular, or to be a semi-group of left zeros, in the second case it is called right-singular, or a semi-group of right zeros. A semi-group is said to be rectangular if it satisfies the identity
is said to be left-singular, or to be a semi-group of left zeros, in the second case it is called right-singular, or a semi-group of right zeros. A semi-group is said to be rectangular if it satisfies the identity 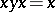 (this term is sometimes used in a wider sense, see [1]). The following conditions are equivalent for a semi-group
(this term is sometimes used in a wider sense, see [1]). The following conditions are equivalent for a semi-group 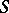 : 1)
: 1) 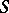 is rectangular; 2)
is rectangular; 2) 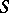 is an ideally-simple idempotent semi-group (see Simple semi-group); 3)
is an ideally-simple idempotent semi-group (see Simple semi-group); 3) 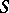 is a completely-simple semi-group of idempotents; and 4)
is a completely-simple semi-group of idempotents; and 4)  is isomorphic to a direct product
is isomorphic to a direct product 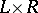 , where
, where 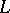 is a left-singular and
is a left-singular and 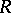 is a right-singular semi-group. Every idempotent semi-group is a Clifford semi-group and splits into a semi-lattice of rectangular semi-groups (see Band of semi-groups). This splitting is the starting point for the study of many properties of idempotent semi-groups. Every idempotent semi-group is locally finite.
is a right-singular semi-group. Every idempotent semi-group is a Clifford semi-group and splits into a semi-lattice of rectangular semi-groups (see Band of semi-groups). This splitting is the starting point for the study of many properties of idempotent semi-groups. Every idempotent semi-group is locally finite.
Idempotent semi-groups have been studied from various points of view, including that of the theory of varieties. The lattice of all subvarieties of the variety 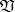 of all idempotent semi-groups has been described completely in [4]–[6]; it is countable and distributive, and every subvariety of
of all idempotent semi-groups has been described completely in [4]–[6]; it is countable and distributive, and every subvariety of 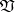 is defined by one identity. See the figure for the diagram of this lattice; also indicated in this figure are the identities giving in
is defined by one identity. See the figure for the diagram of this lattice; also indicated in this figure are the identities giving in 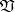 the varieties on some of the lower "floors" .
the varieties on some of the lower "floors" .

Figure: i050090a
References
| [1] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1–2 , Amer. Math. Soc. (1961–1967) |
| [2] | A.D. McLean, "Idempotent semigroups" Amer. Math. Monthly , 61 : 2 (1954) pp. 110–113 |
| [3] | N. Kimura, "The structure of idempotent semigroups" Pacific J. Math. , 8 (1958) pp. 257–275 |
| [4] | A.P. Biryukov, "Varieties of idempotent semigroups" Algebra and Logic , 9 : 3 (1970) pp. 153–164 Algebra i Logika , 9 : 3 (1970) pp. 255–273 |
| [5] | J. Gerhard, "The lattice of equational classes of idempotent semigroups" J. of Algebra , 15 : 2 (1970) pp. 195–224 |
| [6] | C. Fennemore, "All varieties of bands I, II" Math. Nachr. , 48 : 1–6 (1971) pp. 237–252; 253–262 |
Idempotents, semi-group of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Idempotents,_semi-group_of&oldid=16549