Difference between revisions of "Hyperbolic paraboloid"
(Importing text file) |
(TeX done and links) |
||
| Line 1: | Line 1: | ||
| − | + | {{TEX|done}} | |
| − | < | + | <span id="Fig1"> |
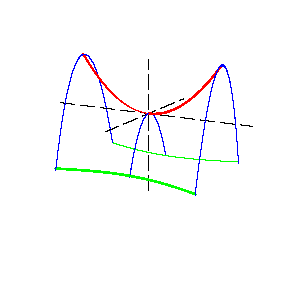
| + | [[File:Hyperbolic-paraboloid-1.gif| right| frame| Figure 1. A hyperbolic paraboloid]] | ||
| + | </span> | ||
| − | Sections of a hyperbolic paraboloid by planes parallel to the planes | + | A non-closed non-central [[surface of the second order]]. In a suitable coordinate system (see [[#Fig1|Figure 1]]) the equation of a hyperbolic paraboloid is |
| + | \begin{equation} | ||
| + | \frac{x^2}{p}-\frac{y^2}{q}=2z, \qquad\text{where}\;p,q>0. | ||
| + | \end{equation} | ||
| + | Sections of a hyperbolic paraboloid by planes parallel to the planes $xOz$ and $yOz$ are [[parabola]]s, while sections by planes parallel to the plane $xOy$ are [[hyperbola]]s (the section by the plane $xOy$ consists of two straight lines). The symmetry axis of a hyperbolic paraboloid is said to be its axis; the point of intersection of a hyperbolic paraboloid with the axis is known as the apex. If $p=q$, the hyperbolic paraboloid has two axes of symmetry. | ||
| − | + | A hyperbolic paraboloid is a [[ruled surface]]; the equations of the rectilinear generators passing through a given point $(x_0,y_0,z_0)$ have the form | |
| + | \begin{equation} | ||
| + | \begin{aligned} | ||
| + | \frac{x-x_0}{\sqrt{p}}=\frac{y-y_0}{\sqrt{q}}=\frac{z-z_0}{\frac{x_0}{\sqrt{p}}-\frac{y_0}{\sqrt{q}}}, \\ | ||
| + | \frac{x-x_0}{\sqrt{p}}=\frac{y-y_0}{-\sqrt{q}}=\frac{z-z_0}{\frac{x_0}{\sqrt{p}}-\frac{y_0}{\sqrt{q}}}. | ||
| + | \end{aligned} | ||
| + | \end{equation} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ====References==== | ||
| − | + | <table> | |
| − | + | <TR><TD valign="top">[1]</TD> <TD valign="top"> M. Berger, "Geometry" , '''1–2''' , Springer (1987) (Translated from French)</TD></TR> | |
| − | + | <TR><TD valign="top">[2]</TD> <TD valign="top"> D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German)</TD></TR> | |
| − | + | </table> | |
| − | |||
| − | <table><TR><TD valign="top">[ | ||
Latest revision as of 11:12, 25 May 2016
A non-closed non-central surface of the second order. In a suitable coordinate system (see Figure 1) the equation of a hyperbolic paraboloid is \begin{equation} \frac{x^2}{p}-\frac{y^2}{q}=2z, \qquad\text{where}\;p,q>0. \end{equation} Sections of a hyperbolic paraboloid by planes parallel to the planes $xOz$ and $yOz$ are parabolas, while sections by planes parallel to the plane $xOy$ are hyperbolas (the section by the plane $xOy$ consists of two straight lines). The symmetry axis of a hyperbolic paraboloid is said to be its axis; the point of intersection of a hyperbolic paraboloid with the axis is known as the apex. If $p=q$, the hyperbolic paraboloid has two axes of symmetry.
A hyperbolic paraboloid is a ruled surface; the equations of the rectilinear generators passing through a given point $(x_0,y_0,z_0)$ have the form \begin{equation} \begin{aligned} \frac{x-x_0}{\sqrt{p}}=\frac{y-y_0}{\sqrt{q}}=\frac{z-z_0}{\frac{x_0}{\sqrt{p}}-\frac{y_0}{\sqrt{q}}}, \\ \frac{x-x_0}{\sqrt{p}}=\frac{y-y_0}{-\sqrt{q}}=\frac{z-z_0}{\frac{x_0}{\sqrt{p}}-\frac{y_0}{\sqrt{q}}}. \end{aligned} \end{equation}
References
| [1] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
| [2] | D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German) |
Hyperbolic paraboloid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_paraboloid&oldid=38839