Homotopy group
A generalization of the fundamental group, proposed by W. Hurewicz [1] in the context of problems on the classification of continuous mappings. Homotopy groups are defined for any 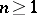 . For
. For 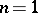 the homotopy group is identical with the fundamental group. The definition of homotopy groups is not constructive and for this reason their computation is a difficult task, general methods for which were developed only in the 1950s. Their importance is due to the fact that all problems in homotopy theory can be reduced (cf. Homotopy type), to a greater or lesser extent, to the computation of certain homotopy groups.
the homotopy group is identical with the fundamental group. The definition of homotopy groups is not constructive and for this reason their computation is a difficult task, general methods for which were developed only in the 1950s. Their importance is due to the fact that all problems in homotopy theory can be reduced (cf. Homotopy type), to a greater or lesser extent, to the computation of certain homotopy groups.
Let
 |
be the dimensional unit cube, let 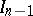 be its face
be its face  , and let
, and let 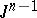 be the union of its remaining faces. For any pointed pair
be the union of its remaining faces. For any pointed pair 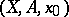 (cf. Pointed object) the symbol
(cf. Pointed object) the symbol 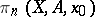 (or simply
(or simply 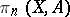 ) denotes the pointed set of all homotopy classes (cf. Homotopy) of mappings
) denotes the pointed set of all homotopy classes (cf. Homotopy) of mappings
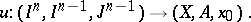 |
The distinguished (zero) element of this set is the constant mapping that maps the whole cube 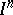 into
into 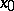 . Any continuous mapping
. Any continuous mapping
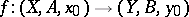 |
induces a morphism
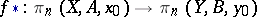 |
of pointed sets. For any 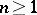 the sets
the sets 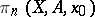 and the morphisms
and the morphisms 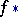 constitute a functor
constitute a functor  from the category of pointed pairs into the category of pointed sets. This functor is homotopy invariant, i.e.
from the category of pointed pairs into the category of pointed sets. This functor is homotopy invariant, i.e. 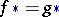 if
if 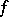 and
and 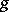 are homotopic (as mappings of pointed pairs). Furthermore, it is normalized in the sense that if
are homotopic (as mappings of pointed pairs). Furthermore, it is normalized in the sense that if 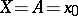 , then
, then 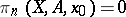 .
.
For 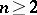 it is possible to introduce into the set
it is possible to introduce into the set 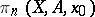 an operation of addition, with respect to which it becomes a group (if
an operation of addition, with respect to which it becomes a group (if 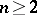 even an Abelian group). By definition, if
even an Abelian group). By definition, if 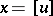 and
and  , then
, then 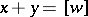 , where
, where 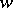 is the mapping
is the mapping
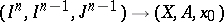 |
defined by the formula
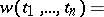 | (1) |
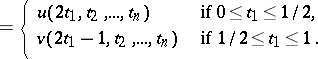 |
The resulting group 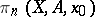 is said to be the
is said to be the  -th homotopy group (or the
-th homotopy group (or the  -dimensional homotopy group) of the pointed pair
-dimensional homotopy group) of the pointed pair  ; one also speaks of the homotopy group of the pair
; one also speaks of the homotopy group of the pair 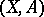 at
at 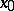 or of the homotopy group of the space
or of the homotopy group of the space 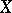 with respect to the subspace
with respect to the subspace 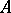 at
at 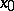 . The mappings
. The mappings 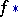 are homomorphisms of these groups. Thus, if
are homomorphisms of these groups. Thus, if 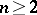 it may be assumed that the function
it may be assumed that the function 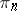 takes values in the category of groups (if
takes values in the category of groups (if 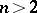 even in the category of Abelian groups).
even in the category of Abelian groups).
For 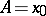 the group
the group 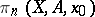 is denoted by
is denoted by 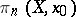 , or simply by
, or simply by 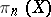 , and is called the absolute homotopy group of the pointed space
, and is called the absolute homotopy group of the pointed space 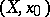 (or of the space
(or of the space 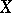 at
at 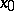 ). Its elements are the homotopy classes of mappings
). Its elements are the homotopy classes of mappings 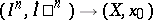 , where
, where 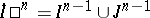 is the boundary of the cube
is the boundary of the cube 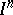 . For such mappings formula (1) is meaningful for
. For such mappings formula (1) is meaningful for 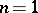 as well, and so
as well, and so  is a group. This group coincides with the classical fundamental group. The group operation in
is a group. This group coincides with the classical fundamental group. The group operation in 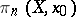 is usually called multiplication. This group is, generally speaking, non-Abelian, while the group
is usually called multiplication. This group is, generally speaking, non-Abelian, while the group 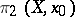 is Abelian. For any
is Abelian. For any 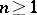 the groups
the groups  and the corresponding homomorphisms form a functor from the category of pointed spaces into the category of groups (if
and the corresponding homomorphisms form a functor from the category of pointed spaces into the category of groups (if 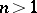 into the category of Abelian groups). This functor is the composition
into the category of Abelian groups). This functor is the composition 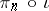 of the imbedding functor
of the imbedding functor 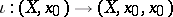 and the functor
and the functor 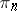 described above.
described above.
The functor 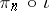 is extended to include the case
is extended to include the case 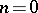 , where
, where 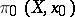 is the pointed set of path-components (cf. Path-connected space) of
is the pointed set of path-components (cf. Path-connected space) of 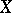 ; the zero of this set is the component containing
; the zero of this set is the component containing 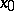 . The set
. The set 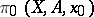 is not defined for
is not defined for 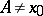 . In order to simplify the formulations, the sets
. In order to simplify the formulations, the sets 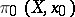 and
and 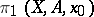 are usually also called homotopy groups, even though they are not groups in general.
are usually also called homotopy groups, even though they are not groups in general.
For each element 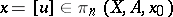 the mapping
the mapping 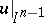 represents a mapping
represents a mapping 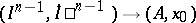 , and thus defines a certain element of the homotopy group
, and thus defines a certain element of the homotopy group 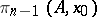 . This element depends only on
. This element depends only on  and is denoted by the symbol
and is denoted by the symbol 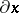 . The resulting mapping
. The resulting mapping 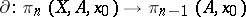 is a morphism of pointed sets (if
is a morphism of pointed sets (if 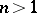 a homomorphism of groups) and is called a boundary homomorphism or a boundary operator. The boundary homomorphism, together with the homomorphisms
a homomorphism of groups) and is called a boundary homomorphism or a boundary operator. The boundary homomorphism, together with the homomorphisms 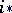 and
and 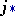 induced by the imbeddings
induced by the imbeddings 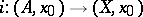 and
and 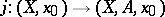 , makes it possible to write down a sequence of groups and homomorphisms, infinite from the left:
, makes it possible to write down a sequence of groups and homomorphisms, infinite from the left:
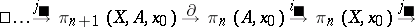 |
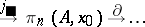 |
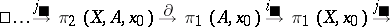 |
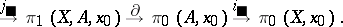 |
This is an exact sequence; it is called the exact homotopy sequence of the pair 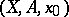 and is usually denoted by
and is usually denoted by 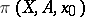 . If
. If 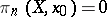 for all
for all 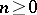 , then the homomorphism
, then the homomorphism 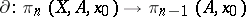 is an isomorphism (also for all
is an isomorphism (also for all  ).
).
The boundary homomorphism 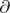 is natural, that is, it is a morphism of the functor
is natural, that is, it is a morphism of the functor 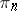 into the functor
into the functor  (more exactly, into the functor
(more exactly, into the functor 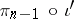 where
where 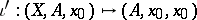 ). This makes it possible to define
). This makes it possible to define 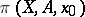 as a functor that takes values in the category of exact sequences of pointed sets which, except for the last six sets, are Abelian groups and, except for the last three sets, are groups.
as a functor that takes values in the category of exact sequences of pointed sets which, except for the last six sets, are Abelian groups and, except for the last three sets, are groups.
Let 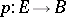 be an arbitrary fibration in the sense of Serre and let
be an arbitrary fibration in the sense of Serre and let 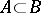 ,
, 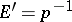 ,
, 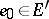 , and
, and 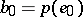 . The mapping
. The mapping 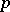 defines a mapping
defines a mapping 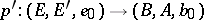 of pointed pairs. For any
of pointed pairs. For any 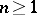 the induced homomorphism
the induced homomorphism 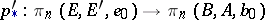 is an isomorphism. In particular, this is true for
is an isomorphism. In particular, this is true for  . In the latter case the formula
. In the latter case the formula 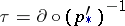 unambiguously defines a homomorphism
unambiguously defines a homomorphism 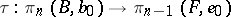 where
where 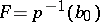 is the fibre of
is the fibre of  over
over  . This homomorphisms is called the homotopy transgression. It occurs in the exact sequence
. This homomorphisms is called the homotopy transgression. It occurs in the exact sequence
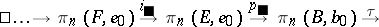 |
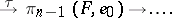 |
This sequence is called the homotopy sequence of the fibration 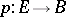 . Putting a fibration into correspondence with its homotopy sequence yields a functor on the category of all (pointed) fibrations.
. Putting a fibration into correspondence with its homotopy sequence yields a functor on the category of all (pointed) fibrations.
In the particular case when 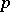 is the standard Serre fibration of paths over a space
is the standard Serre fibration of paths over a space 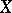 , for any
, for any 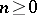 one has the isomorphism
one has the isomorphism 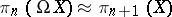 , where
, where 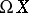 is the loop space of
is the loop space of 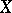 . This isomorphism is called the Hurewicz isomorphism.
. This isomorphism is called the Hurewicz isomorphism.
The above properties actually unambiguously define the homotopy groups 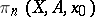 , i.e. may be taken as axioms which describe these groups. In fact, let
, i.e. may be taken as axioms which describe these groups. In fact, let 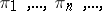 be an arbitrary sequence of homotopy-invariant normalized functors, defined on the category of pointed spaces, taking values in the category of pointed sets, and having the following property: For any fibration in the sense of Serre
be an arbitrary sequence of homotopy-invariant normalized functors, defined on the category of pointed spaces, taking values in the category of pointed sets, and having the following property: For any fibration in the sense of Serre 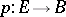 , any subset
, any subset 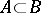 and any point
and any point 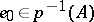 , the induced homomorphism
, the induced homomorphism 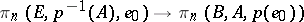 is an isomorphism. Such a sequence is called a homotopy system if for any
is an isomorphism. Such a sequence is called a homotopy system if for any 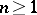 there is defined a morphism
there is defined a morphism 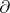 of the functor
of the functor 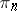 into the functor
into the functor 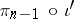 (if
(if 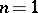 , into
, into 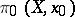 ) that is an isomorphism for any pointed pair
) that is an isomorphism for any pointed pair 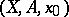 for which
for which 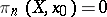 for all
for all 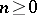 . Any homotopy system is isomorphic to the homotopy system constructed above, which consists of homotopy groups. Furthermore, if
. Any homotopy system is isomorphic to the homotopy system constructed above, which consists of homotopy groups. Furthermore, if 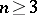 , a group structure can be uniquely introduced into the pointed sets
, a group structure can be uniquely introduced into the pointed sets 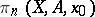 (and also into the sets
(and also into the sets 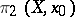 ) so that all morphisms
) so that all morphisms 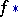 are homomorphism (this structure accordingly corresponds to that described by formula (1)). On the other hand, the sets
are homomorphism (this structure accordingly corresponds to that described by formula (1)). On the other hand, the sets 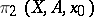 if
if 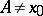 and
and 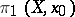 carry only the inverse group operation. All this means that the above properties unambiguously define the homotopy groups (up to the order of multiplication in non-commutative groups).
carry only the inverse group operation. All this means that the above properties unambiguously define the homotopy groups (up to the order of multiplication in non-commutative groups).
For any mapping 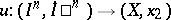 and any path
and any path 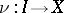 connecting two points
connecting two points 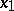 and
and 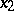 , the formula
, the formula 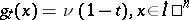 , defines a homotopy of
, defines a homotopy of 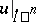 . By the homotopy extension axiom (cf. Cofibration) this homotopy can be extended to a homotopy
. By the homotopy extension axiom (cf. Cofibration) this homotopy can be extended to a homotopy 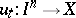 for which
for which 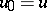 . The final mapping
. The final mapping 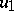 of this homotopy maps
of this homotopy maps  into
into 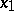 , i.e. represents a mapping
, i.e. represents a mapping 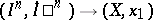 . The corresponding element of the homotopy group depends only on the class
. The corresponding element of the homotopy group depends only on the class 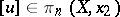 of
of  and the homotopy class
and the homotopy class 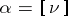 of
of  , and is denoted by the symbol
, and is denoted by the symbol 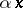 (if
(if 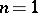 , by the symbol
, by the symbol 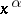 ). The family
). The family 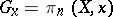 is thus defined as a local family on the space
is thus defined as a local family on the space 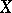 , i.e. on the fundamental groupoid of this space. In particular, for any point
, i.e. on the fundamental groupoid of this space. In particular, for any point 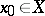 the group
the group 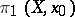 operates on
operates on 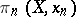 . If
. If  these operators act as inner automorphisms:
these operators act as inner automorphisms: 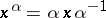 , and if
, and if 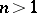 they make the group
they make the group 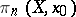 into a
into a 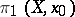 -module. For any continuous mapping
-module. For any continuous mapping 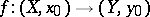 the induced homomorphisms
the induced homomorphisms 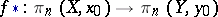 are operator homomorphisms (homomorphisms of modules):
are operator homomorphisms (homomorphisms of modules): 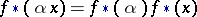 .
.
In a similar way, the groups 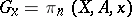 ,
, 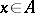 , constitute a local family of homotopy groups on the subspace
, constitute a local family of homotopy groups on the subspace 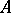 . In particular, the group
. In particular, the group 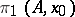 operates on the homotopy group
operates on the homotopy group 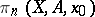 so that if
so that if 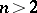 the group
the group 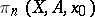 is a
is a 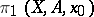 -module. The group
-module. The group 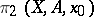 is said to be a crossed
is said to be a crossed 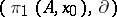 -module (cf. Crossed modules), where
-module (cf. Crossed modules), where 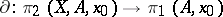 is the boundary homomorphism.
is the boundary homomorphism.
The group 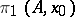 acts as a group of operators not only on the groups
acts as a group of operators not only on the groups  but also on the groups
but also on the groups 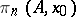 , and also, by virtue of the natural homomorphism
, and also, by virtue of the natural homomorphism 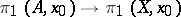 , on the groups
, on the groups  . With respect to these actions of
. With respect to these actions of  all homomorphisms of the exact sequence
all homomorphisms of the exact sequence 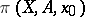 are operator homomorphisms, so that
are operator homomorphisms, so that 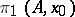 can be regarded as a group of operators on the sequence
can be regarded as a group of operators on the sequence  . This is equivalent to saying that the sequences
. This is equivalent to saying that the sequences 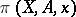 ,
, 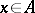 , constitute a local family of exact sequences of the subspace
, constitute a local family of exact sequences of the subspace 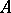 .
.
If the complement 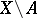 is represented as a union of disjoint open
is represented as a union of disjoint open  -dimensional cells, then the
-dimensional cells, then the 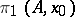 -module
-module 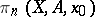 is a free module (if
is a free module (if 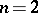 , a free crossed module) and has a system of free generators — a basis in bijective (not necessarily natural) correspondence with the cells of
, a free crossed module) and has a system of free generators — a basis in bijective (not necessarily natural) correspondence with the cells of 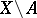 (Whitehead's theorem).
(Whitehead's theorem).
The mappings 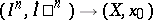 are in bijective correspondence with the mappings
are in bijective correspondence with the mappings 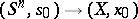 , where
, where 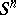 is an
is an  -dimensional sphere and
-dimensional sphere and 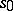 is some point on it. For this reason the elements of
is some point on it. For this reason the elements of 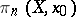 can be regarded as the homotopy classes of mappings
can be regarded as the homotopy classes of mappings 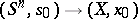 . This is also true if
. This is also true if 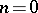 . The above identification depends on the selection of some relative homeomorphism
. The above identification depends on the selection of some relative homeomorphism 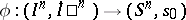 . It is common to select and fix the sphere
. It is common to select and fix the sphere 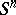 and the homeomorphism
and the homeomorphism 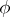 once and for all. In the original definition of Hurewicz, which is not frequently used nowadays,
once and for all. In the original definition of Hurewicz, which is not frequently used nowadays, 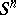 was not fixed, while
was not fixed, while 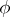 was given up to a homotopy. Such a specification of
was given up to a homotopy. Such a specification of 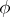 is equivalent to specifying an orientation on
is equivalent to specifying an orientation on 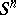 . Thus, according to Hurewicz, the elements of
. Thus, according to Hurewicz, the elements of 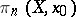 are pointed homotopy classes of mappings of an oriented
are pointed homotopy classes of mappings of an oriented  -dimensional sphere into
-dimensional sphere into 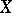 . The set
. The set 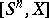 of non-pointed homotopy classes of mappings
of non-pointed homotopy classes of mappings 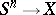 is in bijective correspondence with the orbits of the action of
is in bijective correspondence with the orbits of the action of 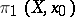 on
on 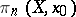 (cf. Orbit). If
(cf. Orbit). If 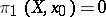 (or, more generally, if
(or, more generally, if 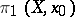 acts trivially on
acts trivially on 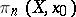 ), then
), then 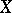 is said to be homotopically
is said to be homotopically  -simple. In this case
-simple. In this case 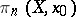 is independent of
is independent of 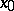 (so that the notation
(so that the notation 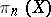 is fully justified). This group is naturally identified with the set
is fully justified). This group is naturally identified with the set 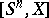 , which, as a consequence, has a group structure. A space that is homotopically
, which, as a consequence, has a group structure. A space that is homotopically  -simple for all
-simple for all  is said to be Abelian.
is said to be Abelian.
Let 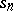 be the orientation class of the sphere
be the orientation class of the sphere 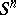 and let
and let 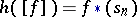 ,
,  . This defines a homomorphism
. This defines a homomorphism 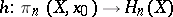 , the so-called Hurewicz homomorphism. Its kernel contains all elements of the form
, the so-called Hurewicz homomorphism. Its kernel contains all elements of the form 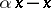 ,
, 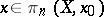 ,
, 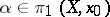 (if
(if 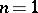 , all elements of the form
, all elements of the form 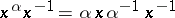 , i.e. it contains the commutator
, i.e. it contains the commutator 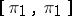 of
of 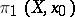 ). Poincaré's classical theorem states that for
). Poincaré's classical theorem states that for 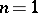 the kernel of
the kernel of 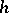 coincides with the commutator
coincides with the commutator 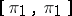 , so that the group
, so that the group 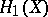 is isomorphic to the Abelianization of the fundamental group
is isomorphic to the Abelianization of the fundamental group 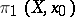 . Hurewicz's theorem, which is a generalization of Poincaré's theorem to the case
. Hurewicz's theorem, which is a generalization of Poincaré's theorem to the case 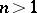 , states that if
, states that if 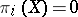 for
for 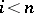 , then the homomorphism
, then the homomorphism 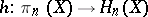 is an isomorphism (and the homomorphism
is an isomorphism (and the homomorphism 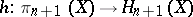 is an epimorphism).
is an epimorphism).
In a similar way, the elements of 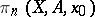 can be regarded as (pointed) homotopy classes of mappings
can be regarded as (pointed) homotopy classes of mappings 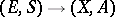 , where
, where 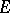 is an (oriented)
is an (oriented)  -dimensional ball and
-dimensional ball and 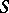 is its boundary. If the pair
is its boundary. If the pair 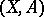 is homotopically
is homotopically  -simple (i.e. if
-simple (i.e. if 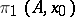 acts trivially on
acts trivially on 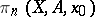 ), then the requirement of pointedness may be dropped in this definition. The formula
), then the requirement of pointedness may be dropped in this definition. The formula
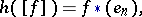 |
where 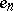 is the orientation class of the pair
is the orientation class of the pair 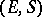 and
and 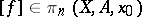 defines the Hurewicz homomorphism
defines the Hurewicz homomorphism
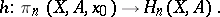 |
If 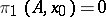 and
and 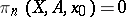 for
for 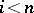 , this homomorphism is an isomorphism (Hurewicz's theorem for relative groups).
, this homomorphism is an isomorphism (Hurewicz's theorem for relative groups).
Two principal methods are known for the computation of the homotopy groups of specific spaces: the method of killing spaces (cf. Killing space) and the method of homotopy resolutions (cf. Homotopy type; Postnikov system). The first method is based on the isomorphism 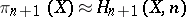 , which follows from Hurewicz's theorem and the definition of the killing space
, which follows from Hurewicz's theorem and the definition of the killing space 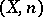 . This isomorphism reduces the computation of
. This isomorphism reduces the computation of 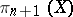 to the problem of computing the homology groups
to the problem of computing the homology groups 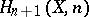 . The space
. The space 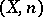 fibres over the space
fibres over the space 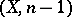 with fibre
with fibre 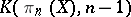 , and the homology groups of the space
, and the homology groups of the space 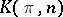 are known. Therefore one may try to find the lower homology groups of killing spaces by induction. The problem of computing the homology groups of a fibre space from the homology groups of its base and fibre is still not completely solved in its general formulation (and, obviously, a general satisfactory solution does not exist). However, extensive information on the homology groups of the spaces
are known. Therefore one may try to find the lower homology groups of killing spaces by induction. The problem of computing the homology groups of a fibre space from the homology groups of its base and fibre is still not completely solved in its general formulation (and, obviously, a general satisfactory solution does not exist). However, extensive information on the homology groups of the spaces 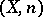 can be extracted from the corresponding Serre spectral sequence. In many cases this information is sufficient for the computation of
can be extracted from the corresponding Serre spectral sequence. In many cases this information is sufficient for the computation of 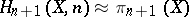 , at least for some
, at least for some  . An essential technical simplification of the problem is obtained on the basis of the Serre's theory of classes of Abelian groups and the
. An essential technical simplification of the problem is obtained on the basis of the Serre's theory of classes of Abelian groups and the 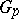 -approximation derived from it. With this theory it is possible to compute entirely in the cohomology and only for the coefficient groups
-approximation derived from it. With this theory it is possible to compute entirely in the cohomology and only for the coefficient groups 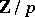 . The geometric principles on which this technique is based were first clarified by J.F. Adams and D. Sullivan on the basis of the concept of localization of topological spaces at a given prime number
. The geometric principles on which this technique is based were first clarified by J.F. Adams and D. Sullivan on the basis of the concept of localization of topological spaces at a given prime number 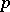 .
.
The second (also inductive) method of computing homotopy groups consists of a stepwise construction of the homotopy resolution of the space 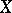 . Suppose the
. Suppose the  -th term of this resolution is known (e.g. if
-th term of this resolution is known (e.g. if 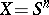 , then
, then 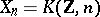 ). The next term must be the fibre space over
). The next term must be the fibre space over 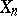 with fibre
with fibre 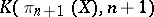 ; moreover, the group
; moreover, the group 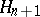 must be isomorphic to the known group
must be isomorphic to the known group 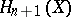 . This gives (on the basis of the corresponding spectral sequence) definite information on the group
. This gives (on the basis of the corresponding spectral sequence) definite information on the group 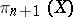 , which, in many cases, makes it possible to compute it completely. For example, for
, which, in many cases, makes it possible to compute it completely. For example, for 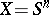 by this method all groups
by this method all groups 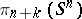 ,
, 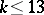 , can be found. In its modern form, this method is also based on the concept of localization.
, can be found. In its modern form, this method is also based on the concept of localization.
The method of homology resolutions was extended (cf. [4]) to an algorithm that is applicable to any simply-connected finite 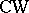 -complex and that gives all its homotopy groups. However, for practical use this algorithm is too complicated.
-complex and that gives all its homotopy groups. However, for practical use this algorithm is too complicated.
Since the homotopy theory is completely equivalent to the homotopy theory of simplicial sets, the definition of a homotopy group may be transferred to any (complete) simplicial set. The "combinatorial" definition obtained (due to D. Kan) can easily be extended to an algorithm. However, this algorithm is also too complicated for practical use.
From any of the above methods it is easy to establish that the homotopy groups of a simply-connected space having finitely-generated homology groups, are also finitely generated. The analogous statement for non-simply connected spaces (i.e. its homology groups should be finitely generated as 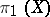 -modules) is, in general, not true.
-modules) is, in general, not true.
Let 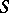 be the (reduced) suspension functor, and let
be the (reduced) suspension functor, and let  be the loop functor. Since these functors are adjoint, the identity mapping
be the loop functor. Since these functors are adjoint, the identity mapping 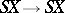 defines an imbedding
defines an imbedding 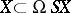 , for any
, for any 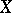 . Since
. Since 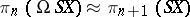 , this imbedding defines a homomorphism
, this imbedding defines a homomorphism
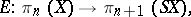 |
which is known as the suspension homomorphism. It coincides with the homomorphism obtained by assigning to an arbitrary (pointed) mapping 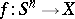 its suspension
its suspension 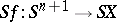 . This homomorphism occurs in an exact sequence:
. This homomorphism occurs in an exact sequence:
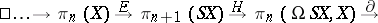 |
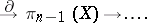 |
This sequence is called the suspension sequence of the space 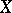 . The homomorphism
. The homomorphism 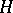 in it is a generalization of the classical Hopf invariant.
in it is a generalization of the classical Hopf invariant.
If 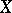 is a countable CW-complex with one vertex, the space
is a countable CW-complex with one vertex, the space 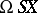 may be replaced by the infinite reduced product
may be replaced by the infinite reduced product 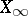 of the complex
of the complex 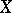 . This shows that if
. This shows that if 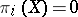 for
for 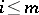 , then
, then 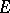 is an isomorphism for all
is an isomorphism for all 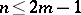 and an epimorphism if
and an epimorphism if 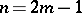 . This theorem is known as Freudenthal's suspension theorem (H. Freudenthal first published the proof for the case
. This theorem is known as Freudenthal's suspension theorem (H. Freudenthal first published the proof for the case 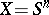 , although the theorem was known much earlier.)
, although the theorem was known much earlier.)
Freudenthal's theorem shows that for 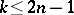 the group
the group 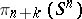 is independent of
is independent of  . It is called the
. It is called the 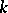 -th stable homotopy group of the sphere (cf. also Stable homotopy group). Similar stabilization phenomena occur for the homotopy groups of the orthogonal groups, of the Thom spaces
-th stable homotopy group of the sphere (cf. also Stable homotopy group). Similar stabilization phenomena occur for the homotopy groups of the orthogonal groups, of the Thom spaces 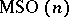 (cf. Thom space) and in many other cases. The general study of these phenomena is most conveniently done within the framework of the so-called theory of spectra. In this theory stable homotopy groups arise as the homotopy groups of spectra. These groups have an essentially simpler structure than the homotopy groups of a space and their study (and computation) is an easier task. For example, for the computation of these groups one has a special device: the Adams spectral sequence.
(cf. Thom space) and in many other cases. The general study of these phenomena is most conveniently done within the framework of the so-called theory of spectra. In this theory stable homotopy groups arise as the homotopy groups of spectra. These groups have an essentially simpler structure than the homotopy groups of a space and their study (and computation) is an easier task. For example, for the computation of these groups one has a special device: the Adams spectral sequence.
Homotopy groups have been generalized in various directions. For example, an attempt was made to replace the spheres by other spaces. Here one may note toroidal homotopy groups, obtained by interpreting the Whitehead product as a commutator. It was also shown that the set of homotopy classes of mappings 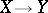 admits a group operation which is natural with respect to
admits a group operation which is natural with respect to 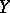 if and only if
if and only if 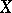 is a co-
is a co-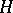 -space. Homotopy groups with coefficients were obtained by replacing the spheres
-space. Homotopy groups with coefficients were obtained by replacing the spheres 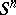 by the Moore spaces
by the Moore spaces 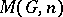 (cf. Moore space). This definition of homotopy groups with coefficients was not very successful. A more satisfactory definition (compatible with the general Eckmann–Hilton duality principle) was obtained by replacing the Moore
(cf. Moore space). This definition of homotopy groups with coefficients was not very successful. A more satisfactory definition (compatible with the general Eckmann–Hilton duality principle) was obtained by replacing the Moore 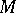 -spaces by co-
-spaces by co-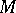 -spaces. However, these homotopy groups were not defined for all
-spaces. However, these homotopy groups were not defined for all 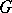 (e.g. for
(e.g. for 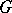 the additive group of real numbers, these groups are not defined).
the additive group of real numbers, these groups are not defined).
The question of the construction of homotopy groups in categories other than the category of pointed pairs has been studied in detail. First of all one has to mention the homotopy groups of a triad (cf. Triads, see, e.g., [3]), which were very useful in the study of the homomorphism 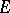 . A very general construction of homotopy groups was proposed in connection with studies on duality. On the basis of the concept of a standard construction (see [6]) the construction of homotopy groups was transferred to arbitrary categories. A fundamental role in this construction is played by the homotopy groups of simplicial sets mentioned earlier.
. A very general construction of homotopy groups was proposed in connection with studies on duality. On the basis of the concept of a standard construction (see [6]) the construction of homotopy groups was transferred to arbitrary categories. A fundamental role in this construction is played by the homotopy groups of simplicial sets mentioned earlier.
References
| [1] | N.E. Steenrod, "The topology of fibre bundles" , Princeton Univ. Press (1951) |
| [2] | V.G. Boltyanskii, "The homotopy theory of continuous mapping and vector fields" , Moscow (1955) (In Russian) |
| [3] | S.-T. Hu, "Homotopy theory" , Acad. Press (1959) |
| [4] | E.H. Brown, "Finite computability of Postnikov complexes" Ann. of Math. (2) , 65 (1957) pp. 1–20 |
| [5] | D. Kan, "A combinatorial definition of homotopy groups" Ann. of Math. (2) , 67 (1958) pp. 282–313 |
| [6] | J. Stallings, "A finitely presented group whose 3-dimensional integral homology is not finitely generated" Amer. J. Math. , 85 (1963) pp. 541–543 |
| [7a] | B. Eckmann, P. Hilton, "Groupes d'homotopie et dualité. Groupes absolus" C.R. Acad. Sci. , 246 (1958) pp. 2444–2447 |
| [7b] | B. Eckmann, P. Hilton, "Groupes d'homotopie et dualité. Suites exactes" C.R. Acad. Sci. , 246 (1958) pp. 2555–2558 |
| [7c] | B. Eckmann, P. Hilton, "Groupes d'homotopie et dualité. Coefficients" C.R. Acad. Sci. , 246 (1958) pp. 2991–2993 |
| [7d] | B. Eckmann, P. Hilton, "Transgression homotopique et cohomologique" C.R. Acad. Sci. , 247 (1958) pp. 620–623 |
| [7e] | B. Eckmann, P. Hilton, "Décomposition homologique d'une polyèdre simplement connexe" C.R. Acad. Sci. , 248 (1959) pp. 2054–2056 |
| [8] | D. Sullivan, "Geometric topology" , M.I.T. (1971) (Notes) |
Comments
Although W. Hurewicz
was the first to study the higher homotopy groups in detail, the definition was in fact suggested a few years earlier by E. Čech [a2]. The action of the fundamental group on the higher homotopy groups was first studied by S. Eilenberg [a3]. A good general reference for homotopy groups is [a4].
The stable homotopy groups form a generalized homology theory, i.e. a theory which satisfies all the Eilenberg–Steenrod axioms except possibly the dimension axiom. This theory is in fact defined by the spectrum of spheres 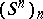 , cf. Spectrum of spaces. The corresponding generalized cohomology theory (cf. Generalized cohomology theories) defined by this spectrum consists of the cohomotopy group. Cf., e.g., [a4] and [a11] for more details. Powerful tools for computing the stable homotopy groups of the spheres (besides the (classical) Adams spectral sequence) involve the Adams–Novikov spectral sequence, the so-called chromatic spectral sequence and complex cobordism, cf. [a12].
, cf. Spectrum of spaces. The corresponding generalized cohomology theory (cf. Generalized cohomology theories) defined by this spectrum consists of the cohomotopy group. Cf., e.g., [a4] and [a11] for more details. Powerful tools for computing the stable homotopy groups of the spheres (besides the (classical) Adams spectral sequence) involve the Adams–Novikov spectral sequence, the so-called chromatic spectral sequence and complex cobordism, cf. [a12].
References
| [a1a] | W. Hurewicz, "Beiträge zur Topologie der Deformationen I-II" Proc. Ned. Akad. Weten. Ser. A , 38 (1935) pp. 112–119; 521–528 |
| [a1b] | W. Hurewicz, "Beiträge zur Topologie der Deformationen III-IV" Proc. Ned. Akad. Weten. Ser. A , 39 (1936) pp. 117–126; 215–224 |
| [a2] | E. Čech, "Höherdimensionale Homotopiegruppen" , Verh. Intern. Mathematikerkongress Zürich, 1932 , O. Füssli (1932) pp. 203 |
| [a3] | S. Eilenberg, "On the relation between the fundamental group of a space and the higher homotopy groups" Fund. Math. , 32 (1939) pp. 167–175 |
| [a4] | G.W. Whitehead, "Elements of homotopy theory" , Springer (1978) pp. 23; 415–455 |
| [a5] | B. Gray, "Homotopy theory. An introduction to algebraic topology" , Acad. Press (1975) pp. §12 |
| [a6] | P.J. Hilton, "An introduction to homotopy theory" , Cambridge Univ. Press (1953) |
| [a7] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1960) |
| [a8] | D. Sullivan, "Genetics of homotopy theory and the Adams conjecture" Ann. of Math. , 100 (1974) pp. 1–79 |
| [a9] | D.G. Quillen, "Homotopical algebra" , Springer (1967) |
| [a10] | B. Eckmann, "Homotopie et dualité" , Coll. Topol. Algébrique Louvain, 1956 , Masson (1957) pp. 41–53 |
| [a11] | R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975) |
| [a12] | D.C. Ravenel, "Complex cobordism and stable homotopy groups of spheres" , Acad. Press (1986) |
Homotopy group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homotopy_group&oldid=14008