Hilbert space
A vector space 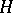 over the field of complex (or real) numbers, together with a complex-valued (or real-valued) function
over the field of complex (or real) numbers, together with a complex-valued (or real-valued) function 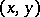 defined on
defined on 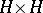 , with the following properties:
, with the following properties:
1) 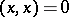 if and only if
if and only if 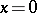 ;
;
2) 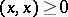 for all
for all 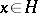 ;
;
3) 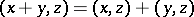 ,
, 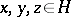 ;
;
4) 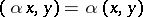 ,
, 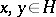 ,
, 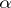 a complex (or real) number;
a complex (or real) number;
5) 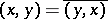 ,
, 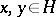 ;
;
6) if 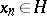 ,
, 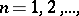 and if
and if
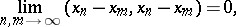 |
then there exists an element 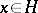 such that
such that
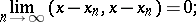 |
the element  is called the limit of the sequence
is called the limit of the sequence 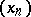 ;
;
7) 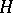 is an infinite-dimensional vector space.
is an infinite-dimensional vector space.
The function 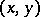 which satisfies axioms 1)–5) is called the scalar (or inner) product of
which satisfies axioms 1)–5) is called the scalar (or inner) product of  and
and 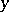 . The magnitude
. The magnitude 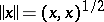 is said to be the norm (or the length) of
is said to be the norm (or the length) of 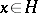 . The inequality
. The inequality  is valid. If a distance between elements
is valid. If a distance between elements  is introduced in
is introduced in  by means of the equality
by means of the equality 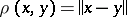 ,
,  is converted into a metric space.
is converted into a metric space.
Two Hilbert spaces  and
and 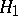 are said to be isomorphic (or isometrically isomorphic) if there exists a one-to-one correspondence
are said to be isomorphic (or isometrically isomorphic) if there exists a one-to-one correspondence  ,
,  ,
,  , between
, between 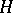 and
and  which preserves the linear operations and the scalar product.
which preserves the linear operations and the scalar product.
Hilbert spaces constitute the class of infinite-dimensional vector spaces that are most often used and that are the most important as far as applications are concerned. They are the natural extension of the concept of a finite-dimensional vector space with a scalar product (i.e. a finite-dimensional Euclidean space or a finite-dimensional unitary space). In fact, if a scalar product is specified in a finite-dimensional vector space (over the field of real or complex numbers), then property 6), which is called the completeness of the Hilbert space, is automatically satisfied. Infinite-dimensional vector spaces 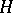 with a scalar product are known as pre-Hilbert spaces; there exist pre-Hilbert spaces for which property 6) does not hold. Any pre-Hilbert space can be completed to a Hilbert space.
with a scalar product are known as pre-Hilbert spaces; there exist pre-Hilbert spaces for which property 6) does not hold. Any pre-Hilbert space can be completed to a Hilbert space.
In the definition of a Hilbert space the condition of infinite dimensionality is often omitted, i.e. a pre-Hilbert space is understood to mean a vector space over the field of complex (or real) numbers with a scalar product, while a Hilbert space is the name given to a complete pre-Hilbert space.
Examples of Hilbert spaces.
1) The complex space 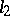 (or
(or 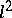 ). The elements of this Hilbert space are infinite sequences of complex numbers
). The elements of this Hilbert space are infinite sequences of complex numbers 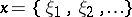 ,
,  that are square summable:
that are square summable:
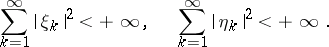 |
The scalar product is defined by the equation
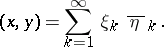 |
2) The space  (a generalization of Example 1)). Let
(a generalization of Example 1)). Let 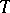 be an arbitrary set. The elements of the Hilbert space
be an arbitrary set. The elements of the Hilbert space 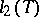 are complex-valued functions
are complex-valued functions 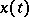 on
on 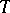 differing from zero in at most countably many points
differing from zero in at most countably many points 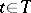 and such that the series
and such that the series
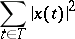 |
converges. The scalar product is defined by the equation
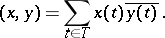 |
Any Hilbert space is isomorphic to the space  for some suitably chosen
for some suitably chosen 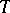 .
.
3) The space 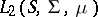 (or
(or 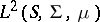 ) of complex-valued functions
) of complex-valued functions 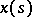 defined on a set
defined on a set  with a totally-additive positive measure
with a totally-additive positive measure 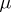 (given on the
(given on the 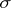 -algebra of subsets
-algebra of subsets  of
of 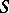 ) which are measurable and have an integrable square modulus:
) which are measurable and have an integrable square modulus:
 |
In this Hilbert space the scalar product is defined by:
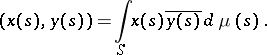 |
4) The Sobolev space  , which is also denoted by
, which is also denoted by  (cf. Imbedding theorems).
(cf. Imbedding theorems).
5) A Hilbert space of functions with values in a Hilbert space. Let 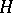 be some Hilbert space with scalar product
be some Hilbert space with scalar product 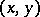 ,
, 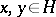 . Further, let
. Further, let  be an arbitrary domain in
be an arbitrary domain in 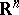 , and let
, and let  ,
, 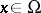 , be a function with values in
, be a function with values in 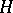 that is Bochner-measurable (cf. Bochner integral) and is such that
that is Bochner-measurable (cf. Bochner integral) and is such that
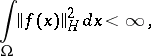 |
where 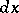 is Lebesgue measure on
is Lebesgue measure on  (instead of Lebesgue measure one may take any other positive countably-additive measure). If one defines the scalar product
(instead of Lebesgue measure one may take any other positive countably-additive measure). If one defines the scalar product
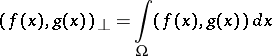 |
on this set of functions, a new Hilbert space 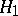 is obtained.
is obtained.
6) The set of continuous Bohr almost-periodic functions on the real line forms a pre-Hilbert space if the scalar product is defined by
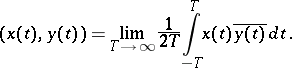 |
The existence of the limit follows from the theory of almost-periodic functions. This space is completed to the class  of Besicovitch almost-periodic functions.
of Besicovitch almost-periodic functions.
The spaces 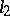 and
and 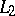 were introduced and studied by D. Hilbert [1] in his fundamental work on the theory of integral equations and infinite quadratic forms. The definition of a Hilbert space was given by J. von Neumann [3], F. Riesz [4] and M.H. Stone [13], who also laid the basis for their systematic study.
were introduced and studied by D. Hilbert [1] in his fundamental work on the theory of integral equations and infinite quadratic forms. The definition of a Hilbert space was given by J. von Neumann [3], F. Riesz [4] and M.H. Stone [13], who also laid the basis for their systematic study.
A Hilbert space is a natural extension of the ordinary three-dimensional space in Euclidean geometry, and many geometric concepts have their interpretation in a Hilbert space, so that one is entitled to speak about the geometry of Hilbert space. Two vectors  and
and 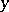 from a Hilbert space
from a Hilbert space 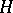 are said to be orthogonal
are said to be orthogonal 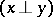 if
if 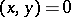 . Two linear subspaces
. Two linear subspaces  and
and 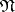 in
in 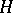 are said to be orthogonal
are said to be orthogonal 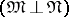 if each element of
if each element of  is orthogonal to each element from
is orthogonal to each element from 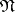 . The orthogonal complement of a set
. The orthogonal complement of a set  is the set
is the set 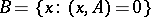 , i.e. the set of elements
, i.e. the set of elements 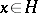 which are orthogonal to all elements of
which are orthogonal to all elements of 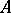 . It is denoted by
. It is denoted by 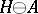 or, if
or, if 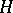 is understood, by
is understood, by 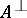 . The orthogonal complement
. The orthogonal complement 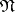 of an arbitrary set
of an arbitrary set 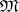 in
in 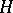 is a closed linear subspace. If
is a closed linear subspace. If 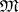 is a closed linear subspace in a Hilbert space (which may also be referred to as a Hilbert subspace), then any element
is a closed linear subspace in a Hilbert space (which may also be referred to as a Hilbert subspace), then any element 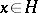 can be uniquely represented as the sum
can be uniquely represented as the sum 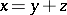 ,
,  ,
,  . This decomposition is known as the theorem on orthogonal complements and is usually written as
. This decomposition is known as the theorem on orthogonal complements and is usually written as
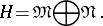 |
A set 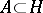 is said to be an orthonormal set or an orthonormal system if any two different vectors from
is said to be an orthonormal set or an orthonormal system if any two different vectors from 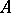 are orthogonal and if the norm of each vector
are orthogonal and if the norm of each vector 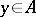 is equal to one. An orthonormal set is said to be a complete orthonormal set if there is no non-zero vector from
is equal to one. An orthonormal set is said to be a complete orthonormal set if there is no non-zero vector from 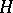 that is orthogonal to all the vectors of this set. If
that is orthogonal to all the vectors of this set. If 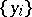 is an orthonormal sequence and
is an orthonormal sequence and 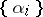 is a sequence of scalars, then the series
is a sequence of scalars, then the series
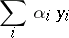 |
converges if and only if
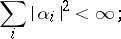 |
moreover
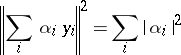 |
(Pythagoras' theorem in Hilbert spaces).
Let  be an orthonormal set in a Hilbert space
be an orthonormal set in a Hilbert space 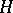 and let
and let  be an arbitrary vector from
be an arbitrary vector from  . Then
. Then 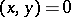 for all
for all 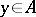 , with the exception of a finite or countable set of vectors. The series
, with the exception of a finite or countable set of vectors. The series
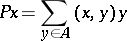 |
converges, and its sum is independent of the order of its non-zero terms. The operator 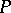 is the orthogonal projection operator, or projector, on the (closed) Hilbert subspace generated by
is the orthogonal projection operator, or projector, on the (closed) Hilbert subspace generated by 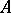 .
.
A set 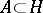 is said to be an orthonormal basis of a linear subspace
is said to be an orthonormal basis of a linear subspace 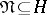 if
if 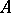 is contained in
is contained in  and if the equality
and if the equality
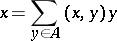 |
is valid for any 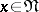 , i.e. if any vector
, i.e. if any vector 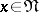 can be expanded with respect to the system
can be expanded with respect to the system 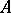 , that is, can be represented with the aid of vectors from
, that is, can be represented with the aid of vectors from 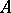 . The set of numbers
. The set of numbers 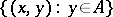 is called the set of Fourier coefficients of the element
is called the set of Fourier coefficients of the element  with respect to the basis
with respect to the basis 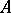 . Each subspace of a Hilbert space
. Each subspace of a Hilbert space 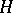 (in particular,
(in particular, 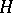 itself) has an orthonormal basis.
itself) has an orthonormal basis.
An orthonormal basis in 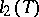 is a set of functions
is a set of functions 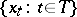 defined by the formula
defined by the formula 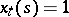 if
if  and
and 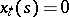 if
if  . In a space
. In a space 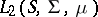 the expansion of a vector with respect to a basis takes the form of an expansion with respect to a system of orthogonal functions; this represents an important method for solving problems in mathematical physics.
the expansion of a vector with respect to a basis takes the form of an expansion with respect to a system of orthogonal functions; this represents an important method for solving problems in mathematical physics.
For an orthonormal set 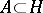 the following statements are equivalent:
the following statements are equivalent:  is complete;
is complete;  is an orthonormal basis for
is an orthonormal basis for 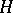 ; and
; and  for any
for any  .
.
All orthonormal bases of a given Hilbert space have the same cardinality. This fact makes it possible to define the dimension of a Hilbert space. In fact, the dimension of a Hilbert space is the cardinality of an arbitrary orthonormal basis in it. This dimension is sometimes referred to as the Hilbert dimension (as distinct from the linear dimension of a Hilbert space, i.e. the cardinality of the Hamel basis (cf. Basis) — a concept which does not take into account the topological structure of the Hilbert space). Two Hilbert spaces are isomorphic if and only if their dimensions are equal. The concept of a dimension is connected with that of the deficiency of a Hilbert subspace, also called the codimension of a Hilbert subspace. In fact, the codimension of a Hilbert subspace 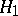 of a Hilbert space
of a Hilbert space 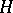 is the dimension of the orthogonal complement
is the dimension of the orthogonal complement 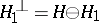 . A Hilbert subspace with codimension equal to one, i.e. the orthogonal complement to which is one-dimensional, is known as a hyperspace. A translate of a hyperspace is called a hyperplane.
. A Hilbert subspace with codimension equal to one, i.e. the orthogonal complement to which is one-dimensional, is known as a hyperspace. A translate of a hyperspace is called a hyperplane.
Some of the geometrical concepts involve the use of the terminology of linear operators in a Hilbert space; they include, in particular, the concept of an opening of linear subspaces. The opening of two subspaces 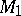 and
and 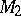 in a Hilbert space
in a Hilbert space 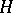 is the norm
is the norm 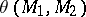 of the difference of the operators which project
of the difference of the operators which project 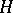 on the closure of these linear subspaces.
on the closure of these linear subspaces.
The simplest properties of an opening are:
a)  ;
;
b) 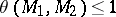 , and, in the case of strict inequality,
, and, in the case of strict inequality, 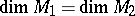 .
.
Many problems in Hilbert spaces involve only finite sets of vectors of a Hilbert space, i.e. elements of finite-dimensional linear subspaces of a Hilbert space. This is why the concepts and methods of linear algebra play an important role in the theory of Hilbert spaces. Vectors 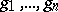 in a Hilbert space are said to be linearly independent if the equation
in a Hilbert space are said to be linearly independent if the equation
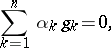 |
where 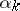 are scalars, holds only if all
are scalars, holds only if all 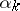 are equal to zero. Vectors are linearly independent if their Gram determinant does not vanish. A countable sequence of vectors
are equal to zero. Vectors are linearly independent if their Gram determinant does not vanish. A countable sequence of vectors  is said to be a linearly independent sequence if all its finite subsets are linearly independent. Each linearly independent sequence can be orthonormalized, i.e. it is possible to construct an orthonormal system
is said to be a linearly independent sequence if all its finite subsets are linearly independent. Each linearly independent sequence can be orthonormalized, i.e. it is possible to construct an orthonormal system 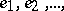 such that for all
such that for all  the linear hulls (cf. Linear hull) of the sets
the linear hulls (cf. Linear hull) of the sets 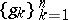 and
and 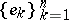 coincide. This construction is known as the Gram–Schmidt orthogonalization (orthonormalization) process and consists of the following:
coincide. This construction is known as the Gram–Schmidt orthogonalization (orthonormalization) process and consists of the following:
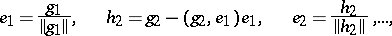 |
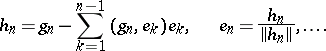 |
Operations of direct sum and tensor product are defined in the set of Hilbert spaces. The direct sum of Hilbert spaces 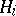 ,
, 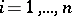 , where each
, where each 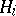 has a corresponding scalar product, is the Hilbert space
has a corresponding scalar product, is the Hilbert space
 |
defined as follows: In the vector space 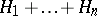 — the direct sum of the vector spaces
— the direct sum of the vector spaces  — the scalar product is defined by
— the scalar product is defined by
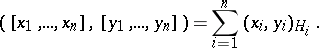 |
If 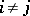 , the elements of
, the elements of 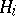 and
and 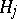 in the direct sum
in the direct sum
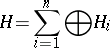 |
are mutually orthogonal, and the projection of  onto
onto 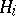 coincides with the orthogonal projection of
coincides with the orthogonal projection of 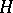 onto
onto 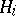 . The concept of the direct sum of Hilbert spaces has been generalized to the case of an infinite set of direct components. Let a Hilbert space
. The concept of the direct sum of Hilbert spaces has been generalized to the case of an infinite set of direct components. Let a Hilbert space 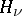 be specified for each
be specified for each  of some index set
of some index set 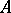 . The direct sum of Hilbert spaces (denoted by
. The direct sum of Hilbert spaces (denoted by 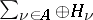 ) is the set
) is the set 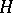 of all functions
of all functions 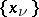 defined on
defined on 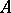 such that
such that 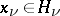 for each
for each 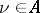 , and
, and 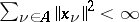 . The linear operations in
. The linear operations in 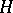 are defined by
are defined by
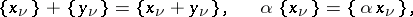 |
while the scalar product is defined by
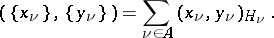 |
If the linear operations and the scalar product are defined in this manner, the direct sum
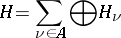 |
becomes a Hilbert space.
Another important operation in the set of Hilbert spaces is the tensor product. The tensor product of Hilbert spaces 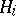 ,
, 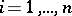 , is defined as follows. Let
, is defined as follows. Let 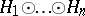 be the tensor product of the vector spaces
be the tensor product of the vector spaces 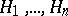 . In the vector space
. In the vector space 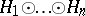 there exists a unique scalar product such that
there exists a unique scalar product such that
 |
for all 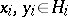 . Thus, the vector space becomes a pre-Hilbert space, whose completion is a Hilbert space, denoted by
. Thus, the vector space becomes a pre-Hilbert space, whose completion is a Hilbert space, denoted by 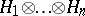 , or
, or 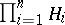 , and is known as the tensor product of the Hilbert spaces
, and is known as the tensor product of the Hilbert spaces 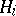 .
.
Hilbert spaces form an important class of Banach spaces; any Hilbert space 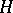 is a Banach space with respect to the norm
is a Banach space with respect to the norm 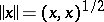 , and the following parallelogram identity holds for any two vectors
, and the following parallelogram identity holds for any two vectors 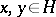 :
:
 |
The parallelogram identity distinguishes the class of Hilbert spaces from the Banach spaces, viz. if the parallelogram identity is valid in a real normed space 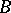 for any pair of elements
for any pair of elements 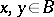 , then the function
, then the function
 |
satisfies the axioms of a scalar product, and thus makes 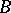 into a pre-Hilbert space (if
into a pre-Hilbert space (if 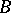 is a Banach space, it is made a Hilbert space). From the parallelogram identity it follows that every Hilbert space is a uniformly-convex space. As in any Banach space, two topologies may be specified in a Hilbert space — a strong (norm) one and a weak one. These topologies are different. A Hilbert space is separable in the strong topology if and only if it is separable in the weak topology; a convex set (in particular, a linear subspace) in a Hilbert space is strongly closed if and only if it is weakly closed.
is a Banach space, it is made a Hilbert space). From the parallelogram identity it follows that every Hilbert space is a uniformly-convex space. As in any Banach space, two topologies may be specified in a Hilbert space — a strong (norm) one and a weak one. These topologies are different. A Hilbert space is separable in the strong topology if and only if it is separable in the weak topology; a convex set (in particular, a linear subspace) in a Hilbert space is strongly closed if and only if it is weakly closed.
As in the theory of general Banach spaces, so, too, in the theory of Hilbert spaces, the concept of separability plays an important role. A Hilbert space is separable if and only if it has countable dimension. The Hilbert spaces 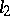 and
and 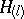 are separable; the Hilbert space
are separable; the Hilbert space 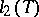 is separable if and only if
is separable if and only if 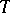 is at most countable; a Hilbert space
is at most countable; a Hilbert space 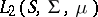 is separable if the measure
is separable if the measure 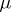 has a countable basis. The Hilbert space
has a countable basis. The Hilbert space 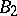 is not separable.
is not separable.
Any orthonormal basis in a separable Hilbert space 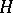 is at the same time an unconditional Schauder basis in
is at the same time an unconditional Schauder basis in 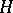 , regarded as a Banach space. However, non-orthogonal Schauder bases also exist in separable Hilbert spaces. Accordingly, the following theorem is valid [7]: Let
, regarded as a Banach space. However, non-orthogonal Schauder bases also exist in separable Hilbert spaces. Accordingly, the following theorem is valid [7]: Let 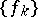 be a complete system of vectors in a Hilbert space
be a complete system of vectors in a Hilbert space 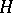 and let
and let 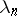 and
and 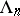 be the smallest and the largest eigen values of the Gram matrix
be the smallest and the largest eigen values of the Gram matrix
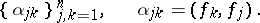 |
If
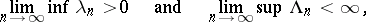 |
then 1) the sequence 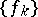 is a basis in
is a basis in 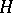 ; and 2) there exists a sequence
; and 2) there exists a sequence 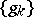 biorthogonal to
biorthogonal to 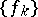 which is also a basis in
which is also a basis in 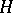 .
.
As in any Banach space, the description of the set of linear functionals on a Hilbert space and the study of the properties of these functionals is very important. Linear functionals on Hilbert spaces have a particularly simple structure. Any linear functional 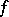 on a Hilbert space
on a Hilbert space 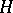 can be uniquely denoted by
can be uniquely denoted by 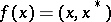 for all
for all 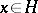 , where
, where 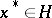 ; moreover
; moreover 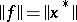 . The space
. The space 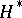 of linear functionals
of linear functionals 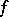 on
on 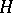 is isometrically anti-isomorphic to
is isometrically anti-isomorphic to 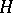 (i.e. the correspondence
(i.e. the correspondence 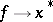 is isometric, additive and anti-homogeneous:
is isometric, additive and anti-homogeneous: 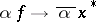 ). In particular, a Hilbert space is reflexive (cf. Reflexive space), and for this reason the following statements are valid: a Hilbert space is weakly sequentially complete; a subset of a Hilbert space is relatively weakly compact if and only if it is bounded.
). In particular, a Hilbert space is reflexive (cf. Reflexive space), and for this reason the following statements are valid: a Hilbert space is weakly sequentially complete; a subset of a Hilbert space is relatively weakly compact if and only if it is bounded.
The main content of the theory of Hilbert spaces is the theory of linear operators on them. The concept of a Hilbert space itself was formulated in the works of Hilbert [2] and E. Schmidt [14] on the theory of integral equations, while the abstract definition of a Hilbert space was given by von Neumann [3], F. Riesz [4] and Stone [13] in their studies of Hermitian operators. The theory of operators on a Hilbert space is a fundamental branch of the general theory of operators for two reasons.
First, the theory of self-adjoint and unitary operators on a Hilbert space is not only one of the most developed parts of the general theory of linear operators, but is also of wide use in other parts of functional analysis and in a number of other parts of mathematics and physics. The theory of linear operators on a Hilbert space makes it possible to look at various problems in mathematical physics from a unified point of view; above all, these are the questions concerning eigen values and eigen functions. Moreover, the theory of self-adjoint operators on a Hilbert space is a mathematical tool in quantum mechanics: In the description of a quantum-mechanical system, the observed quantities (energy, momentum, position, etc.) are interpreted as self-adjoint operators on some Hilbert space, while the states of the system are elements of that space. In turn, the problems of quantum mechanics have up to our time an influence on the development of the theory of self-adjoint operators, and also on the theory of operator algebras on Hilbert spaces.
Secondly, the intensively developed theory of self-adjoint operators (cf. Self-adjoint operator) on a Hilbert space (in particular, that of cyclic, nilpotent, cellular, contractible, spectral, and scalar operators) is an important model of the theory of linear operators on more general spaces.
An important class of linear operators on a Hilbert space is formed by the everywhere-defined continuous operators, also called bounded operators. If one introduces on the set 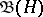 of bounded linear operators on
of bounded linear operators on 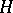 the operations of addition, multiplication by a scalar and multiplication of operators, as well as the norm of an operator, by the usual rules (see Linear operator) and defines the involution in
the operations of addition, multiplication by a scalar and multiplication of operators, as well as the norm of an operator, by the usual rules (see Linear operator) and defines the involution in 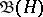 as transition to the adjoint operator, then
as transition to the adjoint operator, then 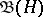 becomes a Banach algebra with involution. Important classes of bounded operators on a Hilbert space are the self-adjoint operators, the unitary operators and the normal operators (cf. Self-adjoint operator; Unitary operator; Normal operator), since they have special properties with respect to the scalar product. These classes of operators are well-studied; the fundamental instruments in their study are the simplest bounded self-adjoint operators, such as the operators of orthogonal projection, or simply projectors (cf. Projector). The means by which any self-adjoint, unitary or normal operator on a complex Hilbert space is constructed from projectors, is given by the spectral decomposition of a linear operator, which is especially simple in the case of a separable Hilbert space.
becomes a Banach algebra with involution. Important classes of bounded operators on a Hilbert space are the self-adjoint operators, the unitary operators and the normal operators (cf. Self-adjoint operator; Unitary operator; Normal operator), since they have special properties with respect to the scalar product. These classes of operators are well-studied; the fundamental instruments in their study are the simplest bounded self-adjoint operators, such as the operators of orthogonal projection, or simply projectors (cf. Projector). The means by which any self-adjoint, unitary or normal operator on a complex Hilbert space is constructed from projectors, is given by the spectral decomposition of a linear operator, which is especially simple in the case of a separable Hilbert space.
A more complex branch of the theory of linear operators on a Hilbert space is the theory of unbounded operators. The most important unbounded operators on a Hilbert space are the closed linear operators with a dense domain of definition; in particular, unbounded self-adjoint and normal operators. Between the self-adjoint and the unitary operators on a Hilbert space there is a one-to-one relation, defined by the Cayley transformation (cf. Cayley transform). Of importance (especially in the theory of linear differential operators) is the class of symmetric operators (cf. Symmetric operator) on a Hilbert space, and the theory of self-adjoint extensions of such operators.
Unbounded self-adjoint and normal operators on a complex Hilbert space 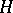 also have a spectral decomposition. The spectral decomposition is the greatest achievement of the theory of self-adjoint and normal operators on a Hilbert space. It corresponds to the classical reduction theory of Hermitian and normal complex matrices on an
also have a spectral decomposition. The spectral decomposition is the greatest achievement of the theory of self-adjoint and normal operators on a Hilbert space. It corresponds to the classical reduction theory of Hermitian and normal complex matrices on an  -dimensional unitary space. Namely, the spectral decomposition and the operator calculus for self-adjoint and normal operators which is related to it ensure a wide range of applications in various parts of mathematics for the theory of operators on a Hilbert space.
-dimensional unitary space. Namely, the spectral decomposition and the operator calculus for self-adjoint and normal operators which is related to it ensure a wide range of applications in various parts of mathematics for the theory of operators on a Hilbert space.
For bounded self-adjoint operators on 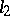 the spectral decomposition was found by Hilbert [1], who also introduced the important concept of a resolution of the identity for a self-adjoint operator. Nowadays, several approaches to the spectral theory of self-adjoint and normal operators are available. One of the most profound is given by the theory of Banach algebras. The spectral decomposition of an unbounded self-adjoint operator was found by von Neumann [3]. His work preceded the important investigations of T. Carleman [8], who obtained the spectral decomposition for the case of a symmetric integral operator, and who also discovered that there is no complete analogy between symmetric bounded and unbounded operators. The importance of the concept of a self-adjoint operator was first drawn attention to by Schmidt (cf. [3]).
the spectral decomposition was found by Hilbert [1], who also introduced the important concept of a resolution of the identity for a self-adjoint operator. Nowadays, several approaches to the spectral theory of self-adjoint and normal operators are available. One of the most profound is given by the theory of Banach algebras. The spectral decomposition of an unbounded self-adjoint operator was found by von Neumann [3]. His work preceded the important investigations of T. Carleman [8], who obtained the spectral decomposition for the case of a symmetric integral operator, and who also discovered that there is no complete analogy between symmetric bounded and unbounded operators. The importance of the concept of a self-adjoint operator was first drawn attention to by Schmidt (cf. [3]).
Note that both for the investigations by Hilbert, and for much later investigations, the works of P.L. Chebyshev, A.A. Markov and Th.J. Stieltjes on the classical problems of moments, Jacobi matrices and continued fractions (cf. [9]) were of great importance (cf. Continued fraction; Jacobi matrix; Moment problem).
References
| [1] | D. Hilbert, "Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen" , Chelsea, reprint (1953) |
| [2] | A.S. Besicovitch, "Almost periodic functions" , Cambridge Univ. Press (1932) |
| [3] | J. von Neumann, "Allgemeine Eigenwerttheorie Hermitischer Funktionaloperatoren" Math. Ann. , 102 (1929) pp. 49–131 |
| [4] | F. Riesz, "Ueber die linearen Transformationen des komplexen Hilbertschen Raumes" Acta. Sci. Math. Szeged , 5 : 1 (1930) pp. 23–54 |
| [5] | J.A. Dieudonné, "Foundations of modern analysis" , Acad. Press (1961) (Translated from French) |
| [6] | N. Bourbaki, "Elements of mathematics. Topological vector spaces" , Addison-Wesley (1977) (Translated from French) |
| [7] | N.I. [N.I. Akhiezer] Achieser, I.M. [I.M. Glaz'man] Glasman, "Theorie der linearen Operatoren im Hilbert Raum" , Akademie Verlag (1954) (Translated from Russian) |
| [8] | T. Carleman, "Sur les équations intégrales singulières à noyau réel et symmétrique" Univ. Årsskrift : 3 , Uppsala (1923) |
| [9] | N.I. Akhiezer, "The classical moment problem and some related questions in analysis" , Oliver & Boyd (1965) (Translated from Russian) |
| [10] | N. Dunford, J.T. Schwartz, "Linear operators" , 1–3 , Interscience (1958–1971) |
| [11] | F. Riesz, B. Szökefalvi-Nagy, "Functional analysis" , F. Ungar (1955) (Translated from French) |
| [12] | M.A. Naimark, "Lineare Differentialoperatoren" , Akademie Verlag (1960) (Translated from Russian) |
| [13] | M.H. Stone, "Linear transformations in Hilbert space and their applications to analysis" , Amer. Math. Soc. (1932) |
| [14] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
Comments
For the various kinds of bases mentioned in the article see Basis and [a2].
References
| [a1] | J. Weidmann, "Linear operators in Hilbert spaces" , Springer (1980) |
| [a2] | I.M. Singer, "Bases in Banach spaces" , 1–2 , Springer (1970–1981) |
Hilbert space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert_space&oldid=12159