Difference between revisions of "Group completion theorem"
From Encyclopedia of Mathematics
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | g1102601.png | ||
| + | $#A+1 = 6 n = 3 | ||
| + | $#C+1 = 6 : ~/encyclopedia/old_files/data/G110/G.1100260 Group completion theorem | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''in algebraic topology'' | ''in algebraic topology'' | ||
| − | Let | + | Let $ M $ |
| + | be a topological [[Monoid|monoid]] and $ BM $ | ||
| + | its classifying space. Let $ M \rightarrow \Omega BM $ | ||
| + | be the canonical mapping. Then $ H _ {*} ( M ) \rightarrow H _ {*} ( \Omega BM ) $ | ||
| + | induces an isomorphism | ||
| − | + | $$ | |
| + | H _ {*} ( M ) [ \pi _ {0} ( M ) ^ {- 1 } ] \rightarrow H _ {*} ( \Omega BM ) . | ||
| + | $$ | ||
| − | This theorem plays an important role in [[K-theory| | + | This theorem plays an important role in [[K-theory| $ K $- |
| + | theory]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. McDuff, G. Segal, "Homology fibrations and the "group completion" theorem" ''Invent. Math.'' , '''31''' (1976) pp. 279–287</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.F. Jardine, "The homotopical foundations of algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110260/g1102607.png" />-theory" , ''Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110260/g1102608.png" />-Theory and Algebraic Number Theory'' , ''Contemp. Math.'' , '''83''' , Amer. Math. Soc. (1989) pp. 57–82 {{MR|991976}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.P. May, "Classifying spaces and fibrations" , ''Memoirs'' , '''155''' , Amer. Math. Soc. (1975) {{MR|0370579}} {{ZBL|0321.55033}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M.B. Barrat, S.B. Priddy, "On the homology of non-connected monoids and their associated groups" ''Comm. Math. Helvetici'' , '''47''' (1972) pp. 1–14 {{MR|314940}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> I. Moerdijk, "Bisimplicial sets and the group-completion theorem" , ''Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110260/g1102609.png" />-Theory: Connections with Geometry and Topology'' , Kluwer Acad. Publ. (1989) pp. 225–240 {{MR|1045852}} {{ZBL|0708.18008}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. McDuff, G. Segal, "Homology fibrations and the "group completion" theorem" ''Invent. Math.'' , '''31''' (1976) pp. 279–287</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.F. Jardine, "The homotopical foundations of algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110260/g1102607.png" />-theory" , ''Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110260/g1102608.png" />-Theory and Algebraic Number Theory'' , ''Contemp. Math.'' , '''83''' , Amer. Math. Soc. (1989) pp. 57–82 {{MR|991976}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.P. May, "Classifying spaces and fibrations" , ''Memoirs'' , '''155''' , Amer. Math. Soc. (1975) {{MR|0370579}} {{ZBL|0321.55033}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M.B. Barrat, S.B. Priddy, "On the homology of non-connected monoids and their associated groups" ''Comm. Math. Helvetici'' , '''47''' (1972) pp. 1–14 {{MR|314940}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> I. Moerdijk, "Bisimplicial sets and the group-completion theorem" , ''Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g110/g110260/g1102609.png" />-Theory: Connections with Geometry and Topology'' , Kluwer Acad. Publ. (1989) pp. 225–240 {{MR|1045852}} {{ZBL|0708.18008}} </TD></TR></table> | ||
Latest revision as of 19:42, 5 June 2020
in algebraic topology
Let $ M $ be a topological monoid and $ BM $ its classifying space. Let $ M \rightarrow \Omega BM $ be the canonical mapping. Then $ H _ {*} ( M ) \rightarrow H _ {*} ( \Omega BM ) $ induces an isomorphism
$$ H _ {*} ( M ) [ \pi _ {0} ( M ) ^ {- 1 } ] \rightarrow H _ {*} ( \Omega BM ) . $$
This theorem plays an important role in $ K $- theory.
References
| [a1] | D. McDuff, G. Segal, "Homology fibrations and the "group completion" theorem" Invent. Math. , 31 (1976) pp. 279–287 |
| [a2] | J.F. Jardine, "The homotopical foundations of algebraic 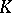 -theory" , Algebraic -theory" , Algebraic 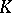 -Theory and Algebraic Number Theory , Contemp. Math. , 83 , Amer. Math. Soc. (1989) pp. 57–82 MR991976 -Theory and Algebraic Number Theory , Contemp. Math. , 83 , Amer. Math. Soc. (1989) pp. 57–82 MR991976 |
| [a3] | J.P. May, "Classifying spaces and fibrations" , Memoirs , 155 , Amer. Math. Soc. (1975) MR0370579 Zbl 0321.55033 |
| [a4] | M.B. Barrat, S.B. Priddy, "On the homology of non-connected monoids and their associated groups" Comm. Math. Helvetici , 47 (1972) pp. 1–14 MR314940 |
| [a5] | I. Moerdijk, "Bisimplicial sets and the group-completion theorem" , Algebraic 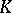 -Theory: Connections with Geometry and Topology , Kluwer Acad. Publ. (1989) pp. 225–240 MR1045852 Zbl 0708.18008 -Theory: Connections with Geometry and Topology , Kluwer Acad. Publ. (1989) pp. 225–240 MR1045852 Zbl 0708.18008 |
How to Cite This Entry:
Group completion theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Group_completion_theorem&oldid=24078
Group completion theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Group_completion_theorem&oldid=24078
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article