Geometry of immersed manifolds
A theory that deals with the extrinsic geometry and the relation between the extrinsic and intrinsic geometry (cf. also Interior geometry) of submanifolds in a Euclidean or Riemannian space. The geometry of immersed manifolds is a generalization of the classical differential geometry of surfaces in the Euclidean space 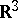 . The intrinsic and extrinsic geometries of an immersed manifold are usually described locally by means of the first and the second fundamental form, respectively. For immersions of an
. The intrinsic and extrinsic geometries of an immersed manifold are usually described locally by means of the first and the second fundamental form, respectively. For immersions of an 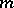 -dimensional manifold
-dimensional manifold 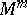 in a manifold
in a manifold 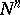 one has a concept of congruence (see Immersion of a manifold). In the geometry of immersed manifolds one examines properties that are identical for congruent immersions, i.e. properties of a surface
one has a concept of congruence (see Immersion of a manifold). In the geometry of immersed manifolds one examines properties that are identical for congruent immersions, i.e. properties of a surface 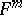 defined by an immersion
defined by an immersion 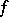 . In this connection, an immersion and a surface are not distinguished from the geometrical point of view. An immersion
. In this connection, an immersion and a surface are not distinguished from the geometrical point of view. An immersion 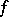 induces a mapping
induces a mapping 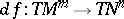 of the tangent bundles (cf. Tangent bundle).
of the tangent bundles (cf. Tangent bundle).
The first quadratic (fundamental) form 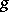 of a submanifold
of a submanifold 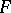 is defined on
is defined on  by
by
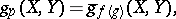 |
where  ,
, 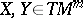 and
and 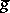 is a Riemannian metric on
is a Riemannian metric on 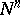 . Here and subsequently, the vectors
. Here and subsequently, the vectors 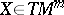 are not distinguished in symbols from their image
are not distinguished in symbols from their image 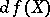 . The quadratic form
. The quadratic form  defines the structure of a Riemannian space
defines the structure of a Riemannian space 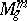 on
on 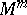 ; the properties of
; the properties of  constitute the subject of the intrinsic geometry of the submanifold
constitute the subject of the intrinsic geometry of the submanifold 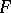 . If
. If 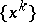 ,
, 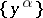 ,
, 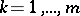 ,
, 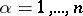 , are local coordinates in
, are local coordinates in 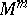 and
and 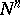 , the immersion
, the immersion 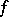 is given by the parametric equations
is given by the parametric equations 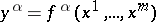 . In local coordinates
. In local coordinates
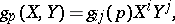 |
where 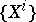 and
and 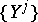 are the components of the vectors
are the components of the vectors 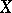 and
and 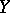 ,
,
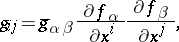 |
and  are the components of the metric tensor
are the components of the metric tensor 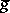 of the Riemannian space
of the Riemannian space 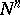 .
.
Concepts such as curve length, volume of a region, Levi-Civita connection 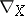 of the intrinsic metric, curvature transformation
of the intrinsic metric, curvature transformation 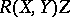 , etc., relate to the intrinsic geometry of
, etc., relate to the intrinsic geometry of 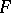 . The computational formulas applying here can be consulted in Riemannian geometry.
. The computational formulas applying here can be consulted in Riemannian geometry.
The second (fundamental) tensor (form)  is defined by
is defined by
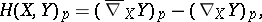 |
where  and
and  are the Levi-Civita connections in
are the Levi-Civita connections in 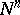 and
and 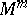 , respectively. In fact,
, respectively. In fact, 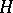 is not dependent on the vector fields
is not dependent on the vector fields 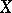 and
and 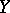 but only on their values at the point
but only on their values at the point  and is a bilinear symmetric mapping
and is a bilinear symmetric mapping
 |
where 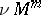 is the normal bundle of
is the normal bundle of 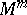 in
in 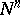 . For each unit vector
. For each unit vector 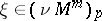 , the equations
, the equations
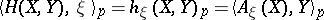 |
define the second quadratic form (or second fundamental form) 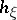 and the shape operator
and the shape operator 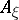 in the direction of
in the direction of  . In local coordinates the components
. In local coordinates the components  of the form
of the form 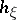 are
are
 |
where  are the components of
are the components of 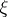 .
.
One defines the principal curvature, principal direction in the direction of  , and other related concepts for the form
, and other related concepts for the form  in the usual way (i.e. as for a surface in the Euclidean space
in the usual way (i.e. as for a surface in the Euclidean space 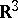 ).
).
Using elementary symmetric functions, one can construct various principal-curvature functions, such as, for example, the mean curvature
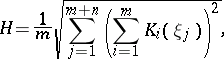 |
where 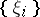 is an orthonormal set of normals and
is an orthonormal set of normals and 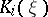 are the principal curvatures of the forms
are the principal curvatures of the forms 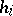 ; the Chern–Lashof curvature
; the Chern–Lashof curvature
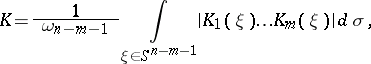 |
where  is the volume of the sphere
is the volume of the sphere 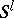 ; and also the length of the second fundamental form
; and also the length of the second fundamental form
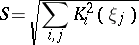 |
The values of the first and second fundamental forms for a submanifold at a point 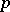 define it near
define it near 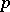 infinitesimally up to small quantities of the second order. Each
infinitesimally up to small quantities of the second order. Each 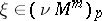 ,
, 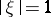 , corresponds to an osculating paraboloid (for a submanifold in a Euclidean space, this is the osculating paraboloid for the projection of the submanifold on the
, corresponds to an osculating paraboloid (for a submanifold in a Euclidean space, this is the osculating paraboloid for the projection of the submanifold on the 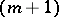 -dimensional plane defined by
-dimensional plane defined by 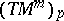 and
and 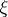 ). If
). If  (i.e. in the case of a hypersurface), the form
(i.e. in the case of a hypersurface), the form  is unique up to sign. In that case, the second fundamental tensor and the second fundamental form do not differ, and the theory acquires considerable similarity with the classical theory of surfaces in
is unique up to sign. In that case, the second fundamental tensor and the second fundamental form do not differ, and the theory acquires considerable similarity with the classical theory of surfaces in 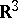 .
.
Basic equations.
The basic equations for an immersed manifold, i.e. the Gauss equations, the Codazzi–Mainardi equations and the Ricci equations, relate the first and second fundamental forms and the curvature tensors of  and
and 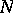 . For each vector field section
. For each vector field section 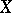 over
over 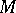 of the vector bundle
of the vector bundle 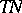 restricted to
restricted to 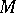 , let
, let  denote the tangential component and
denote the tangential component and 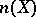 the normal component. The Gauss formula defining the second fundamental form,
the normal component. The Gauss formula defining the second fundamental form,
 |
gives the normal-tangent decomposition of  for
for 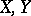 vector fields on
vector fields on 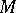 . The Weingarten formula (defining the shape operator),
. The Weingarten formula (defining the shape operator),
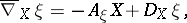 |
does the same in case  is a vector field on
is a vector field on 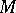 and the section
and the section  of
of 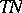 is normal to
is normal to  . In terms of the shape operators and the second fundamental form one finds that for three vector fields
. In terms of the shape operators and the second fundamental form one finds that for three vector fields 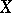 ,
, 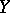 ,
, 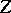 on
on 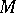 the tangential component of
the tangential component of 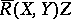 is equal to
is equal to
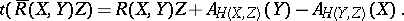 |
Taking a fourth vector field 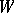 on
on 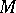 this leads to the Gauss equations
this leads to the Gauss equations
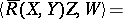 | (1) |
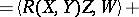 |
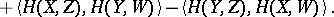 |
The normal component of 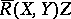 is equal to
is equal to
 | (2) |
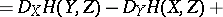 |
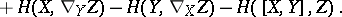 |
Define the connection  on the vector bundle
on the vector bundle 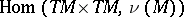 , where
, where 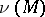 is the normal bundle to
is the normal bundle to 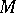 in
in 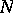 , by the formula
, by the formula
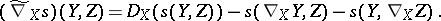 |
Then (2) can be rewritten as
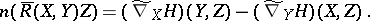 | (2prm) |
Equations (2) (or (2prm)) are the Codazzi–Mainardi equations (in intrinsic form) (cf. also Peterson–Codazzi equations).
Finally, consider the normal component of 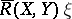 where
where 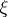 is a section of
is a section of 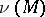 (by the symmetry properties of
(by the symmetry properties of  the horizontal component follows from the Codazzi–Mainardi equations). One has
the horizontal component follows from the Codazzi–Mainardi equations). One has
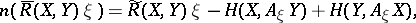 | (3) |
the Ricci equations. Here 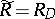 is the curvature tensor of the connection
is the curvature tensor of the connection 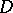 on the normal bundle
on the normal bundle 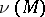 . The Gauss, Codazzi–Mainardi and Ricci equations are the only general equations available for an isometric immersion. It is reasonable to expect something interesting for
. The Gauss, Codazzi–Mainardi and Ricci equations are the only general equations available for an isometric immersion. It is reasonable to expect something interesting for 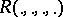 if three of the fields are normal. Indeed,
if three of the fields are normal. Indeed, 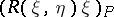 then has nothing to do with the immersed manifold
then has nothing to do with the immersed manifold 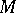 at the point
at the point 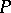 (except with the point
(except with the point 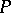 itself).
itself).
If the ambient manifold 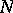 is of constant curvature
is of constant curvature 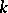 , then
, then 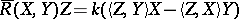 and so
and so 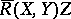 is tangent to
is tangent to 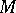 . The Gauss, Ricci and Codazzi–Mainardi equations reduce to
. The Gauss, Ricci and Codazzi–Mainardi equations reduce to
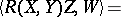 | (4) |
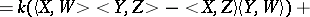 |
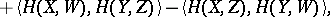 |
 | (5) |
where 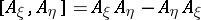 , and
, and
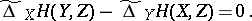 | (6) |
These equations make sense in a more general setting. Indeed, let 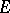 be a Riemannian vector bundle over
be a Riemannian vector bundle over 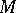 , i.e. there is a (bundle) Riemannian metric
, i.e. there is a (bundle) Riemannian metric 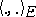 on
on 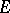 , and let there be a Riemannian connection
, and let there be a Riemannian connection 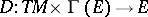 , where
, where 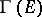 denotes the space of smooth sections of
denotes the space of smooth sections of 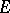 , which is adapted to the metric. This last phrase means that
, which is adapted to the metric. This last phrase means that 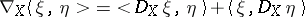 . A bilinear mapping
. A bilinear mapping 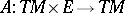 such that
such that 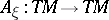 is self-adjoint for all
is self-adjoint for all  is called a second fundamental tensor in
is called a second fundamental tensor in 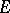 . The associated second fundamental form in
. The associated second fundamental form in  is then defined by
is then defined by
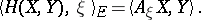 |
The three equations (4), (5), (6) make perfect sense in this more general setting. One has now the following generalization of the Bonnet theorem [2]: Let 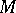 be a simply-connected Riemannian manifold equipped with a Riemannian vector bundle of dimension
be a simply-connected Riemannian manifold equipped with a Riemannian vector bundle of dimension  with a compatible connection
with a compatible connection 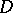 , second fundamental tensor
, second fundamental tensor 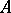 and associated second fundamental form
and associated second fundamental form 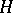 . Suppose that equations (4), (5), (6) hold. Then there is an isometric immersion of
. Suppose that equations (4), (5), (6) hold. Then there is an isometric immersion of 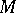 into a simply-connected Riemannian manifold of constant curvature
into a simply-connected Riemannian manifold of constant curvature 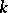 (a space form) and dimension
(a space form) and dimension  such that the normal bundle is
such that the normal bundle is 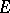 .
.
This immersion is unique in the following sense. Let 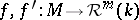 be two isometric immersions of
be two isometric immersions of 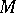 into a space form
into a space form 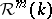 of curvature
of curvature 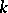 and with normal bundles
and with normal bundles 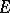 and
and 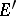 , with their induced bundle metrics, second fundamental forms and connections. Suppose that there is a bundle mapping
, with their induced bundle metrics, second fundamental forms and connections. Suppose that there is a bundle mapping 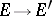 ,
,
 |
covering an isometry 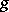 of
of 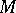 and such that
and such that 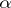 preserves the bundle metrics, connections and second fundamental forms. Then there is a rigid motion
preserves the bundle metrics, connections and second fundamental forms. Then there is a rigid motion  of
of 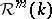 such that
such that 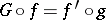 .
.
Immersion classes.
The geometry of higher-dimensional immersed manifolds arose and developed a long time ago from the theory of the existence of isometric immersions of Riemannian manifolds in 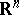 , or less often in a space of constant curvature
, or less often in a space of constant curvature  (see Isometric immersion). Concerning extrinsic geometrical properties and the links between the extrinsic and the intrinsic geometry of surfaces, two-dimensional surfaces in
(see Isometric immersion). Concerning extrinsic geometrical properties and the links between the extrinsic and the intrinsic geometry of surfaces, two-dimensional surfaces in 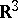 only have been examined in detail. In that case there exists a classification of the points on the surface, leading for two-dimensional surfaces to the classes of convex surfaces, saddle surfaces and developable surfaces. Among others, these classes are basic objects of research in differential geometry in the large. In the higher-dimensional case, no such classification of points on a surface is known (1983). Only certain classes of higher-dimensional surfaces are known:
only have been examined in detail. In that case there exists a classification of the points on the surface, leading for two-dimensional surfaces to the classes of convex surfaces, saddle surfaces and developable surfaces. Among others, these classes are basic objects of research in differential geometry in the large. In the higher-dimensional case, no such classification of points on a surface is known (1983). Only certain classes of higher-dimensional surfaces are known: 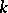 -convex,
-convex, 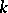 -saddle,
-saddle, 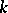 -developable surfaces.
-developable surfaces.
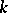 -convex surfaces.
-convex surfaces.
A surface 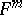 in
in 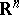 is called
is called 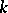 -convex if for each point
-convex if for each point 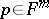 there exists a normal
there exists a normal 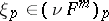 for which
for which 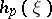 is positive definite, and if for any
is positive definite, and if for any 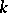 -dimensional direction
-dimensional direction 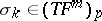 ,
, 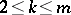 , one can find on
, one can find on 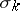 a two-dimensional direction
a two-dimensional direction 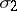 such that
such that 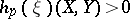 (or
(or  ) for each
) for each 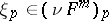 for
for 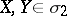 ,
,  . A two-convex surface
. A two-convex surface 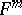 in
in 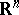 is a convex hypersurface in some
is a convex hypersurface in some 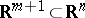 [4]. The intrinsic metric of a
[4]. The intrinsic metric of a 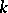 -convex surface has the following property: At each point
-convex surface has the following property: At each point 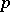 and for each
and for each 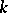 -dimensional direction
-dimensional direction 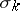 in the tangent space one can find a two-dimensional direction
in the tangent space one can find a two-dimensional direction  in which the Riemannian curvature is strictly positive.
in which the Riemannian curvature is strictly positive.
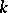 -saddle surfaces.
-saddle surfaces.
A surface 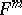 in
in  is called
is called 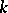 -saddle if for each point
-saddle if for each point 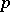 and for each normal
and for each normal 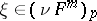 the number of eigen values of
the number of eigen values of 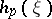 of one fixed sign does not exceed
of one fixed sign does not exceed 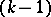 ,
, 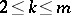 . A two-dimensional
. A two-dimensional 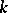 -saddle surface is an ordinary saddle surface in
-saddle surface is an ordinary saddle surface in 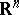 from which one cannot cut off the saddle point with a hyperplane. The intrinsic metric of a
from which one cannot cut off the saddle point with a hyperplane. The intrinsic metric of a 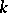 -saddle surface has the following property: At each point
-saddle surface has the following property: At each point 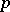 for each
for each 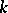 -dimensional direction
-dimensional direction  in the tangent space there is a two-dimensional direction
in the tangent space there is a two-dimensional direction 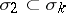 in which the Riemannian curvature is not positive. If a
in which the Riemannian curvature is not positive. If a 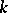 -saddle surface is complete in
-saddle surface is complete in 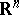 , then its homology
, then its homology 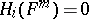 for
for 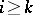 [4], [5]. A complete
[4], [5]. A complete 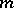 -dimensional
-dimensional 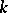 -saddle surface
-saddle surface 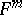 with non-negative Ricci curvature is a cylinder with generator of dimension
with non-negative Ricci curvature is a cylinder with generator of dimension 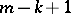 .
.
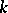 -developable (
-developable (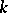 -parabolic) surfaces.
-parabolic) surfaces.
A surface 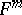 in
in 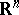 is called
is called 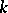 -developable if for each point
-developable if for each point 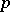 there exists a
there exists a 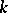 -dimensional direction
-dimensional direction 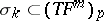 that consists of eigen vectors belonging to the zero eigen value of the second fundamental form with respect to each normal at the given point. The intrinsic metric of a
that consists of eigen vectors belonging to the zero eigen value of the second fundamental form with respect to each normal at the given point. The intrinsic metric of a  -developable surface has the following property: At each point
-developable surface has the following property: At each point 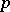 one can find a
one can find a 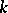 -dimensional subspace
-dimensional subspace 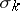 of the tangent space
of the tangent space 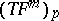 such that
such that 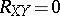 for any vector
for any vector 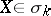 , where
, where  is any vector in the tangent space and
is any vector in the tangent space and  is the curvature operator. If a
is the curvature operator. If a 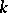 -developable surface
-developable surface 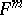 is complete in
is complete in 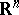 and carries an intrinsic metric of non-positive Ricci curvature, then it is a cylinder with a
and carries an intrinsic metric of non-positive Ricci curvature, then it is a cylinder with a 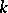 -dimensional generator .
-dimensional generator .
Free immersions.
If the image of 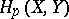 has maximum possible dimension
has maximum possible dimension 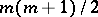 at each point
at each point 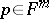 , then the immersion is called free. In that case, the first and second derivatives of the radius vector of the immersion
, then the immersion is called free. In that case, the first and second derivatives of the radius vector of the immersion  form a linearly independent system. In the class of free immersions there exist isometric immersions of dimension
form a linearly independent system. In the class of free immersions there exist isometric immersions of dimension 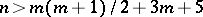 , giving rise to a complete loss of the connection between the intrinsic and the extrinsic geometry. For example, two free isometric immersions of an
, giving rise to a complete loss of the connection between the intrinsic and the extrinsic geometry. For example, two free isometric immersions of an 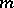 -dimensional manifold
-dimensional manifold 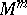 in
in 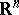 ,
, 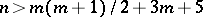 , may be connected by a homotopy consisting of free isometric immersions of
, may be connected by a homotopy consisting of free isometric immersions of 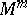 [7].
[7].
Immersions with small codimension.
If the codimension 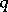 of an immersion is small, then it follows from the conditions on the intrinsic metric of the manifold that there must be restrictions on the second fundamental form of the surface. Also, the properties of the second fundamental form enable one to derive topological and extrinsic geometrical properties for the surface. In particular, one obtains non-immersibility theorems. For example, if an
of an immersion is small, then it follows from the conditions on the intrinsic metric of the manifold that there must be restrictions on the second fundamental form of the surface. Also, the properties of the second fundamental form enable one to derive topological and extrinsic geometrical properties for the surface. In particular, one obtains non-immersibility theorems. For example, if an 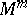 with sectional curvature
with sectional curvature  is isometrically immersed in
is isometrically immersed in 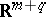 with
with 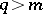 , then
, then 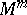 is a
is a  -saddle surface and its homology (in the case of completeness)
-saddle surface and its homology (in the case of completeness) 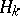 vanishes for
vanishes for 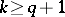 [5]. In particular, a compact
[5]. In particular, a compact 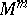 with
with  cannot be immersed in
cannot be immersed in 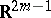 [8], [9]. If on the other hand
[8], [9]. If on the other hand 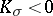 , then
, then 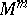 is not even locally immersible in
is not even locally immersible in 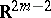 [9]. Similarly, an
[9]. Similarly, an 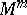 with
with 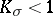 is not immersible in the sphere
is not immersible in the sphere 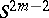 of radius 1. A compact
of radius 1. A compact 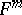 in
in 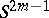 has Euler characteristic zero and a compact parallelizable covering manifold if
has Euler characteristic zero and a compact parallelizable covering manifold if 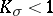 [10]. Regarding a surface
[10]. Regarding a surface  in
in 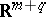 for
for 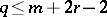 and
and 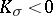 , it is known that its normal Pontryagin classes (cf. Pontryagin class) satisfy the conditions
, it is known that its normal Pontryagin classes (cf. Pontryagin class) satisfy the conditions
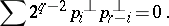 |
If 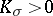 , it follows from
, it follows from 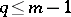 that
that 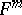 is a
is a 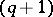 -convex surface [9]. In particular, for
-convex surface [9]. In particular, for 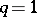 it is a two-convex surface. If
it is a two-convex surface. If 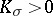 and
and 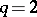 , a compact surface
, a compact surface 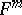 with
with 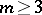 has the homologies of a sphere [11]. If
has the homologies of a sphere [11]. If 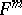 in
in 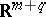 has non-positive sectional curvature, then it is an
has non-positive sectional curvature, then it is an 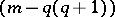 -developable surface and, in the case of completeness,
-developable surface and, in the case of completeness,  is a cylinder with generator of dimension
is a cylinder with generator of dimension  [10]. If, on the other hand,
[10]. If, on the other hand,  and
and 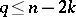 , the immersion of the manifold
, the immersion of the manifold 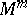 in
in 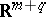 is a
is a 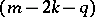 -developable surface [8], and in the case of completeness
-developable surface [8], and in the case of completeness  is a cylinder with generator of dimension
is a cylinder with generator of dimension 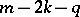 . Under more general assumptions, a compact surface
. Under more general assumptions, a compact surface
 |
is a product of hypersurfaces [12].
References
| [1] | L.P. Eisenhart, "Riemannian geometry" , Princeton Univ. Press (1949) |
| [2] | B.-Y. Chen, "Geometry of submanifolds" , M. Dekker (1973) |
| [3] | S.-S. Chern, R.K. Lashof, "On the total curvature of immersed manifolds" Amer. J. Math. , 79 (1957) pp. 306–318 |
| [4] | S.Z. Shefel', "Two classes of 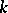 -dimensional surfaces in -dimensional surfaces in  -dimensional Euclidean space" Sib. Math. J. , 10 (1969) pp. 328–333 Sibirsk. Mat. Zh. , 10 : 2 (1969) pp. 459–466 -dimensional Euclidean space" Sib. Math. J. , 10 (1969) pp. 328–333 Sibirsk. Mat. Zh. , 10 : 2 (1969) pp. 459–466 |
| [5] | V.V. Glazyrin, "Topological and metric properties of 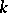 -saddle surfaces" Soviet Math. Dokl. , 18 (1977) pp. 532–534 Dokl. Akad. Nauk SSSR , 233 : 6 (1977) pp. 1028–1030 -saddle surfaces" Soviet Math. Dokl. , 18 (1977) pp. 532–534 Dokl. Akad. Nauk SSSR , 233 : 6 (1977) pp. 1028–1030 |
| [6a] | P. Hartman, "On isometric immersions in Euclidean space of manifolds with non-negative sectional curvatures" Trans. Amer. Math. Soc. , 115 (1965) pp. 94–109 |
| [6b] | P. Hartman, "On the isometric immersions in Euclidean space of manifolds with nonnegative sectional curvatures II" Trans. Amer. Math. Soc. , 147 (1970) pp. 529–540 |
| [7] | M.L. Gromov, "Isometric imbeddings and immersions" Soviet Math. Dokl. , 11 (1970) pp. 794–797 Dokl. Akad. Nauk SSSR , 192 : 6 (1970) pp. 1206–1209 |
| [8] | S.-S. Chern, N.H. Kuiper, "Some theorems on the isometric imbedding of compact Riemann manifolds in Euclidean space" Ann. of Math. , 56 : 3 (1952) pp. 422–430 |
| [9] | Yu.E. Borovskii, S.Z. Shefel', "On Chern–Kuiper theorem" Sib. Math. J. , 19 (1978) pp. 978 Sibirsk. Mat. Zh. , 19 : 6 (1978) pp. 1386–1387 |
| [10] | A.A. Borisenko, "Complete 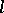 -dimensional surfaces of nonpositive extrinsic curvature in a Riemannian space" Math. USSR Sb. , 33 (1977) pp. 485–499 Mat. Sb. , 104 : 4 (1977) pp. 559–576 -dimensional surfaces of nonpositive extrinsic curvature in a Riemannian space" Math. USSR Sb. , 33 (1977) pp. 485–499 Mat. Sb. , 104 : 4 (1977) pp. 559–576 |
| [11] | J.D. Moore, "Codimension two submanifolds of positive curvature" Proc. Amer. Math. Soc. , 70 : 1 (1978) pp. 72–74 |
| [12] | R.B. Gardner, "New viewpoints in the geometry of submanifolds of 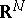 " Bull. Amer. Math. Soc. , 83 : 1 (1977) pp. 1–35 " Bull. Amer. Math. Soc. , 83 : 1 (1977) pp. 1–35 |
Comments
The mean curvature is the length of the mean curvature normal which is given by the trace of the bilinear (normal vector-valued) form 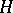 with respect to the first fundamental form. Minimal immersions are defined by the property that the mean curvature normal vanishes identically. They locally solve the least area problem.
with respect to the first fundamental form. Minimal immersions are defined by the property that the mean curvature normal vanishes identically. They locally solve the least area problem.
The integrand of the Chern–Lashof curvature is the absolute value of the Lipschitz–Killing curvature. The well-known Chern–Lashof theorem states that the Chern–Lashof curvature is at least 2 for compact immersed submanifolds of Euclidean spaces, and the value 2 is obtained just for convex hyperspheres of affine subspaces of suitable dimensions.
References
| [a1] | M. Gromov, "Partial differential relations" , Springer (1986) (Translated from Russian) |
| [a2] | M. Gromov, V. Rokhlin, "Embeddings and immersions in Riemannian geometry" Russian Math. Surveys , 25 : 5 (1970) pp. 1–57 Uspekhi Mat. Nauk , 25 : 5 (1970) pp. 3–62 |
Geometry of immersed manifolds. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Geometry_of_immersed_manifolds&oldid=12817