Gâteaux differential
From Encyclopedia of Mathematics
of a mapping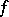 
of a linear topological space 
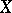into a linear topological space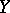 
The function
 |
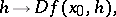where
 |
 |
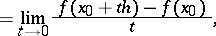on the assumption that the limit exists for all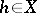 
, the convergence being understood in the topology of 
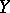. The Gâteaux differential thus defined is homogeneous, but is not additive. Gâteaux differentials of higher orders are defined in a similar manner. The mapping 
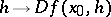is sometimes known as the Gâteaux variation or as the weak differential. See also Differentiation of a mapping; Variation.
Linearity and continuity are usually additionally stipulated: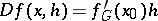 
, 
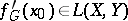. In such a case 
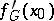is known as the Gâteaux derivative. If the mapping 
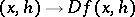is uniformly continuous in 
and continuous in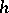 
in some domain, then the Fréchet derivative 
of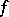 
exists in this domain and 
.
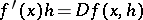References
| [1] | W.I. [V.I. Sobolev] Sobolew, "Elemente der Funktionalanalysis" , H. Deutsch , Frankfurt a.M. (1979) (Translated from Russian) |
| [2] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
Comments
References
| [a1] | M.S. Berger, "Nonlinearity and functional analysis" , Acad. Press (1977) |
How to Cite This Entry:
Gâteaux differential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=G%C3%A2teaux_differential&oldid=13805
Gâteaux differential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=G%C3%A2teaux_differential&oldid=13805
This article was adapted from an original article by V.M. Tikhomirov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article