Gâteaux derivative
From Encyclopedia of Mathematics
weak derivative
The derivative of a functional or a mapping which — together with the Fréchet derivative (the strong derivative) — is most frequently used in infinite-dimensional analysis. The Gâteaux derivative at a point 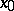 of a mapping
of a mapping  from a linear topological space
from a linear topological space 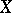 into a linear topological space
into a linear topological space 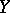 is the continuous linear mapping
is the continuous linear mapping 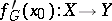 that satisfies the condition
that satisfies the condition
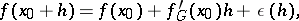 |
where 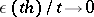 as
as 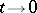 in the topology of
in the topology of 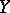 (see also Gâteaux variation). If the mapping
(see also Gâteaux variation). If the mapping 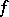 has a Gâteaux derivative at the point
has a Gâteaux derivative at the point 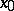 , it is called Gâteaux differentiable. The theorem on differentiation of a composite function is usually invalid for the Gâteaux derivative. See also Differentiation of a mapping.
, it is called Gâteaux differentiable. The theorem on differentiation of a composite function is usually invalid for the Gâteaux derivative. See also Differentiation of a mapping.
References
| [1] | R. Gâteaux, "Sur les fonctionnelles continues et les fonctionnelles analytiques" C.R. Acad. Sci. Paris Sér. I Math. , 157 (1913) pp. 325–327 |
| [2] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [3] | W.I. [V.I. Sobolev] Sobolew, "Elemente der Funktionalanalysis" , H. Deutsch , Frankfurt a.M. (1979) (Translated from Russian) |
| [4] | V.I. Averbukh, O.G. Smolyanov, "Theory of differentiation in linear topological spaces" Russian Math. Surveys , 22 : 6 (1967) pp. 201–258 Uspekhi Mat. Nauk , 22 : 6 (1967) pp. 201–260 |
Comments
References
| [a1] | M.S. Berger, "Nonlinearity and functional analysis" , Acad. Press (1977) |
How to Cite This Entry:
Gâteaux derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=G%C3%A2teaux_derivative&oldid=13686
Gâteaux derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=G%C3%A2teaux_derivative&oldid=13686
This article was adapted from an original article by V.M. Tikhomirov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article