Functions of a real variable, theory of
An area of mathematical analysis in which one studies questions of representation and approximation of functions, and their local and global properties. The modern theory of functions of a real variable typically involves a wide application of set-theoretic methods, along, naturally, with classical methods.
Thus, the object studied in the theory of functions of a real variable is a function. About this concept N.N. Luzin [3] wrote "It did not take shape all at once, but, having arisen two hundred years ago in the famous argument about a vibrating string, underwent deep changes even in the energetic polemics that started then. From then on there has been a constant deepening and evolution of this concept, continuing up to the present day. Therefore no single isolated formal definition can embrace the whole content of this concept …" . In accordance with this, it is completely natural to attribute the sources of the origin of the theory to the time of the argument about a vibrating string (L. Euler, D. Bernoulli, J. d'Alembert, J.L. Lagrange, and others), although the formation of this theory took place in the 19th century (J. Fourier, A.L. Cauchy, N.I. Lobachevskii, P. Dirichlet, B. Riemann, P.L. Chebyshev, C. Jordan, and others).
In classical analysis one studied mainly functions with a definite degree of smoothness. But in the second half of the 19th century certain problems took clear shape, waiting for a solution and touching on more general classes of functions, and also on a deeper study even of smooth functions. Among such problems one must put those of the measure of a set, the length of curves and the area of surfaces, the primitive and the integral, the relationship between integration and differentiation, the term-by-term integration and differentiation of series, the properties of functions obtained as a result of a limiting process, etc. The solution of these problems was of fundamental significance for mathematics. The classical methods of analysis could no longer give a sufficiently satisfactory answer to questions of this kind. In this connection there arose at the end of the 19th century an urgent need for a new critical review of the foundations of mathematical analysis, which was carried out at the end of the 19th century and beginning of the 20th century on the basis of set theory, with which the creation of the foundations of the modern theory of functions of a real variable was completed.
Usually the modern theory of functions of a real variable is divided into three parts: 1) the descriptive theory; 2) the metric theory; and 3) approximation theory.
The first two parts are particularly close, their foundations having been laid by E. Borel, R. Baire, H. Lebesgue, and others.
1) In the descriptive theory of functions one studies the properties of certain classes of functions that are obtained as a result of limiting processes. This study (on the basis of, and in connection with, descriptive set theory) has shown that the concept of a function is extremely complex. In this direction, Baire classes of functions were invented, which turned out to be most closely connected with the classification of Borel sets (cf. Borel set).
The fundamental results in the descriptive theory of sets and functions were obtained in the Soviet Union in the second and third decades of the 20th century (Luzin, M.Ya. Suslin, P.S. Aleksandrov, A.N. Kolmogorov, L.V. Keldysh, P.S. Novikov, and others).
2) In the metric theory of functions one studies the properties of functions on the basis of the concept of the measure of a set. The modern concept of the measure of a set (the Lebesgue measure) was introduced by Lebesgue in 1902. At the same time, on the basis of this concept, he also created the theory of the integral (the Lebesgue integral). These two extremely important concepts — measure and integral — form the foundation of the metric theory of functions, which is concerned with the study of properties of functions, derivatives, integrals, series of functions, etc.
The first major results in the Soviet Union in this direction were obtained in the second decade of the 20th century by D.F. Egorov and Luzin (see Egorov theorem; Luzin 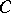 -property). The founder and leader of the school of the metric theory of functions in the USSR was Luzin.
-property). The founder and leader of the school of the metric theory of functions in the USSR was Luzin.
To the metric theory of functions should be assigned the theory of summation of series and sequences, and also the theory of almost-periodic functions (cf. Almost-periodic function). This last theory was created in the work of P. Bohl, H. Bohr, N.N. Bogolyubov, H. Weyl, V.V. Stepanova, and others.
Research on the metric theory of functions and the concepts and methods that have arisen in it have had a particularly large influence on various areas of modern mathematics. Indeed: in much analytical research in several branches of mathematics one can seldom manage without the Lebesgue measure and the Lebesgue integral (or their respective analogues and generalizations).
3) The foundations of the theory of approximation of functions of a real variable were laid in the classical papers of Chebyshev (mid 19th century). He introduced the extremely important concept of the best approximation 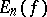 , and proved one of the basic theorems about the best approximation of functions by polynomials (the Chebyshev theorem). The further development of this theory was carried out principally in the Soviet Union — in the work of E.I. Zolotarev, A.N. Korkin and the brothers A.A. and V.A. Markov. A large role in approximation theory was played by the Weierstrass theorem on the possibility of approximating continuous functions by polynomials.
, and proved one of the basic theorems about the best approximation of functions by polynomials (the Chebyshev theorem). The further development of this theory was carried out principally in the Soviet Union — in the work of E.I. Zolotarev, A.N. Korkin and the brothers A.A. and V.A. Markov. A large role in approximation theory was played by the Weierstrass theorem on the possibility of approximating continuous functions by polynomials.
At the beginning of the 20th century it was discovered that the differentiability properties of functions have an influence on the rate at which 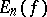 tends to zero as
tends to zero as 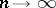 (Lebesgue, Borel, Ch.J. de la Vallée-Poussin).
(Lebesgue, Borel, Ch.J. de la Vallée-Poussin).
The most important problems relating to the elucidation of the links between the structural properties of functions and the rate of their approximation by polynomials were solved by S.N. Bernshtein [S.N. Bernstein] and D. Jackson (cf. Bernstein theorem; Jackson theorem).
Starting from the 1930's, the research in the USSR on the approximation theory of functions of a real variable took a particularly wide scope. Along with the research of Bernshtein, in the first place the extensive achievements of Kolmogorov and S.M. Nikol'skii, and of their pupils, should be mentioned here (cf. Imbedding theorems).
References
| [1] | R. Baire, "Leçons sur les fonctions discontinues, professées au collège de France" , Gauthier-Villars (1905) |
| [2] | N.N. [N.N. Luzin] Lusin, "Leçons sur les ensembles analytiques et leurs applications" , Gauthier-Villars (1930) |
| [3] | N.N. Luzin, , Collected works , 3 , Moscow (1959) pp. 319–341 (In Russian) |
| [4] | A.M. Lyapunov, S.P. Novikov, "Descriptive set theory" , B Mathematics in the USSR during thirty years: 1917–1947 , Moscow-Leningrad (1948) (In Russian) |
| [5] | H. Lebesgue, "Leçons sur l'intégration et la récherche des fonctions primitives" , Gauthier-Villars (1928) |
| [6] | E. Kamke, "Das Lebesgue–Stieltjes Integral" , Teubner (1960) |
| [7] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [8] | P.L. Ul'yanov, "The metric theory of functions" , The history of Soviet Mathematics , 3 , Kiev (1968) pp. 530–568 (In Russian) |
| [9] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [10] | H. Bohr, "Almost periodic functions" , Chelsea, reprint (1947) (Translated from German) |
| [11] | B.M. Levitan, "Almost-periodic functions" , Moscow (1953) (In Russian) |
| [12] | P.L. Chebyshev, "Questions on smallest quantities connected with the approximate representation of functions (1859)" , Collected works , 2 , Moscow-Leningrad (1947) pp. 151–235 (In Russian) |
| [13] | S.M. Lozinskii, I.P. Natanson, "Metric and constructive theory of functions of a real variable" , Mathematics in the USSR during 40 years: 1917–1957 , 1 , Moscow (1959) (In Russian) |
| [14] | S.M. Nikol'skii, "The theory of approximation of functions by polynomials" , The history of national mathematics , 3 , Kiev (1968) (In Russian) |
| [15] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) |
Comments
The decomposition into three main parts as done in the main article is a Russian one. For the first part see Descriptive set theory, [a2], [a3], [a4]. As to the second part, the phrase "metric theory of functions" is not used in Western literature, and the corresponding notions are spread out over various branches of functional analysis. Consult the various articles on approximation for the third part (see also [a5]). [a1] and [a6] are general references.
References
| [a1] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) |
| [a2] | H.L. Royden, "Real analysis" , Macmillan (1968) |
| [a3] | A.C.M. van Rooy, W.H. Schikhof, "A second course on real functions" , Cambridge Univ. Press (1982) |
| [a4] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) |
| [a5] | G.G. Lorentz, "Approximation of functions" , Holt, Rinehart & Winston (1966) |
| [a6] | G. Choquet, "Outils topologiques et métriques de l'analyse mathématique" , Centre Docum. Univ. Paris (1969) (Rédigé par C. Mayer) |
Functions of a real variable, theory of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Functions_of_a_real_variable,_theory_of&oldid=15169